Matlab RRT算法三维轨迹规划及贪心算法轨迹优化
RRT算法简单介绍
1. RRT算法定义
RRT(Rapidly-Exploring Random Tree)算法是一种基于采样的路径规划算法,常用于移动机器人路径规划,适合解决高维空间和复杂约束下的路径规划问题。基本思想是以产生随机点的方式通过一个步长向目标点搜索前进,有效躲避障碍物,避免路径陷入局部极小值,收敛速度快。本文通过matlab实现RRT算法,解决二维平面的路径规划问题。
2. RRT算法基本步骤
1)确定起点start和终止点goal;
2)在空间中随机生成新的点r(50%为随机点,50%为目标点,目的是增强RRT向goal点生成的导向性);
3)判断点r与轨迹树中哪一个节点的欧氏距离最小,记该点为最近父节点closetNode;
4)沿生长向量方向(最近父节点closetNode指向随机点r的方向)按照步长stepSize生成新的子节点newNode;
5)碰撞检测:检测closetNode到newNode的连线是否会与障碍物发生碰撞。若是,返回步骤2,重新生成随机点;若否,则将newNode添加到轨迹树中。
6)检测是否到达goal附近。若是,结束搜索;若否,返回步骤2继续搜索。
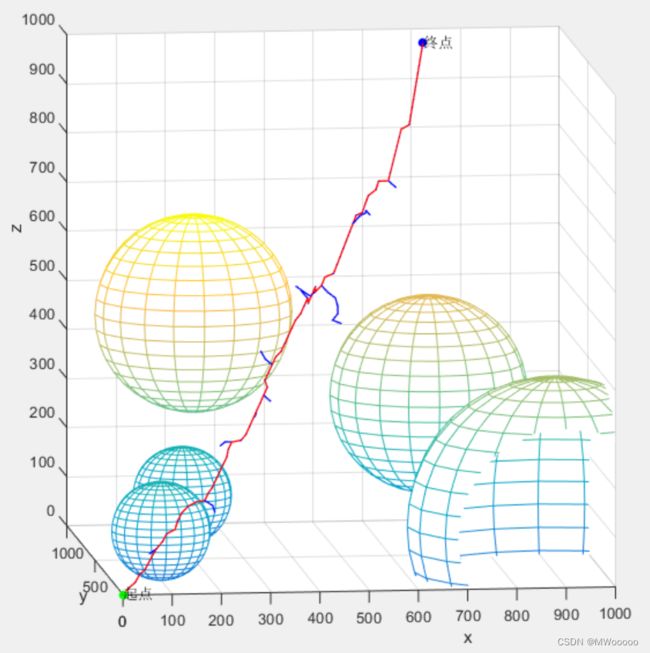
三维轨迹Matlab仿真效果:
障碍物我们只设置了球形障碍物,也可以设置成立方体、圆柱体等等。
实施效果1:
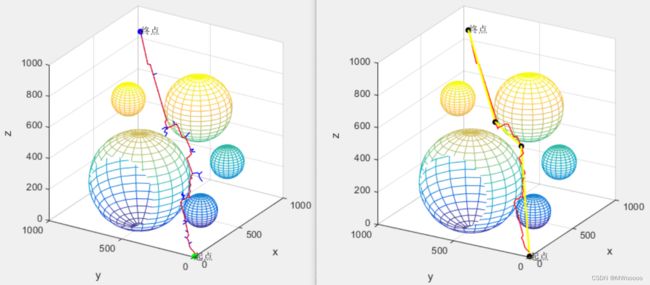
左:RRT随机树 右:贪心算法优化后的随机树
优化前,RRT树有80个节点,并且路径并不平滑。优化后,随机树只有三个点,路径只有两条直线组成。当然还可以继续对路径进行平滑,本文没有再继续做这些工作了。
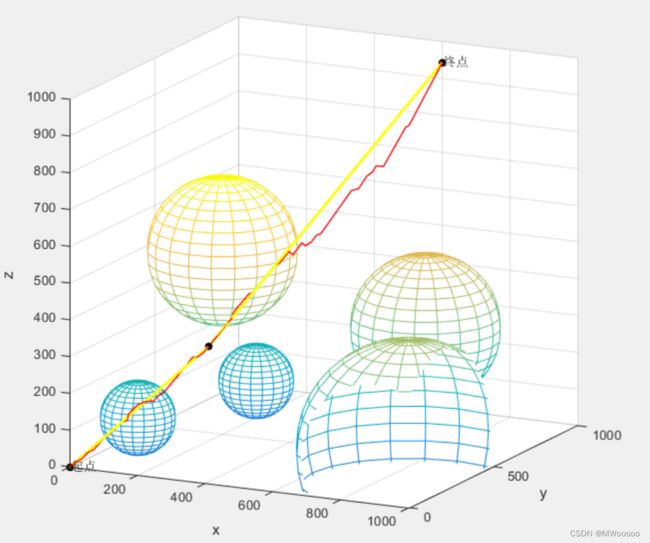
实施效果2:
以下为RRT算法的Matlab实现代码:
mian函数:
%created by MW
%date: 2022/5/25
%func: RRT avoiding obstacle
clc;
clear;
%% 创建并绘制障碍物
circleCenter = [100 200 100;
200 700 100;
200 500 500;
700 700 300;
900 200 100];
radius = [100;100;200;200;300];
%绘制球形障碍物
figure(1);
[x, y, z] = sphere; %创建一个坐标在原点,半径为1的标准圆,用于绘制自定义的圆
for i = 1: length(radius)
mesh(radius(i)*x + circleCenter(i,1), radius(i)*y + circleCenter(i,2), radius(i)*z + circleCenter(i,3));
hold on;
end
axis equal;
%% 创建初始位置和目标位置并绘制
start = [0 0 0];
goal = [700 800 1000];
hold on;
scatter3(start(1),start(2),start(3),'filled','g');
scatter3(goal(1),goal(2),goal(3),'filled','b');
%% 图片标注
text(start(1),start(2),start(3),'起点');
text(goal(1),goal(2),goal(3),'终点');
view(3);
grid on;
axis equal;
axis([0 1000 0 1000 0 1000]);
xlabel('x');
ylabel('y');
zlabel('z');
%% RRT方法生成避障轨迹
path = RRT(start,goal,radius,circleCenter);
%% 贪心算法优化RRT轨迹
newPath = GreedyOptimize(path,radius,circleCenter);
figure(2);
%绘制球形障碍物
[x, y, z] = sphere; %创建一个坐标在原点,半径为1的标准圆,用于绘制自定义的圆
for i = 1: length(radius)
mesh(radius(i)*x + circleCenter(i,1), radius(i)*y + circleCenter(i,2), radius(i)*z + circleCenter(i,3));
hold on;
end
axis equal;
%绘制原RRT树
plot3(path(:,1), path(:,2), path(:,3),'LineWidth',1,'Color','r');
%绘制优化后的RRT树
for k1 =1: length(newPath)
point = newPath(k1,:);
scatter3(point(1),point(2),point(3),'filled','k');
end
plot3(newPath(:,1), newPath(:,2), newPath(:,3),'LineWidth',2,'Color','y');
%图片标注
text(start(1),start(2),start(3),'起点');
text(goal(1),goal(2),goal(3),'终点');
view(3);
grid on;
axis equal;
axis([0 1000 0 1000 0 1000]);
xlabel('x');
ylabel('y');
zlabel('z');
RRT算法:
function path = RRT(start,goal,radius,circleCenter)
%% 定义RRT参数
stepSize = 20; %步长
maxIterTimes = 5000; %最大迭代步数
iterTime = 0; %当前迭代次数
threshold = 20; %阈值
searchSize = [1000 1000 1000]; %空间尺寸
RRTree = double([start -1]); %创建RRT树,共4列。前3列为节点坐标,第4列为当前节点的父节点的索引。初始点的索引为-1
%多个点到某一点欧式距离计算方法
calcDis = @(a,b) sqrt((b(:,1)-a(1,1)).^2 + (b(:,2)-a(1,2)).^2 + (b(:,3)-a(1,3)).^2);
%% 寻找RRT路径
tic % tic-toc函数,用于计时,记录完成整个RRT树的运行时间
pathFound = false; %标志物,记录是否正确找到避障路径
while iterTime <= maxIterTimes
iterTime = iterTime +1;
%step1 - 生成随机点
%为了提高RRT扩展的导向性,以50%的概率在空间中随机生成生成新的随机点,50%的概率以目标点为新的随机点
if rand < 0.5
sample = rand(1,3) .* searchSize + start;
else
sample = goal;
end
%step2 - 寻找树上最近父节点
[val,nearIndex] = min(calcDis(sample, RRTree(:,1:3)),[],1); %计算树上每个节点到随机点的欧氏距离,并返回最短距离的值和index
closestNode = RRTree(nearIndex,1:3);
%step3 - 沿生长向量方向按照步长生成新的子节点
growVec = sample - closestNode;
growVec = growVec/sqrt(sum(growVec.^2));
newPoint = closestNode + growVec*stepSize;
%step4 - 碰撞检测
feasible = collisionDetec(newPoint,closestNode,radius,circleCenter);
if ~feasible
continue; %如果发生碰撞,则重新寻找随机点
end
%为树添加新节点
RRTree = [RRTree;
newPoint nearIndex];
plot3([closestNode(1) newPoint(1)],[closestNode(2) newPoint(2)],[closestNode(3) newPoint(3)],'LineWidth',1,'Color','b');
pause(0.01);
%检测是否到达goal附近
if sqrt(sum((newPoint - goal).^2)) <= threshold
pathFound = true;
break; %如果节点已到达goal附近,则结束搜寻
end
end
%搜索结束后如果搜索失败,显示错误信息
if ~pathFound
disp('no path found. maximum attempts reached');
end
toc
%% 绘制回溯路径
path = goal;
lastNode = nearIndex; %父节点索引,这里的nearIndex是goal的父节点索引
while lastNode >= 0
path =[RRTree(lastNode,1:3); path]; %将当前节点的上一个节点添加进回溯路径中
lastNode = RRTree(lastNode, 4); %更新父节点索引
end
plot3(path(:,1), path(:,2), path(:,3),'LineWidth',1,'Color','r');
end
碰撞检测算法:
线段检测:
%新的生长向量是否发生碰撞
function feasible = collisionDetec(newPoint,closestNode,radius,circleCenter)
feasible = true;
checkVec = newPoint - closestNode; %检测向量
%将检测向量以0.5为步长等比均分为无数个检测点,检测每个检测点是否与球发生碰撞
for i = 0:0.5:sqrt(sum(checkVec.^2))
checkPoint = closestNode + i.*(checkVec/sqrt(sum(checkVec.^2))); %生成检测点
checkPointFeasible = pointCollisionCheck(checkPoint,radius,circleCenter);
if ~checkPointFeasible
feasible = false;
break;
end
end
end
点检测:
%监测点是否发生碰撞
function pointFeasible = pointCollisionCheck(checkPoint,radius,circleCenter)
pointFeasible = true;
for s = 1:length(radius)
if sqrt(sum((checkPoint - circleCenter(s,:)).^2)) <= radius(s)
pointFeasible = false;
break;
end
end
end
贪心算法简单介绍
1. 贪心算法定义:
贪心算法,是指在对问题求解时,总是做出再当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是某种意义上的局部最优解。
贪心算法没有固定算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。
2. 贪心算法基本步骤:
步骤1:从某个初始解出发;
步骤2:采用迭代的过程,当可以向目标前进一步时,就根据局部最优策略,得到一部分解,缩小问题规模;
步骤3:将所有解综合起来。
本问题下的贪心算法:
1)连接目标点和初始点。
2)检测是否发生碰撞。
3)若是,表明从初始点到该点中间不能被省略,沿目标点往上回溯到上一级父节点(上一级父节点更新为新的目标点),回到步骤1;若否,表明从初始点到该点中间的所有节点均可被省略,将该点添加到新的随机树中,并将该点更新为新的初始点,目标点复位到最后一个节点,回到步骤1.
4)检测直到start更新至goal结束。
function newPath = GreedyOptimize(path,radius,circleCenter)
startIndex = 1;
goalIndex = length(path(:,1));
detectTimes = length(path(:,1)) - 1; %检测次数
newPath = [path(startIndex,:)]; %添加初始位置
while detectTimes >0;
detectTimes = detectTimes-1;
start = path(startIndex,:);
goal = path(goalIndex,:);
%碰撞检测
feasible = collisionDetec(goal,start,radius,circleCenter);
if ~feasible
goalIndex = goalIndex - 1; %若碰撞,index减1,继续向上探索父节点
continue;
else
newPath = [newPath; goal]; %若未发生碰撞,表示找到一个最优节点,则从该节点往上的所有父节点均可省略,将该节点添加至路径中
detectTimes = length(path(:,1)) - goalIndex; %检测次数更位
startIndex = goalIndex; %将当前节点索引更新为新的树的起点
goalIndex = length(path(:,1)); %将终点索引复位
end
end
newPath = [newPath; path(end,:)]; %添加目标位置
end