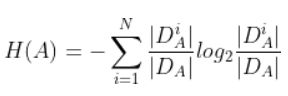机器学习实验二(决策树)
目录
一、原理
1.1决策树
1.2决策树的特点
1.3决策树的构造过程
1.4决策树的一般流程
1.4信息增益
1.5信息增益率
1.6基尼指数
二、划分数据集依据
2.1 信息增益(ID3),越大越好
2.2 信息增益率(C4.5)越大越好
2.3 Gini系数(CART)越小越好
三、三种方式实现预测博主粉丝
3.1 实验数据集
3.2
一、原理
1.1决策树
决策树(Decision Tree)是一种基本的分类与回归方法,在这里主要讨论用于分类的决策树。决策树的学习通常包含三个步骤:特征选择,决策树的生成,决策树的剪枝。
决策树是属于机器学习监督学习分类算法中比较简单的一种,决策树是一个预测模型;它代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。 是通过一系列规则对数据进行分类的过程。
1.2决策树的特点
- 优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
- 缺点:可能会产生过度匹配的问题。
- 适用数据类型:数值型和标称型(数值型需要离散化)。
1.3决策树的构造过程
一般包含三个部分
1、特征选择:特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准,如何选择特征有着很多不同量化评估标准标准,从而衍生出不同的决策树算法,如CART, ID3, C4.5等。
2、决策树生成: 根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则停止决策树停止生长。 树结构来说,递归结构是最容易理解的方式。
* 3、剪枝:决策树容易过拟合,一般来需要剪枝,缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。
1.4决策树的一般流程
(1)收集数据:可以使用任何方法。
(2)准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
(3)分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
(4)训练算法:构造树的数据结构。
(5)测试算法:使用经验树计算错误率。
(6)使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
1.4信息增益
划分数据集的大原则是:将无序的数据变得更加有序,但是各种方法都有各自的优缺点,信息论是量化处理信息的分支科学,在划分数据集前后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择,所以必须先学习如何计算信息增益,集合信息的度量方式称为香农熵,或者简称熵。
1.5信息增益率
与ID3不同之处就是:特征选择使用的是信息增益比,同时可以对连续属性进行处理。
(1) 用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足;
(2)在树构造过程中进行剪枝;
(3) 能够完成对连续属性的离散化处理;
(4) 能够对不完整数据进行处理。
1.6基尼指数
基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
注意: Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
二、划分数据集依据
2.1 信息增益(ID3)越大越好
D:数据集
A:特征A
K:类别的集合 k~K
(1)D的经验熵:
(表示数据集D的纯度,H越小,纯度越高)
(2)特征A将数据集D分成N个数据集,特征A对数据集D的经验条件熵:
(即给定特征A,计算每个子数据集的纯度再求和,表示给定A后数据集的纯度,数值越小纯度越高)
(3)特征A对数据集的信息增益:
(即特征A帮助提升的纯度的大小,值越大越好)
2.2 信息增益率(C4.5)越大越好
由于信息增益会偏向取值较多的特征(过拟合),解释:当特征A取值很多,则划分出的组数增多,使得H(D|A)减小,则信息增益增大。但是过于精细的划分,会使得分类失去意义。(比如按照身份证号给人分类,则每一个人都是一类)。
特征A对数据集D的信息增益率:
其中,特征A将数据集分成N类,则对于所有特征A相对应的数据的N个类的信息经验熵为(即表示了特征A为类别标签时,数据D的纯度):
因为当A将数据集D分成太多类时,其纯度降低,H(A)增加,相当于给信息增益添加了一项惩罚项。
2.3 Gini系数(CART)越小越好
基尼指数:从数据集里随机选取子项,度量其被错误分类到其他分组里的概率。基尼系数指数据的不纯度,越小越好。
CART是一个二叉树分类。
K是数据集D的标签集合:k~K
数据D的基尼系数:
若特征A将数据D分成两个数据集:
但是若当特征A将数据集D分成超过两个数据集时,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度Gini(D,Ai),(其中Ai 表示特征A的可能取值),然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分,这个划分的划分点,便是使用特征A对样本集合D进行划分的最佳划分点。
对各个概念的理解:熵描述了信息的不确定性,我们的目标是划分数据集D,使得划分后的数据集的不确定性降低。信息增益描述了特征A对于降低数据集D的不确定性的帮助,信息增益越大,说明A的引入增加了信息,降低了D的不确定性。然而,由于信息增益会偏向取值较多的特征,为了解决这个特征之间的选择不平衡的现象,我们添加了一项惩罚项,引入了信息增益率。
三者比较:
三、三种方式实现预测博主粉丝
3.1 实验数据集
| 是否关注该博主 是否三连 是粉丝 | |||
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
| 6 | 是 | 是 | 否 |
| 7 | 是 | 否 | 否 |
| 8 | 否 | 是 | 否 |
| 9 | 是 | 否 | 是 |
| 10 | 是 | 是 | 否 |
| 11 | 否 | 否 | 否 |
| 12 | 否 | 是 | 否 |
| 13 | 是 | 否 | 否 |
| 14 | 是 | 是 | 否 |
| 15 | 是 | 是 | 是 |
| 16 | 否 | 是 | 否 |
| 17 | 否 | 是 | 否 |
| 18 | 是 | 是 | 是 |
| 19 | 否 | 是 | 否 |
| 20 | 是 | 是 | 否 |
| 21 | 是 | 否 | 是 |
| 22 | 否 | 是 | 否 |
| 23 | 是 | 是 | 否 |
| 24 | 是 | 否 | 否 |
| 25 | 否 | 是 | 是 |
| 26 | 是 | 否 | 是 |
| 27 | 否 | 是 | 否 |
| 28 | 否 | 否 | 否 |
| 29 | 否 | 是 | 是 |
| 30 | 是 | 是 | 否 |
| 31 | 是 | 否 | 是 |
| 32 | 否 | 否 | 否 |
| 33 | 否 | 是 | 是 |
| 34 | 是 | 否 | 否 |
| 35 | 是 | 是 | 是 |
| 36 | 否 | 否 | 否 |
| 37 | 是 | 是 | 否 |
| 38 | 是 | 否 | 是 |
| 39 | 否 | 否 | 否 |
| 40 | 是 | 是 | 是 |
| 41 | 是 | 否 | 否 |
| 42 | 否 | 否 | 是 |
| 43 | 是 | 否 | 否 |
| 44 | 否 | 否 | 是 |
| 45 | 是 | 是 | 是 |
| 46 | 是 | 是 | 是 |
| 47 | 是 | 否 | 否 |
| 48 | 否 | 是 | 否 |
| 49 | 否 | 是 | 否 |
| 50 | 是 | 是 | 是 |
| 51 | 是 | 是 | 是 |
| 52 | 是 | 否 | 否 |
| 53 | 否 | 是 | 否 |
| 54 | 否 | 是 | 否 |
| 55 | 是 | 是 | 是 |
| 56 | 是 | 是 | 是 |
| 57 | 是 | 否 | 否 |
| 58 | 否 | 是 | 否 |
| 59 | 否 | 是 | 否 |
| 60 | 是 | 是 | 是 |
| 61 | 是 | 是 | 是 |
| 62 | 是 | 否 | 否 |
| 63 | 否 | 是 | 否 |
| 64 | 否 | 是 | 否 |
| 65 | 是 | 是 | 是 |
| 66 | 是 | 是 | 是 |
| 67 | 是 | 否 | 否 |
| 68 | 否 | 是 | 否 |
| 69 | 否 | 是 | 否 |
| 70 | 是 | 是 | 是 |
| 71 | 是 | 是 | 是 |
| 72 | 是 | 否 | 否 |
| 73 | 否 | 是 | 否 |
| 74 | 否 | 是 | 否 |
| 75 | 是 | 是 | 是 |
| 76 | 是 | 是 | 是 |
| 77 | 是 | 否 | 否 |
| 78 | 否 | 是 | 否 |
| 79 | 否 | 是 | 否 |
| 80 | 是 | 是 | 是 |
| 81 | 是 | 是 | 是 |
| 82 | 是 | 否 | 否 |
| 83 | 否 | 是 | 否 |
| 84 | 否 | 是 | 否 |
| 85 | 是 | 是 | 是 |
| 86 | 是 | 是 | 是 |
| 87 | 是 | 否 | 否 |
| 88 | 否 | 是 | 否 |
| 89 | 否 | 是 | 否 |
| 90 | 否 | 是 | 否 |
| 91 | 是 | 否 | 是 |
| 92 | 否 | 否 | 是 |
| 93 | 是 | 是 | 否 |
| 94 | 否 | 是 | 是 |
| 95 | 是 | 是 | 否 |
| 96 | 否 | 是 | 是 |
| 97 | 是 | 是 | 否 |
| 98 | 是 | 是 | 是 |
| 99 | 是 | 是 | 是 |
| 100 | 是 | 否 | 否 |
3.2
代码运行没有问题,但是在命令行下执行一直提示tree未定义,尝试下载sklearn也未能解决