[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)
这篇文章的主要成果:
1.提出了一种集合方法来生成对抗样本(感觉并不是本文的主要贡献,也不是特别有新意,就是把集合思想融入进了对抗样本)
2.正如论文的标题,作者深入分析了对抗样本的迁移性,并做了几何特性的分析,得出了一些比较有意思、且有点反直觉的结论。(几何部分真的太难懂了,人都看晕了)
注:这篇笔记中,蓝框里的是我对原文的一个简单的翻译,其余部分是我对文章的一些小的总结。
目录
- 0 摘要
- 1 简介
- 2 对抗深度学习及迁移性
-
- 2.1对抗深度学习问题
- 2.2:生成对抗样本的方法
-
- 2.2.1无目标方法
- 2.2.2有目标方法
- 2.3评估方法
- 3.无目标对抗样本
-
- 3.1 基于优化的方法
- 3.2快速梯度方法
- 3.3 加入随机扰动进行比较
- 4.有目标攻击
- 5.基于集合的方法
- 6.不同模型的几何特性
0 摘要
DNN的一个有趣的性质是对抗样本的存在,其可以在不同结构的模型中迁移。这些可迁移的对抗样本会严重阻碍DNN应用。过去的工作通常只利用小规模数据集研究迁移性。本文中,我们首次利用大规模数据集及大型模型来进行拓展研究,我们还是首个研究有目标对抗样本与其目标标签的迁移性。我们同时研究无目标攻击和有目标攻击,结果显示可迁移的无目标对抗样本很容易找,有目标攻击很难带着目标标签迁移。因此,我们提出了基于集成的方法来生成可迁移的对抗样本。利用这个方法,有很大比例的对抗样本可以带着目标标签迁移。我们还展示了一些几何学研究来帮助理解可迁移对抗样本。最后,我们展示了基于集成的方法能成功进行黑盒攻击。
1 简介
这章就是介绍了一下什么是对抗样本,现在大家研究的怎么样,哪些没人研究过,然后这篇文章就研究了这些。然后前半部分长篇大论的就没翻,只列了最后总结性的部分
Contributions and organization:
Section2:背景知识及实验设置
Section3:阐述了现有的能生成无目标可迁移对抗样本的方法
Section4:几乎没有现有的方法能够生成可迁移的有目标对抗样本
Section5:提出了一种新颖的基于集合的方法生成对抗样本,是首个能使大部分有目标对抗样本能够在多个模型间迁移的方法。
Section6:首个对ImageNet上训练出的大型模型进行几何特性分析,揭示了一些有趣的发现,例如不同模型的梯度方向是相互正交的。
Section7:首个展示能够在黑盒环境下进行有目标迁移的对抗样本,该对抗样本是利用在ImageNet上训练出的模型制造出来的,并且更值得一提的是,目标模型是Clarifai.com,其标签集与ImageNet的大不相同。
相关工作:对抗样本的迁移性2013年在 Intriguing properties of neural networks.上由Szegedy等人首次提出,其研究了同一数据集上训练出来的不同模型的迁移性以及一个数据集的不相交子集上训练出的不同模型的迁移性。
后续2014年Goodfellow在Explaining and harnessing adversarial examples.上提出将传递性归因于对抗扰动于模型的权重向量高度平行,该假设是在MNIST和CIFAR-10上验证的,本文证实了该假设对于ImageNet上训练的模型无效。
2016年Papernot在a: Transferability in machine learning: from phenomena to black-box attacks using adversarial samples.和b: Practical black-box attacks against deep learning systems using adversarial examples.提出构建一个替代模型来进行黑盒攻击,为了训练该模型,他们开发了一个技术,就是综合一个训练集,并通过查询目标模型来给其进行标签标注。后续,他们研究了深度神经网络与其他决策树、knn等模型间的迁移性。
我们的工作在三方面与Papernot等人不同:第一,在他们的研究中,只有模型和训练过程是黑盒的,训练集和测试集是攻击者掌握的,而本文攻击的模型,训练集,训练过程,测试集都是未知的。第二:这些研究都是基于MNIST和GTSRB等小规模数据集,而本文研究的是大模型及ImageNet等大数据集。第三:我们不通过查询目标系统来构建替代模型。
Moosavi-Dezfooli等人有一个同行且独立的研究,展示了一种能够在各个模型间迁移的“普适性扰动”,利用这种扰动生成的对抗图片可以在ImageNet上的各种模型间迁移。但他们只研究了无目标迁移性,然而我们的工作同时研究了ImageNet上的无目标和有目标攻击。
2 对抗深度学习及迁移性
2.1对抗深度学习问题
这一节就是定义了一下对抗样本问题
2.2:生成对抗样本的方法
本文考虑三类生成方法:基于优化的方法,快速梯度方法,及快速梯度符号方法。每类都分别有无目标和有目标版本。
其实我感觉就是分成了基于优化和基于梯度两类,梯度和梯度符号这两种方法就差了个sign函数。而基于优化的方法其实还是利用了梯度的,只不过是迭代的去利用梯度来生成对抗样本,而快速梯度符号方法(FGSM)只利用了一次梯度(所以叫快速嘛),所以本质上就是基于迭代和非迭代的方法,但是下面还是按作者的叫法,称为基于优化和基于梯度。
2.2.1无目标方法
一切无目标攻击都可形式化为寻找满足以下条件的x*:
基于优化的方法:近似出以下优化问题的最优解(具体见C&W方法):
快速梯度符号方法(FGSM):仅计算一次梯度,故称为“快速”(对应迭代方法,需多次计算梯度)。利用sign函数,生成的对抗图像满足∞范数约束。形式化:
其中,clip为裁剪函数,保证生成的图片各像素还在[0-255]范围内,sign为符号函数。
快速梯度方法(FG):类似FGSM,但不沿梯度符号方向,而是直接沿着梯度方向。
这一节主要就是介绍了一下三种方法,不了解的话可以直接看一下原文或者相关博客。
2.2.2有目标方法
类似于无目标攻击,但第一个约束条件改为:![]()
这一段感觉也没什么好说的,就是描述了一下有目标版本的三种方法。
2.3评估方法
这一节详细叙述了所研究的模型、训练集及所用的度量方法,作者讲述的比较复杂,我这里挑了几个比较值得关注的列一下:
-
Models. 一共五个:RestNet-50,ResNet-101, ResNet-152,GoogLeNet and VGG-16。
-
Dataset. 从ILSVRC2012验证集中选择100张能够被5个模型正确分类的图片作为测试集。
-
Measuring transferability. 这个很绕!划重点!!看仔细了,不然看后面的图表看不懂。这部分就是说怎么衡量一个对抗方法的好坏,分两种情况,一个是有目标,一个是无目标。对于无目标攻击,计算目标模型能够将对抗样本正确分类的概率;对于有目标攻击,计算目标模型错误分类,且输出结果为攻击者选定的目标标签的概率。所以说后面实验的表格中,如果是无目标攻击,则百分比越小说明攻击效果越好,而有目标攻击则是百分比越大说明效果越好。
3.无目标对抗样本
本章研究了各种生成无目标对抗图片的方法。
3.1 基于优化的方法
采用Adam优化器来优化上一章提到的优化问题。作者发现,可以通过调整Adam的学习率来调节均方根差(也就是图像扰动的大小),只要将学习率设置的很小,就能使对抗样本的均方根差很小,无论λ取何值。因此作者干脆将λ设为0。然后发现这些对抗样本虽然扰动很小,也能成功欺骗目标模型,但迁移性很差。
增加学习率,即增加扰动大小后,损失值在100次迭代后开始收敛。这样的对抗样本几乎都能百分百欺骗目标模型,且大部分可迁移。值得注意的使,虽然不同的ResNet模型结构相似,只有超参数不同,但他们生成的对抗样本不一定能相互迁移,但总体上比迁移到非RestNet模型上要容易。
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第1张图片](http://img.e-com-net.com/image/info8/d67505ef71b54a7d9992c497f84dfec8.jpg)
这个是实验结果,Panel A是优化方法的,Panel B是下面的快速梯度方法的,都是单模型无目标的,作者给出了以下几个结论:
- 对角线都是0,说明用某一模型生成的对抗样本可以百分百迁移到同类(比如都是ResNet-152)的黑盒模型上
- 大部分基于优化生成的无目标对抗样本都可以迁移到别的(非同类)模型上去。
- 虽然三个ResNet模型只有超参数不一样,但是它们三个之间的迁移不见得比迁移到别的模型上容易,比如第一列的3、4两格,RestNet-50迁移到RestNet-152准确率有23%,而VGG16迁移上去只有22%。
3.2快速梯度方法
这部分没仔细看。。。。。感觉没什么意思,不是本文的重点
3.3 加入随机扰动进行比较
就是对原图像加入随机的高斯噪声,然后测试模型的准确率,然后测试结果就是果然没有上面两个方法好。这个感觉过分了啊,这不是废话吗,,,感觉看不起这两个方法。
4.有目标攻击
这部分也没仔细看,也不是重点,结果总归就是有目标攻击成功率比无目标低。后面的集合攻击和几何分析才是全文的重点。![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第2张图片](http://img.e-com-net.com/image/info8/6f65350e65d54eb29a734fefb2293c39.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第3张图片](http://img.e-com-net.com/image/info8/350df5f720cc4ad58ce0be1af21d8465.jpg)
这是实验结果,注意,有目标攻击的实验结果百分百越大说明实验效果越好,这个和无目标的是相反的,具体原因看上面2.3里面Measuring transferability. 里说的。
5.基于集合的方法
作者提出了这样一个假设:如果一个对抗图片能够对多个模型保持对抗性,则他也更有可能能够迁移到别的模型上。因此,他提出了一个利用多个模型生成对抗样本的技术。
基本思路:就是利用一个模型集合来生成对抗图片。
形式化问题:给定k个白盒模型及其softmax输出J1,J2,…Jk,原始图片x及其真实标签y,y*为目标标签,则基于集合方法即为解决如下优化问题:
注:这里的优化问题是直接套用的C&W论文里面的结论,也就是把L(u,v)=log(1-u·v)直接带入到2.2.1的那个优化问题里,然后因为上述的是有目标攻击,所以就变成了log(u·v)。
然后作者将3、4章介绍的单个模型的攻击方法与本章所述的基于集合的方法相结合,形成了利用集合模型的攻击方法。
以下是对集合模型版的优化方法与梯度方法的评估:
Optimization-based approach. 利用Adam,计算四个模型的更新值并求和,然后加到图片上。同样在100次迭代后收敛了。制作出来的对抗样本普遍具有迁移性,不过并不能百分百欺骗集合中的模型。作者的解释是:在搜索集合模型的对抗样本的时候,并不会直接去误导集合中的某个单个的模型的预测值。
上述的是有目标攻击的结构,迁移后成功误导的几率大概百分之三四十(具体看表),而无目标部分效果就更好了,迁移后模型的准确率低于6%,且扰动大小也比单个模型的攻击要小。
下面是实验结果,第一个是有目标,数据越大说明效果越好,第二个是无目标的,数据越小说明效果越好。
Fast gradient-based approach. 作用不大,无目标部分,目标模型的正确率能达到20%,而有目标部分就更惨了,目标模型分到目标标签的成功率就1%。至于原因,作者的猜想是集合中的不同模型的梯度方向是相互正交的,这样一来集合模型的梯度方向就几乎和其中的单个模型的梯度方向正交了,因此就需要特别大的扰动才能有对抗性,具体分析在第六章。
下面是实验结果,第一个是无目标,第二个是有目标。
总结一下,就是作者提出将多个模型的softmax层的输出进行加权求和,然后将这个和看成是这几个模型组成的集合模型的softmax输出,然后再按传统的攻击方法来攻击。然后实验结果就是,对基于优化的方法提升很明显,而对基于梯度的方法几乎没什么提升。
接下来就是作者对于迁移性的一个深入分析,我感觉是这篇文章最重要的部分。
6.不同模型的几何特性
本章展示了模型的一些几何特性来试图更好的理解可迁移对抗样本。前人也做过相关工作,本文测试在大数据集上训练的,有1000个标签的大型模型,其几何特性并未被测试过。
结论一:在我们的评估中,不同模型的梯度方向几乎是相互正交的。 作者想研究不同模型的对抗方向是否相互一致。他计算了不同模型的梯度方向间夹角的余弦值(通过余弦值就可以反应夹角了嘛),发现任何两个模型的夹角的余弦值都接近于0,这表明对于大多数图像来说,他们关于不同模型的梯度方向是相互正交的。
这一段话是啥意思呢,说白了,从直觉上说,既然有迁移攻击这个东西,那不同模型的梯度方向应该是差不多的,这样你攻击了一个模型,这个对抗样本也就能攻击别的模型了嘛。作者就是想证实一下,结果发现不仅不是差不多,还几乎是垂直的(高维上叫正交)。这就很奇怪了,既然两个模型的梯度方向几乎是正交的,那你沿这个模型的梯度方向加扰动,拿去给别的模型用,按理说应该是百分百没用呀。然后作者就在后面做了进一步的研究。
结论二:单个模型的无目标方法的决策边界。作者希望通过研究不同模型的决策边界来理解为什么对抗样本能迁移。他选择了两个正交方向σ1σ2,一个是VGG16的梯度方向,另一个是随机选择的。每个点(u,v)对应了图片x+uσ1+vσ2,其中x是原始图片的像素值向量。对于每个模型,我们绘制每个点对应图片的标签,并利用图2的图片获得了图3。
作者这是要干啥呢,我的理解是:因为上面结论一说了,按照直觉不同模型的梯度应该是差不多的,这样才会出现迁移这个东西,但是作者一实验发现是两两正交的。这就奇了怪了,那为什么对抗样本还能迁移呢?所以作者就想搞明白这个,所以就先给图片加沿着梯度方向的扰动,从小到大开始加,看看什么时候模型开始出现错误,也就是碰到所谓的决策边界嘛。然后再给图片加正交于梯度方向的扰动,从小到大开始加,看看是什么情况,会不会出现误判,啥时候会出现。想到这儿,作者干脆就不光做这两个方向的实验,他把这两个方向进行线性组合,也就是文中说的u,v,然后u和v都取-20到20的所有值,测试一下模型的输出标签,然后不同的标签用不同的颜色表示,就形成了文章里的Figure3.
再后面是作者对这张图的观察和分析,我做一下提炼和总结(顺便提一下,Figure3上下两部分,一个Zoom-in一个Zoom-out只是放大缩小而已,是同一个东西):
- 1.每个模型都只有中间一小块可以保证正确分类(也就是所谓的决策边界嘛)
- 2.一个很有趣的现象:三个RestNet模型在沿着梯度方向,也就是沿x轴往左往右,第一个错误分类的类别是一样的,都是变成了亮绿色,其实就是都错误分类为了“橘子”。不过随着扰动进一步增大,错误分类的类别就五花八门了。
- 3.作者还统计了每个模型所出现的所有误判的类别,也就是随着扰动增大,各个模型一共对抗样本一共出现了几种错误结果,然后统计在了Table5.结果发现所有的模型加起来一共才出现了21种,但这个数据集一共有1000个类别,只有2.1%。这就解释了为什么梯度方法难以进行有目标攻击,因为你不管沿着梯度方向还是沿着正交方向,它一共只会出现这21种结果,你如果目标定成另外几百个标签中的一个,根本就不可能制造出这样的对抗样本。
- 4.每个模型的决策边界都差不多,这就是为什么无目标攻击是很好迁移的。
- 5.沿梯度方向的直径比沿随机的正交方向的直径要小,这个也很容易理解,因为沿梯度方向也就是扰动更有针对性嘛,模型自然更容易误判。
- 6.又一个很有趣且很反直觉的发现:沿着x轴向右,就是沿着梯度方向加入扰动,出现了误判,这很好理解,就是增大了正确标签的损失值嘛。但是向左移动,是在减小损失,相当于增加正确标签的概率,但是模型还是出现了误判。这就很奇怪了,作者的解释是这是由于损失函数的非线性导致的,扰动增大后,梯度方向也在剧烈变化,原本的梯度方向可能也就不再是减小损失的方向了。
- 7.这个点也挺有意思的,就是仔细看VGG-16的zoom-in的那张图,蓝色区域里面有一个橙色的小区域,蓝色区域就是模型分类正确的情况,橙色就是分类成别的东西了。作者用这个点来解释小扰动的无目标攻击不能百分百迁移,说是因为对于VGG来说,这个小区域内的扰动很小,也能导致VGG出错,但是他是VGG里面的一个特例,拿去攻击别的模型就不行,所以小扰动的无目标攻击不能百分百迁移。不过感觉这个解释也没啥必要,因为VGG16的决策边界本来就参差不齐的,随便哪里凹进来的一块,拿来攻击别的模型,也会导致迁移失败的。
结论三:有目标集合方法的决策边界。 然后作者又取了有目标攻击的集合模型的梯度方向及其垂直方向,然后和上面一样线性组合加在原图上,从而画出各个模型的决策边界。作者把五个模型的决策边界画在一张图里,也就是Figure5,然后这张图里面虚线画的四个模型就是集合模型的集合里面的四个模型,然后实线画出来的VGG不在集合里面。然后可以很明显的看出来集合里有的模型,攻击范围相对大一点,集合里没有的就要小很多。但是无论如何,他们的中心点还是差不多重合的。
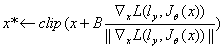
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第4张图片](http://img.e-com-net.com/image/info8/3b36f6080d334eb0aacb3ca2211e3f5f.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第5张图片](http://img.e-com-net.com/image/info8/0aecb5aee24d4009abf2d1a93c606558.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第6张图片](http://img.e-com-net.com/image/info8/cb733ee0c8384b14836dd28675d662cb.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第7张图片](http://img.e-com-net.com/image/info8/6aad1ec03d87424d91c6d5a0c71a2ccb.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第8张图片](http://img.e-com-net.com/image/info8/dfe43a4394254c79be680145a4366970.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第9张图片](http://img.e-com-net.com/image/info8/73f9f149f3444842a1fb75c72b3d780d.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第10张图片](http://img.e-com-net.com/image/info8/5371948dfc7a49d4b97e8185a412b2c6.jpg)
![[论文笔记]Delving into Transferable Adversarial Examples and Black-box Attacks(ICLR2017)_第11张图片](http://img.e-com-net.com/image/info8/af12f1bd52d044deb6b54b84c3e9c888.jpg)