基于MATLAB的关节型六轴机械臂轨迹规划仿真（2021实测完整代码）

基于MATLAB的关节型六轴机械臂轨迹规划仿真

1 实验目的

基于机器人学理论知识，利用标准D-H参数法建立关节型机器人的数学模型，使用Matlab的Robotics Toolbox工具包搭建模型。

tip：实验工具:Matlab R2021a （有很多玄学问题是因为软件版本）
以及注意先安装Robotics Toolbox工具包！！

2 实验内容

2.1标准D-H参数法

标准D-H参数法常用于建立关节型机器人的数学模型，D-H参数法是一种对连杆的坐标描述，而关节机器人本质上就是一系列连杆通过关节连接起来而组成的空间开式运动链。

对于连杆本身，其功能在于保持其两端的关节轴线具有固定的几何关系，连杆的特性由轴线决定，通常用四个连杆参数来描述，连杆长度，连杆扭转角，连杆偏移量和关节角。

本实验给定的参数表：

序号	Theta: 关节转角	D:关节距离	A:连杆长度	Alpha:连杆扭角	Offset:偏移
1	0	0.4	0.25	pi/2	0
2	pi/2	0	0.56	0	0
3	0	0	0.035	pi/2	0
4	0	0.515	0	pi/2	0
5	pi	0	0	pi/2	0
6	0	0.08	0	0	0

2.2实验中使用的Matlab函数

Link函数
用于定义六轴机器人的一个轴。
包含了机器人的运动学参数、动力学参数、刚体惯性矩参数、电机和传动参数；
可采用DH法建立模型,其中包含参数：关节转角，关节距离，连杆长度，连杆转角，关节类型（0转动，1移动）。

% 定义六轴机器人的一个轴
L(1) = Link([theta1, D1, A1, alpha1, offset1], 'standard')

SerialLink函数
用于构建机械臂。
它的类函数比较多，包括显示机器人、动力学、逆动力学、雅可比等；

% 'six'为机械臂名称
robot = SerialLink(L,'name','six');

fkine正解函数
用于求解出末端位姿p。

theta = [0.1,0,0,0,0,0];    %指定的关节角
p=robot.fkine(theta)        %fkine正解函数，根据关节角theta，求解出末端位姿p

ikine逆解函数
用于求解出关节角q。

q=ikine(robot,p)           %ikine逆解函数，根据末端位姿p，求解出关节角q

轨迹规划
（1）jtraj
已知初始和终止的关节角度，利用五次多项式来规划轨迹；

T1=transl(0.5,0,0);		  %根据给定起始点，得到起始点位姿
T2=transl(0,0.5,0);		  %根据给定终止点，得到终止点位姿
init_ang=robot2.ikine(T1);%根据起始点位姿，得到起始点关节角
targ_ang=robot2.ikine(T2);%根据终止点位姿，得到终止点关节角
step = 20;
[q ,qd, qdd]=jtraj(init_ang,targ_ang,step); %五次多项式轨迹，得到关节角度，角速度，角加速度，50为采样点个数

（2）ctraj
已知初始和终止的末端关节位姿，利用匀加速、匀减速运动来规划轨迹。

T0 = robot2.fkine(init_ang);%运动学正解
T1 = robot2.fkine(targ_ang);%运动学正解
Tc = ctraj(T0,T1,step);     %得到每一步的T阵
tt = transl(Tc);

3实验结果

4 全部代码

%% MATLAB素质三连
clear;
close all;
clc;
%% 实验一 基于MATLAB的关节型六轴机械臂仿真

%% 参数定义
%机械臂为六自由度机械臂
clear L;
 
%角度转换
angle=pi/180;  %度
 
%D-H参数表
theta1 = 0;   D1 = 0.4;   A1 = 0.025; alpha1 = pi/2; offset1 = 0;
theta2 = pi/2;D2 = 0;     A2 = 0.56;  alpha2 = 0;    offset2 = 0;
theta3 = 0;   D3 = 0;     A3 = 0.035; alpha3 = pi/2; offset3 = 0;
theta4 = 0;   D4 = 0.515; A4 = 0;     alpha4 = pi/2; offset4 = 0;
theta5 = pi;  D5 = 0;     A5 = 0;     alpha5 = pi/2; offset5 = 0;
theta6 = 0;   D6 = 0.08;  A6 = 0;     alpha6 = 0;    offset6 = 0;

%% DH法建立模型,关节转角，关节距离，连杆长度，连杆转角，关节类型（0转动，1移动）

L(1) = Link([theta1, D1, A1, alpha1, offset1], 'standard')
L(2) = Link([theta2, D2, A2, alpha2, offset2], 'standard')
L(3) = Link([theta3, D3, A3, alpha3, offset3], 'standard')
L(4) = Link([theta4, D4, A4, alpha4, offset4], 'standard')
L(5) = Link([theta5, D5, A5, alpha5, offset5], 'standard')
L(6) = Link([theta6, D6, A6, alpha6, offset6], 'standard')

% 定义关节范围
L(1).qlim =[-180*angle, 180*angle];
L(2).qlim =[-180*angle, 180*angle];
L(3).qlim =[-180*angle, 180*angle];
L(4).qlim =[-180*angle, 180*angle];
L(5).qlim =[-180*angle, 180*angle];
L(6).qlim =[-180*angle, 180*angle];

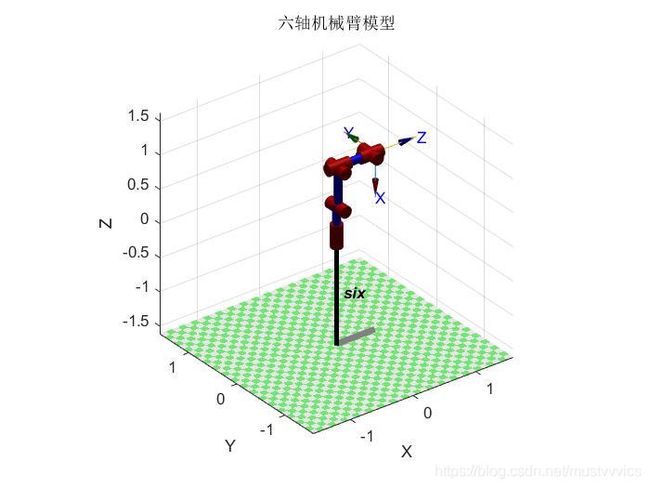
%% 显示机械臂
robot0 = SerialLink(L,'name','six');
f = 1 									%画在第1张图上
theta = [0 pi/2 0 0 pi 0];				%初始关节角度
figure(f)
robot0.plot(theta);
title('六轴机械臂模型');
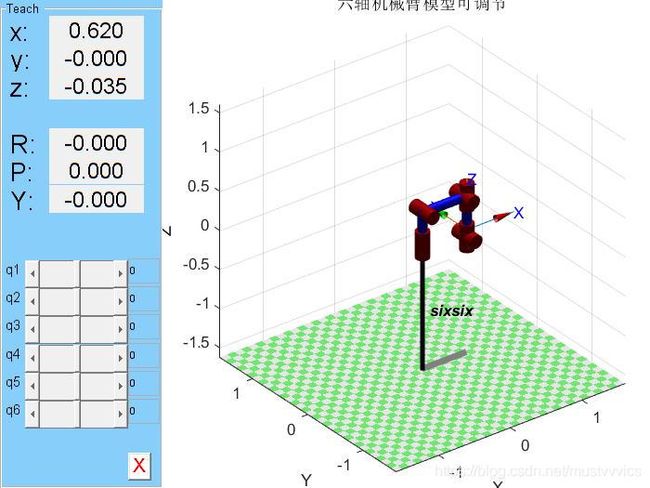
%% 加入teach指令，则可调整各个关节角度
robot1 = SerialLink(L,'name','sixsix');
f = 2
figure(f)
robot1.plot(theta);
robot1.teach
title('六轴机械臂模型可调节');
%% 实验二 基于MATLAB的六轴机械臂轨迹规划仿真

%% 2.2求解运动学正解
robot2 = SerialLink(L,'name','sixsixsix');
theta2 = [0.1,0,0,0,0,0];   			%实验二指定的关节角
p=robot2.fkine(theta2)       			%fkine正解函数，根据关节角theta，求解出末端位姿p
q=ikine(robot2,p)            			%ikine逆解函数，根据末端位姿p，求解出关节角q

%% 2.3 jtraj 已知初始和终止的关节角度，利用五次多项式来规划轨迹
% T1=transl(0.5,0,0);					%根据给定起始点，得到起始点位姿
% T2=transl(0,0.5,0);					%根据给定终止点，得到终止点位姿
T1=transl(0.5,0,0);						%根据给定起始点，得到起始点位姿
T2=transl(0,0.5,0);						%根据给定终止点，得到终止点位姿
init_ang=robot2.ikine(T1);				%根据起始点位姿，得到起始点关节角
targ_ang=robot2.ikine(T2);				%根据终止点位姿，得到终止点关节角
step = 20;
f = 3

%轨迹规划方法
figure(f)
[q ,qd, qdd]=jtraj(init_ang,targ_ang,step); %五次多项式轨迹，得到关节角度，角速度，角加速度，50为采样点个数
grid on
T=robot2.fkine(q);						%根据插值，得到末端执行器位姿
nT=T.T;
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹
title('输出末端轨迹');
robot2.plot(q);							%动画演示 

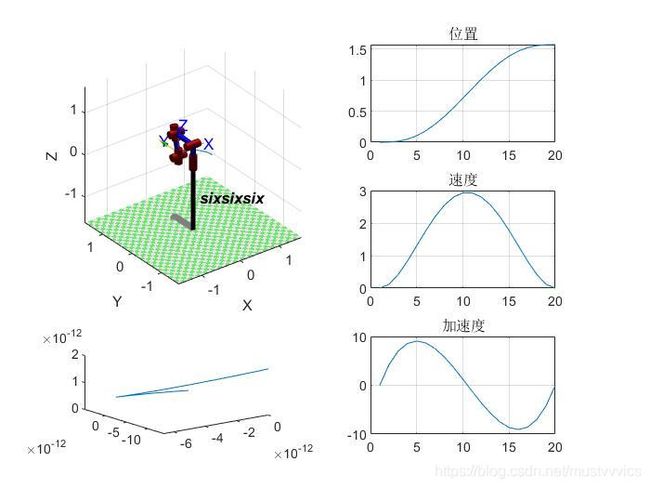
%% 求解位置、速度、加速度变化曲线
f = 4
figure(f)
subplot(3,2,[1,3]); 					%subplot 对画面分区 三行两列 占用1到3的位置
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹
robot2.plot(q);							%动画演示

figure(f)
subplot(3, 2, 2);
i = 1:6;
plot(q(:,1));
title('位置');
grid on;

figure(f)
subplot(3, 2, 4);
i = 1:6;
plot(qd(:,1));
title('速度');
grid on;

figure(f)
subplot(3, 2, 6);
i = 1:6;
plot(qdd(:,1));
title('加速度');
grid on;

t = robot2.fkine(q);					%运动学正解
rpy=tr2rpy(t);   						%t中提取位置（xyz）
figure(f)
subplot(3,2,5);
plot2(rpy);

%% ctraj规划轨迹 考虑末端执行器在两个笛卡尔位姿之间移动  
f = 5
T0 = robot2.fkine(init_ang);			%运动学正解
T1 = robot2.fkine(targ_ang);			%运动学正解

Tc = ctraj(T0,T1,step);  				%得到每一步的T阵

tt = transl(Tc);
figure(f)
plot2(tt,'r');
title('直线轨迹');