我的论文串讲「一」
文章目录
-
- [Done]2022-arXiv-It’s DONE Direct ONE-shot learning without training optimization
-
- Abstract
- Introduction
- Related work
- Methodology
- Implementation and Dataset
- Results and Discussion
- [Phase]2021-SPIE-Deep neural networks to improve the dynamic range of Zernike phase-contrast wavefront sensing in high-contrast imaging systems
-
- Abstract
- Introduction
- Optical Model and Simulation
- Static and Dynamic Neural Network Technology
- Results
- [Light]2022-arXiv-EdgeViTs Competing Light weight CNNs on Mobile Devices with Vision Transformers
-
- 简介
- 架构
- Local-Global-Local bottleneck
-
- Local aggregation
- Global sparse attention
- Local propagation
- PyTorch 实现
- 结构变体
- ImageNeT 精度 SOTA
- 实时性与精度对比
- 目标检测任务
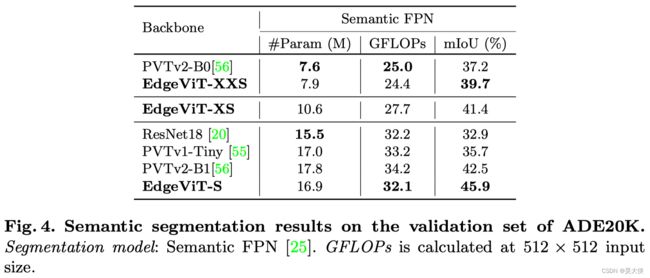
- 语义分割任务
[Done]2022-arXiv-It’s DONE Direct ONE-shot learning without training optimization
Abstract
本文受人脑可以在一个例子中学习一个概念的启发,提出了一种简单可行的一次性学习方法(依据 Hebbian 理论「如果一个神经元持续激活另一个神经元,前者的轴突将会生长出突触小体(如果已有,则会继续长大)和后者的胞体相连接」)
-
使用一个预训练的 DNN 网络
-
往分类器中添加一个新的类,即没有训练优化也没有对其他类修改,直接使用新附加类的数据输入模型后得到的最终密集层的权重作为新类的连接权,为新类提供一个输出神经元
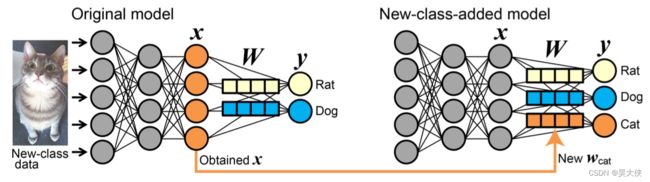
-
不需要调参性能完全取决于预训练模型
Introduction
一次性学习对于人类学习容易对于对于 DNN 很难,具体表现在人类可以从一个输入图像学习一个新的类别到自己的知识库,而 DNN 很难做到,除非特定的优化,但恰恰做到这一点在实际应用中非常有用。本文使用间接使用预训练模型的经验作为先验知识,在 Pretrained ImageNet 1000 classes 基于 VIT 或者 EffientNet(复合扩张的 CNN)添加一个或八个新类(机会水平小于 0.1 % 0.1\% 0.1%),准确率最多可达到 80 % 80\% 80%
- 受大脑启发,程序简单,首创
- 无优化,计算成本低
- 无超参数容易重现
Related work
度量学习、数据增强和元学习,Done 与他们都不同并不包含优化算法,性能由 Backbone 唯一决定,有助于理解大脑和 DNN 并提供一个 Baseline 方法
- 度量学习是为了减少属于一类的训练数据之间在度量空间的距离,如 Siamese 网络
- 数据增强增加训练数据的数量,如使用半监督的方法或者生成对抗的方法
- 元学习 提高学习效率,从少量训练数据中学习(从出发点上来看元学习有点类似 model pretraining 都是让网络具有一些先验知识)
Methodology
分类任务中输出向量 y y y 表示输入数据属于每个类的程度
y i = x ⋅ w i + b i = ∥ x ∥ ∥ w i ∥ c o s θ + b i , i ∈ c l a s s { 1 , ⋯ , N } y_i = x\cdot w_i + b_i=\parallel x\parallel\parallel w_i\parallel cos\theta + b_i,i\in class\{1,\cdots,N\} yi=x⋅wi+bi=∥x∥∥wi∥cosθ+bi,i∈class{1,⋯,N}
“Done directly apply x x x obtained from a new-class input image to the weight vector for the new class w j ( j = N + 1 , ⋅ ⋅ ⋅ ) w_j (j = N + 1, · · ·) wj(j=N+1,⋅⋅⋅). To convert x x x to w j w_j wj, we apply quantile normalization, statistical properties of the elements of new vector w j w_j wj are the same as those of the elements of original W W W matrix. As for b j b_j bj, we employed the median of b b b.”
y j = x ⋅ w j + b j = ∥ x ∥ ∥ w j ∥ c o s θ + b j , j ∈ c l a s s { 1 , ⋯ , N + 1 , ⋯ } y_j = x\cdot w_j + b_j=\parallel x\parallel\parallel w_j\parallel cos\theta + b_j,j\in class\{1,\cdots,N+1,\cdots\} yj=x⋅wj+bj=∥x∥∥wj∥cosθ+bj,j∈class{1,⋯,N+1,⋯}
-
quantile normalization 即分位数归一化,生物信息学中的标准技术,因为 x x x(神经活动)与 W W W(突触强度)的统计特性可能是不同的,例如令 w j w_j wj 的均值与方差与 W W W 相同

但是不清楚是否需要三阶矩,因此最简单的方法就是不分开来讨论而是使 w j w_j wj 和 W W W 的每一个元素的统计性质(均值)都相同。在 x x x 向 w j w_j wj 转换时,分位数归一化利用 x x x 的秩信息与 W W W 的值信息,使 w j w_j wj 与 W W W 之间的所有分位数相等,即 w j w_j wj 向量各元素的统计性质与原始 W W W 矩阵的统计性质相同(概率分布相同)
Implementation and Dataset
“As backbone models for our method, we employed Vision Transformers for images (ViT) and EfficientNet as two representative DNNs with different characteristics. We used “vit-keras” for ViT and “EfficientNet Keras (and TensorFlow Keras)” for EfficientNet. Also, for demonstrating evaluation of DNNs in DONE, we used ResNet-50, MobileNetV2, and VGG16, using Tensorflow. All models used in this study are pretrained with ImageNet.
We used CIFAR-100 and CIFAR-10 for the additional class, using Tensorflow. Also, for demonstrating evaluation of DNNs in DONE, we used CIFAR-FS by Torchmeta. We used ImageNet images for testing the performance of models. We used a coarse 10 categorization of the original 1000 classes, using information of previous 67 categorization. All images were resized to (224 × 224) by OpenCV or Tensorflow.”
Results and Discussion
“pretrained with ImageNet (1000 classes), As new additional classes, we chose eight classes, “baby”, “woman”, “man”, “caterpillar”, “cloud”, “forest”, “maple_tree”, and “sunflower” from CIFAR-100, which were not in ImageNet”
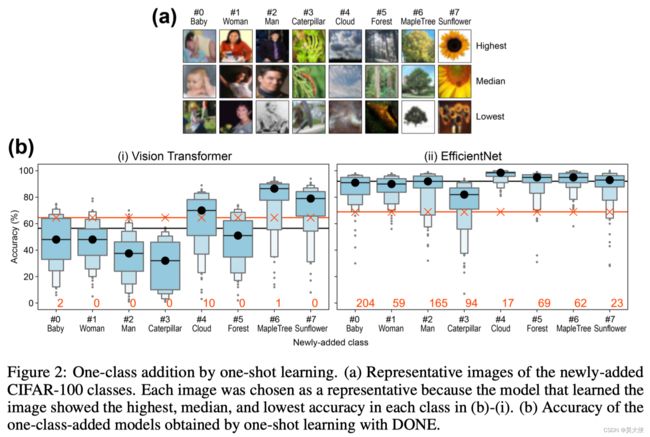
“Actually there is small interference, and Figure 2 ( b ) 2(b) 2(b) also shows the numbers of images in which the original model and added model gave different answers in the 50,000 images (orange numbers), regardless of whether it is correct or not. When we checked the all two ImageNet-validation images that was classified as “baby” by ViT, each of both images indeed contained a baby though its class in ImageNet was “Bathtub” (image ID: 00013344 and 00020254). Therefore, observed interference was not mistake but just the result of another classification. EfficientNet obviously shows greater numbers of interference (Figure 2 ( b ) 2(b) 2(b)), but we also confirmed that similar thing happened, e.g., 198 of the 204 ImageNet-validation images classified as “baby” in EfficientNet contained human or doll.”
在一次学习中,一次训练的不佳图像会导致糟糕的表现,反之亦然。在这个评价中,一些模型由于训练图像不好而表现出较低的性能,例如在 ViT 中,当训练图像是如图 2 ( a ) 2(a) 2(a) 左下角所示的婴儿图像时,准确率为 6 % 6\% 6%。因此在一次性学习的实际应用中,应该使用具有代表性的图像进行训练
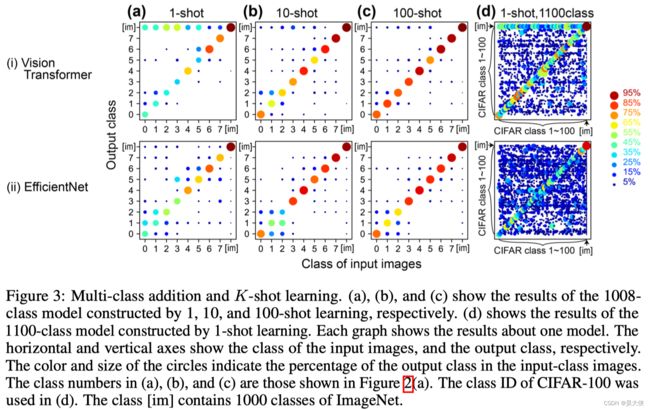
增加训练图像的数量作为 K-shot 学习。在 10 次学习的情况下图 3 ( b ) 3(b) 3(b),输入每一幅图像得到每一个 x x x,并将这 10 10 10 个 x x x 向量的均值向量转换为 w j w_j wj。使用了在 CIFAR-100 中的索引为每类从前到后的 10 10 10 张图像。用同样的方法测试了 100 100 100 次学习图 3 ( c ) 3(c) 3(c)。结果发现这种简单的平均操作稳步提高了精度 8 8 8 类的平均精度为 77.5 % 77.5\% 77.5% 和 74.5 % 74.5\% 74.5% 的 10 10 10 次和 86.1 % 86.1\% 86.1% 和 82.1 % 82.1\% 82.1% 的 100 100 100 次
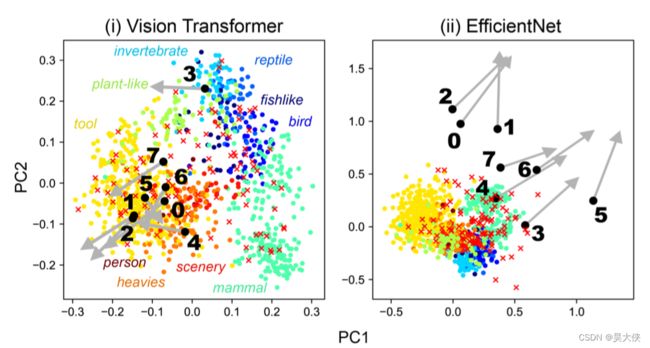
图 3 ( a ) 3(a) 3(a) 所示的一次性学习构建的 1008 1008 1008 类模型中每个 w i w_i wi 和 w j w_j wj 向量的 主成分分析。彩色的圆圈显示了 w i w_i wi 在原始 1000 1000 1000 个类中的结果。不同的颜色显示了类的粗略分类。黑色圆圈表示 w j w_j wj 的结果。随附的编号是图 2 ( a ) 2(a) 2(a) 中所示的新添加的类编号。图 3 ( c ) 3(c) 3(c) 所示的 100 次学习构建的模型中, w j w_j wj 是从黑色圆圈开始的灰色箭头的结果。红色的叉表示另一种情况,即 w j w_j wj 向量是 ImageNet 验证图像前 100 100 100 个验证 ID 的结果,EfficientNet 添加的新类特征更分散,因此可以印证效果更好
[Phase]2021-SPIE-Deep neural networks to improve the dynamic range of Zernike phase-contrast wavefront sensing in high-contrast imaging systems
Abstract
为了在高对比度成像中保持高对比度暗区,仪器中的光学像差必须最小化。本文研究了基于相位对比度的泽尼克波前传感器(ZWFS)用于大口径拼接口径望远镜的像差测量和校正。ZWFS 实现了亚纳米波前的精确传感,但其响应是非线性的。最近,利用深度神经网络(DNNs)从强度测量中实现相位检索已在几种光学系统中得到证实。在基于 Lyot 的低阶波前传感器(LLOWFS)线性系统中,使用 DNNs 而不是线性回归已被证明可以极大地扩展传感器的可用动态范围。在这项工作中,我们研究了使用两种不同类型的机器学习算法来扩展 ZWFS 的动态范围。利用模拟的 ZWFS 强度测量,我们验证了网络训练技术和目前的相位重建结果,ZWFS 传感器的捕获范围增加了 3.4 倍的单一波长和 4.5 倍的四波长
Introduction
AO 系统由一个或多个波前传感器(WFS)和一个驱动器组件(如变形镜(DM))组成。该系统用于一个闭环,其中来自WFS的相位测量用于将校正位移应用到DM。有许多不同的波前传感器技术,但泽尼克波前传感器(ZWFS)已被证明存在光子噪声下具有最佳的灵敏度
ZWFS 使用一个具有小区域相位不连续的焦平面相位对比度掩模,从而产生相移参考波。参考波与被测波相干扰重新成像的瞳孔中的波前,将相位误差转换为可以用传感器测量的强度变化,然而,当瞳孔中存在较大的未知波前误差时,分析方法就失效了。传感器响应保持单调的范围为 − 0.14 λ −0.14\lambda −0.14λ 到 0.36 λ 0.36\lambda 0.36λ。在波前均方根误差(RMS)较大的情况下,波前传感器像素之间存在显著的串扰。换句话说,重新成像的瞳孔中任何一个像素的强度并不仅仅依赖于瞳孔平面相应区域的波前位移
基于深度神经网络的静态和动态机器学习算法应用于 ZWFS 的反问题,动态机器学习算法是一种包含可训练细胞的递归的算法而静态神经网络不使用递归,使用模拟 ZWFS 数据评估这些技术
循环单元用于沿定义了某些动态的轴(通常是时间轴)接收多个输入,可以通过在多个波长收集 ZWFS 数据并实现网络沿波长轴的递归来提供的附加信息
Optical Model and Simulation
“The simulation is performed using the Physical Optics Propagation in Python (POPPY) library”
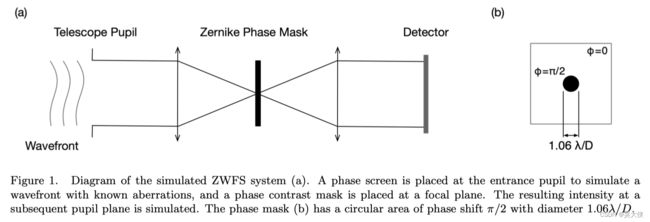
图 1 1 1 所示的光学系统由直径 6 6 6 米的圆形瞳孔和焦平面相位对比掩模组成,在系统的输入端提供一个具有选择光程差(OPD)误差图的波前,然后通过面具传播到重新成像的瞳孔,在那里产生的强度被记录下来,依靠 “Fast computation of lyot-style coronagraph propagation” 中描述的矩阵傅里叶变换(MFT)方法,在充分采样的情况下,通过焦平面掩模的小中心特征有效地进行传播。中心波长为 1.0 μ m 1.0\mu m 1.0μm 时,相位掩码 OPD 设为 π / 2 \pi/2 π/2,而输出强度模拟在 a t 0.96 μ m 、 0.98 μ m 、 1.0 μ m 、 1.2 μ m at\;0.96\mu m、0.98\mu m、1.0\mu m、1.2\mu m at0.96μm、0.98μm、1.0μm、1.2μm 4 4 4 个波长,用于网络训练

为了训练和测试神经网络,通过构造 c k c_k ck 的值来生成示例波阵面,使得得到的 E R M S E^{RMS} ERMS 值均匀分布在 0 ~ 500 n m 0~500 nm 0~500nm 之间。对于 8000 8000 8000 个训练数据、 1600 1600 1600 个验证数据和 3000 3000 3000 个测试数据中的每一个都进行了四个波长的模拟
Static and Dynamic Neural Network Technology
“The static neural network that we implement for this study is the Phase Extraction Neural Network(PhENN)a U-net structure in Figure(a). By varying the wavelength with four different values( λ 1 , ⋯ , λ 4 \lambda1,\cdots,\lambda4 λ1,⋯,λ4)we get four intensity patterns( g 1 , ⋯ , g 4 g_1,\cdots,g_4 g1,⋯,g4)each corresponding to a wavelength, which are deeply correlated with each other. The RNN is designed to exploit this correlation among the measurements by using a recurrent unit called Gated Recurrent Unit(GRU)in Figure2(b).”

图 ( a ) (a) (a) 是静态网络,独立的输入 g 1 , g 2 , g 3 , g 4 g_1,g_2,g_3,g_4 g1,g2,g3,g4 而图 ( b ) (b) (b) 把 g 1 , g 2 , g 3 , g 4 g_1,g_2,g_3,g_4 g1,g2,g3,g4 并行输入并且使用 G R U GRU GRU 相关联起来,将一个问题看作是一个前后关联具有链状结构的多阶段过程并定义为动态网络
Results
在图 3 3 3 中展示了来自测试数据集的单个示例波前的重构结果
在图 4 4 4 中利用了皮尔逊相关系数度量真实波前映射和估计波前映射之间的线性相关

每个实例的估计误差与初始 R M S RMS RMS 波前误差 E R M S E_{RMS} ERMS 之间的关系如图 5 5 5

[Light]2022-arXiv-EdgeViTs Competing Light weight CNNs on Mobile Devices with Vision Transformers
简介
在计算机视觉领域,基于 Self-attention 的模型(如 ViTs)已经成为 CNN 之外的一种极具竞争力的架构。尽管越来越强的变种具有越来越高的识别精度,但由于 Self-attention 的二次复杂度,现有的 ViT 在计算和模型大小方面都有较高的要求
虽然之前的 CNN 的一些成功的设计选择(例如,卷积和分层结构)已经被引入到最近的 ViT 中,但它们仍然不足以满足移动设备有限的计算资源需求。这促使人们最近尝试开发基于最先进的 MobileNet-v2 的轻型 MobileViT 但 MobileViT 与 MobileNet-v2 仍然存在性能差距
本文进一步推进这一研究方向,引入了 EdgeViTs,一个新的轻量级 ViTs 家族,也是首次使基于 Self-attention 的视觉模型在准确性和设备效率之间的权衡中达到最佳轻量级 CNN 的性能,通过引入一个基于 Self-attention 和卷积的最优集成的高成本的 local-global-local(LGL)信息交换瓶颈来实现的。对于移动设备专用的评估不依赖于不准确的 proxies 如 FLOPs 的数量或参数,而是采用了一种直接关注设备延迟和能源效率的实用方法如图 1 1 1
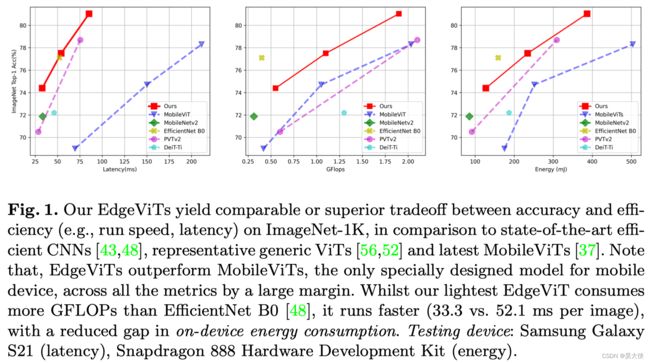
在图像分类、目标检测和语义分割方面的大量实验验证了 EdgeViTs 在移动硬件上的准确性-效率权衡方面与最先进的高效 CNN 和 ViTs 相比具有更高的性能。具体地说,EdgeViTs 在考虑精度-延迟和精度-能量权衡时是帕累托最优的,几乎在所有情况下都实现了对其他 ViT 的超越,并可以达到最高效CNN的性能
架构
本文采用了 ViT 变体中的分层金字塔结构的 Pyramid Transformer 模型,如图 2 ( a ) 2(a) 2(a),通过逐步聚集空间 Token(In CV Is Piexl,Other NLP Span Is Image)不同阶段在降低空间分辨率同时扩展通道维度。每个阶段由多个基于 Transformer Block 处理相同形状的张量,严重依赖于具有二次复杂度的 Self-attention 操作,其复杂度与视觉特征的空间分辨率呈 2 2 2 次关系

本文深入 Transformer Block 并引入了一个高效的 Bottlneck Local-Global-Local(LGL)实现了更好的准确性-延迟平衡,如图 2 ( b ) 2(b) 2(b) 其中使用一个稀疏注意力模块进一步减少了 Self-attention 的开销,如图 2 ( c ) 2(c) 2(c)
Local-Global-Local bottleneck
Self-attention 已被证明是非常有效的学习全局信息或长距离空间依赖性的方法,是视觉识别的关键。另一方面,由于图像具有高度的空间冗余(附近的 Patch 在语义上是相似的)将注意力集中到所有的空间 Patch 上,即使是在一个下采样的特征映射中,也是低效的,因此,与以前在每个空间位置执行 Self-attention 的 Transformer Block 相比 LGL Bottleneck 只对输入 Token 的子集计算 Self-attention 但支持完整的空间交互,如在标准的 Multi-Head Self-attention(MHSA)中。既会减少 Token 的作用域,同时也保留建模全局和局部上下文的底层信息流,为了实现这一点,作者将 Self-attention 分解为连续的模块,处理不同范围内的空间 Token 如图 2 ( b ) 2(b) 2(b)
引入了 3 3 3 种有效的操作
Local aggregation 仅集成来自局部近似 Token 信号的局部聚合
Global sparse attention 建模一组代表性 Token 之间的长期关系,其中每个 Token 都被视为一个局部窗口的代表
Local propagation 将代表学习到的全局上下文信息扩散到具有相同窗口的非代表 Token
结合起来 LGL Bottleneck 就能够以低计算成本在同一特征映射中的任何一对 Token 之间进行信息交换可以表达为
X = L o c a l A g g ( N o r m ( X i n ) ) + X i n Y = F F N ( N o r m ( X ) ) + X Z = L o c a l P r o p ( G l o b a l S p a r s e A t t n ( N o r m ( Y ) ) ) + Y X o u t = F F N ( N o r n ( Z ) ) + Z \begin{aligned} X &= LocalAgg(Norm(X_{in}))+X_{in}\\ Y &= FFN(Norm(X))+X\\ Z &= LocalProp(GlobalSparseAttn(Norm(Y)))+Y\\ X_{out} &= FFN(Norn(Z))+Z \end{aligned} XYZXout=LocalAgg(Norm(Xin))+Xin=FFN(Norm(X))+X=LocalProp(GlobalSparseAttn(Norm(Y)))+Y=FFN(Norn(Z))+Z
其中 X i n ∈ R H × W × C X_{in}\in R^{H\times W\times C} Xin∈RH×W×C 表示输入张量。Norm 是 Layer Normalization 操作,LocalAgg 表示局部聚合算子,FFN 是一个双层感知器,GlobalSparseAttn 是全局稀疏 Self-attention,LocalProp 是局部传播运算符(其中省略了位置编码)
本文质疑了像素级 Self-attention 的必要性,并探索由 LGL bottleneck 所支持的信息交换在多大程度上可以近似于标准的 MHSA,LGL bottleneck 同时使用分布在一系列局部-全局-局部操作中的 Self-attention 操作和卷积操作与最近的 PVTs 和 Twins-SVTs 模型有一个相似的目标即减少 Self-attention 开销
PVTs 执行 Self-attention 其中 Key 和 Value 的数量通过 strided-convolutions 减少,而 Query 的数量保持不变。换句话说,PVTs 仍然对每个像素位置执行 Self-attention
Twins-SVTs 结合了 Local-Window Self-attention 和 PVTs 的 Global Pooled Attention。这不同于 LGL bottleneck 的混合设计
Local aggregation
对于每个 Token 利用 Depth-wise 和 Point-wise 卷积在大小为 k × k k\times k k×k 的局部窗口中聚合信息图 3 ( a ) 3(a) 3(a)
Global sparse attention
对均匀分布在空间中的稀疏代表性 Token 集进行采样,每个 r × r r\times r r×r 窗口有一个代表性 Token 其中 r r r 表示子样本率。然后,只对这些被选择的 Token 应用 Self-attention 如图 3 ( b ) 3(b) 3(b) 与现有的 ViTs(所有的空间 Token 都作为 Self-attention 计算中的 query)不同
Local propagation
通过转置卷积将代表性 Token 中编码的全局上下文信息传播到它们的相邻的 Token 中图 3 ( c ) 3(c) 3(c)
PyTorch 实现
class LocalAgg():
def __init__(self, dim):
self.conv1 = Conv2d(dim, dim, 1)
self.conv2 = Conv2d(dim, dim, 3, padding=1, groups=dim)
self.conv3 = Conv2d(dim, dim, 1)
self.norm1 = BatchNorm2d(dim)
self.norm2 = BatchNorm2d(dim)
def forward(self, x):
"""
[B, C, H, W] = x.shape
"""
x = self.conv1(self.norm1(x))
x = self.conv2(x)
x = self.conv3(self.norm2(x))
return x
class GlobalSparseAttn():
def __init__(self, dim, sample_rate, scale):
self.scale = scale
self.qkv = Linear(dim, dim * 3)
self.sampler = AvgPool2d(1, stride=sample_rate)
kernel_size=sr_ratio
self.LocalProp = ConvTranspose2d(dim, dim, kernel_size, stride=sample_rate, groups=dim
)
self.norm = LayerNorm(dim)
self.proj = Linear(dim, dim)
def forward(self, x):
"""
[B, C, H, W] = x.shape
"""
x = self.sampler(x)
q, k, v = self.qkv(x)
attn = q @ k * self.scale
attn = attn.softmax(dim=-1)
x = attn @ v
x = self.LocalProp(x)
x = self.proj(self.norm(x))
return x
class DownSampleLayer():
def __init__(self, dim_in, dim_out, downsample_rate):
self.downsample = Conv2d(dim_in, dim_out, kernel_size=downsample_rate, stride=
downsample_rate)
self.norm = LayerNorm(dim_out)
def forward(self, x):
x = self.downsample(x)
x = self.norm(x)
return x
class PatchEmbed():
def __init__(self, dim):
self.embed = Conv2d(dim, dim, 3, padding=1, groups=dim)
def forward(self, x):
return x + self.embed(x)
class FFN():
def __init__(self, dim):
self.fc1 = nn.Linear(dim, dim*4)
self.fc2 = nn.Linear(dim*4, dim)
def forward(self, x):
x = self.fc1(x)
x = GELU(x)
x = self.fc2(x)
return x
结构变体
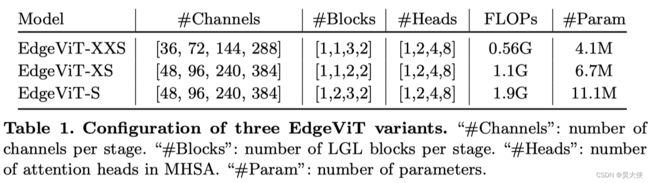
ImageNeT 精度 SOTA

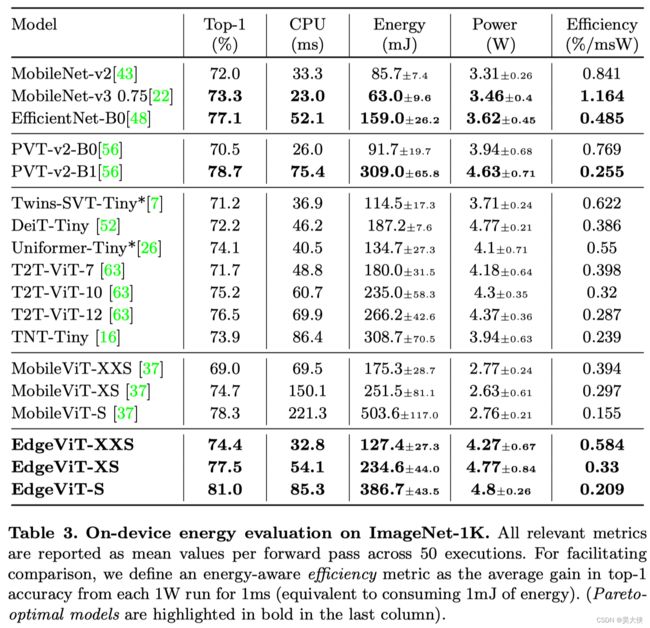
实时性与精度对比
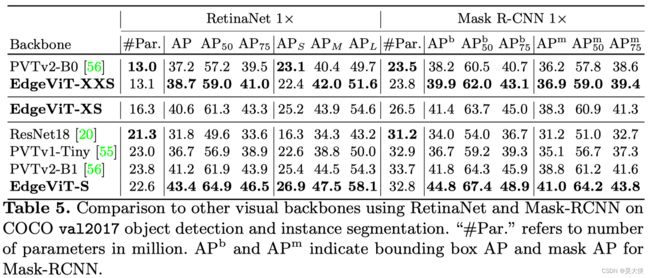
目标检测任务
语义分割任务