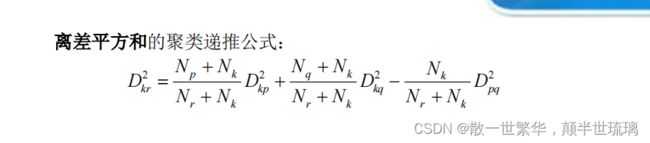统计分析:聚类分析(详细讲解)
聚类分析是研究“物以类聚”的一种方法。 人类认识世界往往首先将被认识的对象进行分类,早起人们主要靠经验和专业知识实现分类,但随着生产技术和社会科学的发展,对分类学的要求越来越高,靠经验和专业知识来分类越来越难,于是数学这一有力工具被引入分类学中,形成了数值分类学。后来随着多元分析的引进,聚类分析又逐渐从数值分类学中分离出来而形成一个相对独立的分支。
聚类分析法的一般步骤: 首先,不论是定量数据还是定性数据,都应确定分类统计量,用来测定样本之间的亲疏程度,主要通过样本之间的距离,样本间的相关系数来确定,其次,利用统计量将样本进行分类。
1.分类统计量
设有 N 个样品,每个样品测得 p项指标(变量),原始资料矩阵为
X = [ x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋮ x N 1 x N 2 ⋯ x N p ] X=\begin{bmatrix} x_{11} &x_{12} & \cdots & x_{1p}\\ x_{21} &x_{22} & \cdots & x_{2p}\\ \vdots & \vdots & &\vdots \\ x_{N1} &x_{N2} &\cdots &x_{Np} \end{bmatrix} X=⎣⎢⎢⎢⎡x11x21⋮xN1x12x22⋮xN2⋯⋯⋯x1px2p⋮xNp⎦⎥⎥⎥⎤
其中,矩阵的每一行代表一个样品,而每一列则代表样品的一项指标。
其中 x i j ( i = 1 , 2 ⋯ , N , j = 1 , 2 , ⋯ , p ) x_{ij}(i=1,2\cdots ,N,j=1,2,\cdots ,p ) xij(i=1,2⋯,N,j=1,2,⋯,p)为第 i i i个样品的第 j j j个指标的观测数据。第 i i i个样品 X i X_{i} Xi为矩阵 X X X的第 i i i行所描述,所以任何两个样品 X k X_{k} Xk与 X l X_{l} Xl之间相似性,可以通过矩阵 X X X中的第 k k k行与第 l l l行的相似程度来刻画;任何两个指标 x k x_{k} xk与 x l x_{l} xl之间的相似性,可以通过第 k k k与第 l l l列的相似程度来刻画。
对 N N N个样品进行分类的方法,称为Q型聚类法,常用的统计量用距离来表达;按 k k k个指标(或变量)进行分类的方法,称为R型聚类法,常用的统计量用相似系数来表达。距离和相似系数又通称为广义距离。
1.距离
如果把 N N N个样品( X X X中的 N N N行)看成 p p p维空间中的 N N N个点,那么两个样品间相似程度可用 p p p维空间中两点的距离来度量。令 d i j d_{ij} dij表示样品 X i X_{i} Xi与 X j X_{j} Xj的距离。
主要可分为明氏(Minkowski)距离,马氏距离以及兰氏距离。而明氏距离又可分为聚堆绝对距离,欧式距离(两点间距离公式)以及切比雪夫距离。
(1)明氏距离

(2)马氏距离


(3)兰氏距离

2.相似系数
通常所说的相关系数,是指变量(指标)间的相关系数,作为刻画样品间的相似关系也可给出类似定义,即第 i i i个样品与第 j j j个样品之间的相关系数可定义为:
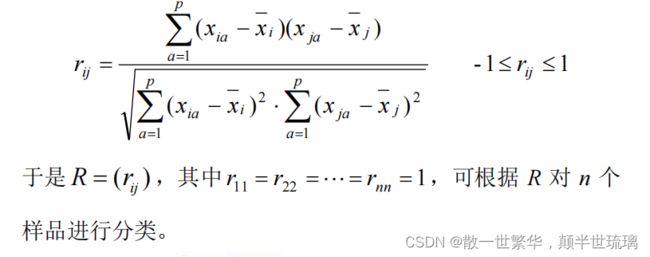
其中, x i ˉ = 1 p ∑ a = 1 p x i a \bar{x_{i}}=\frac{1}{p}\sum_{a=1}^{p}x_{ia} xiˉ=p1∑a=1pxia,即使矩阵 X X X第 i i i行的平均值,同理 x j ˉ = 1 p ∑ a = 1 p x j a \bar{x_{j}}=\frac{1}{p}\sum_{a=1}^{p}x_{ja} xjˉ=p1∑a=1pxja,即矩阵 x x x第 j j j行的平均值。
2.常用的聚类方法
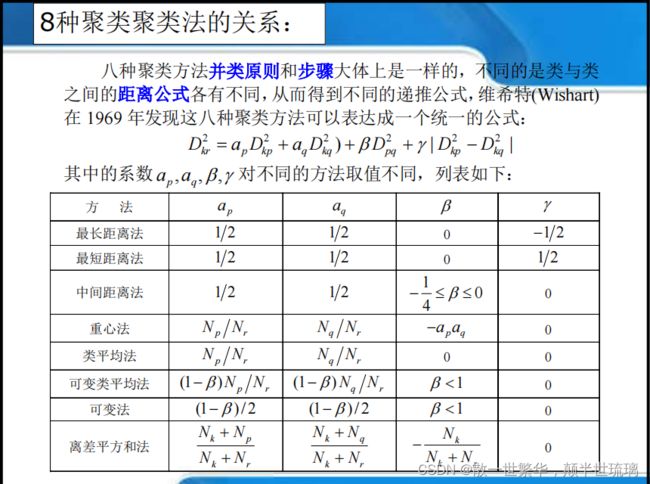
系统聚类分析法是目前国内外使用最多的一种方法,一般方法是:设有 N 个样品,初始时这 N 个样品各自成一类,然后计算样品之间的距离,将距离最小的类并为一新类,再计算并类后的新类与其它类的距离,又将距离最小的两类并为一新类,这样每次减少一些类,直到将 N 个样品合并成一类为止。正如样品之间距离可以有不同的定义方法一样,类与类之间的距离也有许多定义方法,下面给出常用的八种定义距离的方法,分别进行聚类,导出了八种聚类计算距离的递推公式,最后给出一种统一形式。这八种聚类方法是:最短距离法、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法、离差平方和法。
1.最短距离法
2.最长距离法
3.中间距离法
4.质心距离法(重心法)
5.类平均法
6.可变类平均法
类平均法虽然是一个较好的方法,但也有不足,递推公式中没有反映 D p q D_{pq} Dpq的影响,于是有人提出递推公式改为:
D k r 2 = N p N r ( 1 − β ) D k p 2 + N q N r ( 1 − β ) D k q 2 + β D p q 2 D_{kr}^{2}=\frac{N_{p}}{N_{r}}(1-\beta )D_{kp}^{2}+\frac{N_{q}}{N_{r}}(1-\beta )D_{kq}^{2}+\beta D_{pq}^{2} Dkr2=NrNp(1−β)Dkp2+NrNq(1−β)Dkq2+βDpq2
其中 β \beta β是可变的且 β < 1 \beta<1 β<1。
7.可变法
如果让中间距离法的距离公式中前两项系数也依赖于 β \beta β,即
D k r 2 = ( 1 − β ) 2 ( D k p 2 + D k q 2 ) + β D p q 2 − 1 4 ⩽ β ≤ 0 D_{kr}^{2}=\frac{(1-\beta)}{2}(D_{kp}^{2}+D_{kq}^{2})+\beta D_{pq}^{2} -\frac{1}{4}\leqslant \beta \leq 0 Dkr2=2(1−β)(Dkp2+Dkq2)+βDpq2−41⩽β≤0
利用上述公式进行聚类的方法叫可变法。
8.离差平方和法
3.用MATLAB进行聚类
1.MATLAB中有关聚类分析的命令
(1)pdist函数

(2)squareform函数

(3)linkage函数

(4)dendrogram函数

(5)cophenet函数

(6)cluster函数

2.应用举例

这里选取了发达国家,新兴工业化国家,拉美国家,亚洲发展中国家,转型国家不同类型的19个国家做Q型聚类分析。描述信息基础设施的变量主要有6个:
call表示每千个人拥有的电话线数;
movecall表示每千户居民蜂窝移动电话数;
fee表示高峰时期没三分钟国际电话的成本;
computer表示每千人拥有的电话数;
mips表示每千人中计算机功率;
net表示每千人互联网户主数。
3.编程求解
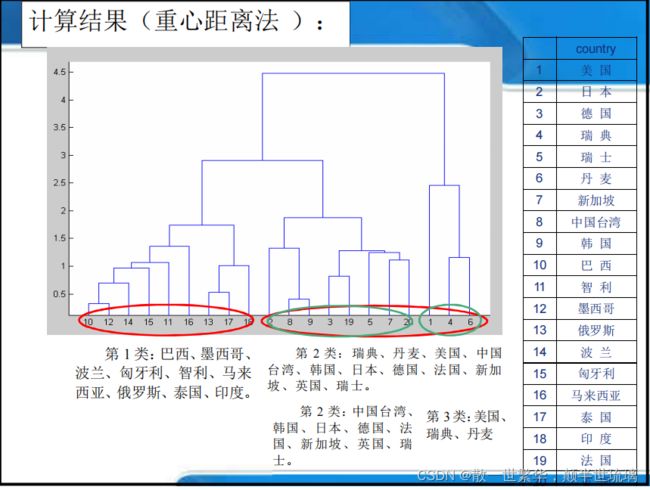
采用欧式距离和质心距离法进行分类,利用matlab编程:
x=[631.60 161.90 0.36 403.00 26073.00 35.34
498.40 143.20 3.57 176.00 10223.00 6.26
557.60 70.60 2.18 199.00 11571.00 9.48
684.10 281.80 1.40 286.00 16660.00 29.39
644.00 93.50 1.98 234.00 13621.00 22.68
620.30 248.60 2.56 296.00 17210.00 21.84
498.40 147.50 2.50 284.00 13578.00 13.49
469.40 56.10 3.68 119.00 6911.00 1.72
434.50 73.00 3.36 99.00 5795.00 1.68
81.90 16.30 3.02 19.00 876.00 0.52
138.60 8.20 1.40 31.00 1411.00 1.28
92.20 9.80 2.61 31.00 1751.00 0.35
174.90 5.00 5.12 24.00 1101.00 0.48
169.00 6.50 3.68 40.00 1796.00 1.45
262.20 49.40 2.66 68.00 3067.00 3.09
195.50 88.40 4.19 53.00 2734.00 1.25
78.60 27.80 4.95 22.00 1662.00 0.11
13.60 0.30 6.28 2.00 101.00 0.01
559.10 42.90 1.27 201.00 11702.00 4.76
521.10 122.50 0.98 248.00 14461.00 11.91];
x2=zscore(x); %数据标准化
y2=pdist(x2,‘euclidean’); %采用欧氏距离计算样品距离
z2=linkage(y2,'centroid') %采用重心距离法
c2=cophenet(z2,y2) %利用pdist函数生成的Y和linkage
函数生成的Z计算cophenet相关系数。
t=cluster(z2,6) %根据linkage函数的输出Z2创建分类
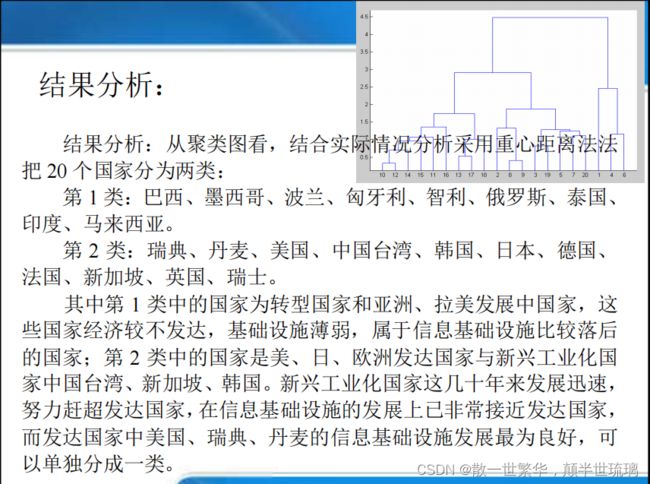
h=dendrogram(z2) %生成只有顶部n个节点的冰柱图
(谱系图)