LeetCode贪心经典题目(一)
文章目录
- 942. 增减字符串匹配
- 860. 柠檬水找零
- 179. 最大数
- 738. 单调递增的数字
- 452. 用最少数量的箭引爆气球
- 581. 最短无序连续子数组
- 659. 分割数组为连续子序列
- 646. 最长数对链
- 763. 划分字母区间
- 1029. 两地调度
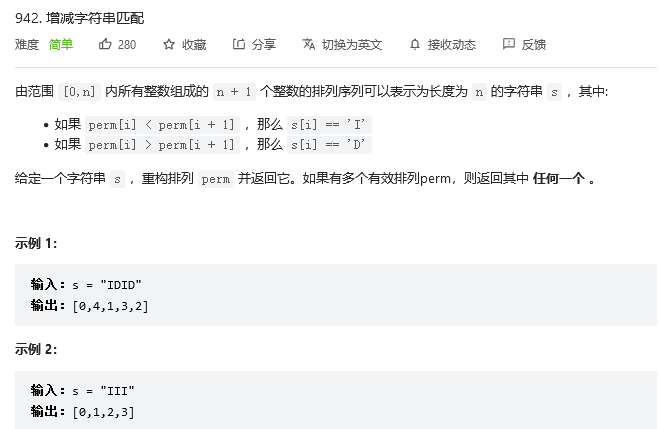
942. 增减字符串匹配
思路:遇到I,说明当前位置的数字比后面小,当前位置先选当前可以选的数字中最小的,接下来如果再遇到I,依然选择可以选择的数字中的最小的(之前已经选过的不再考虑);遇到D,说明当前位置的数字比后面大,优先选最大的,然后次大的…
最后遍历完之后,当前的最大值和最小值相等,将该值放在数组的最后一个位置即可(数组长度比字符串长度多1)
class Solution {
public int[] diStringMatch(String s) {
int n=s.length();
int[] ans=new int[n+1];
int i=0,j=0;
int min=0,max=n;
while(i<n){
if(s.charAt(i)=='I')
ans[i++]=min++;
else
ans[i++]=max--;
}
ans[n]=min;
return ans;
}
}
//O(n)
//O(1)
860. 柠檬水找零
https://leetcode.cn/problems/lemonade-change/

思路:当顾客给10元时,只能用5元进行找零;如果顾客用20元,则优先使用十元进行找零(贪心),因为5元的用处更多,不仅能找零给10元,也可以找零给20元
class Solution {
public boolean lemonadeChange(int[] bills) {
int cntFive=0,cntTen=0;
for(int bill:bills){
if(bill==5){
cntFive++;
}else if(bill==10){
cntFive--;//找零5元
if(cntFive<0)//找完之后为负数说明不能完成找零
return false;
cntTen++;
}else if(bill==20){
int x=15;
if(cntTen>0){//如果十元有 先用十元找零一部分
cntTen--;
x=5;
}
cntFive-=(x/5);//用5元进行找零
if(cntFive<0)//5元不够
return false;
}
}
return true;
}
}
//O(n)
//O(1)
179. 最大数
https://leetcode.cn/problems/largest-number/
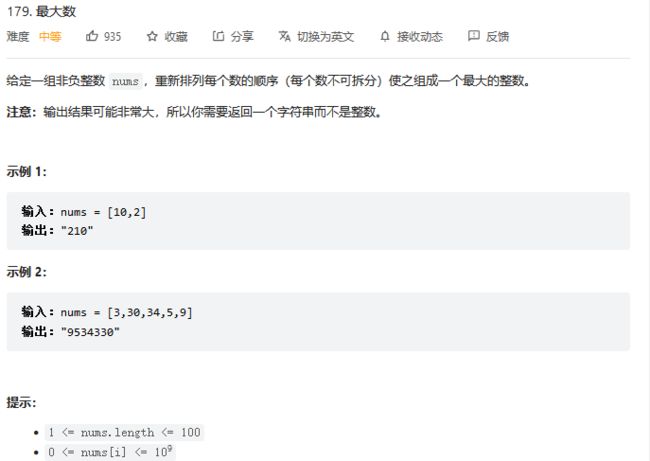
思路:如果数组有两个元素a,b,如果ab>ba, 则使用排列ab,反之则ba, 如果数组中有多个元素,依然采用这种方式,即对数组进行排序,但是排序的比较规则不再是往常的数值单纯比较,而是两个元素组合形成的数字的大小,如果证明这种排序得到的最后的排列是最大的?
假设真实解为:max 通过贪心法得到的解为ans 则一定有ans<=max, 而我们要证明ans==max, 剩下来只要正证明ans>=max即可
反证:假设ans
class Solution {
public String largestNumber(int[] nums) {
Integer[] numArr=new Integer[nums.length];
for(int i=0;i<nums.length;i++){
numArr[i]=nums[i];
}
Arrays.sort(numArr,(x,y)->{
int xx=10,yy=10;
while(xx<=x){
xx*=10;
}
while(yy<=y){
yy*=10;
}
//以【10,2】为例
//x=10 xx=100 xx中0的个数表示x是几位数
//y=2 yy=10 yy中0的个数表示y是几位数
//102=10*10+2=x*yy+y 210=2*100+10=y*xx+x
int num1=x*yy+y;
int num2=y*xx+x;
return num2-num1;//降序 如果a+b>b+a 则a排在b前面
});
if(numArr[0]==0)//最大的是0 后面都是0
return "0";//只需要返回1个0即可
StringBuilder sb=new StringBuilder();
for(int num:numArr){
sb.append(num);
}
return sb.toString();
}
}
738. 单调递增的数字
https://leetcode.cn/problems/monotone-increasing-digits/
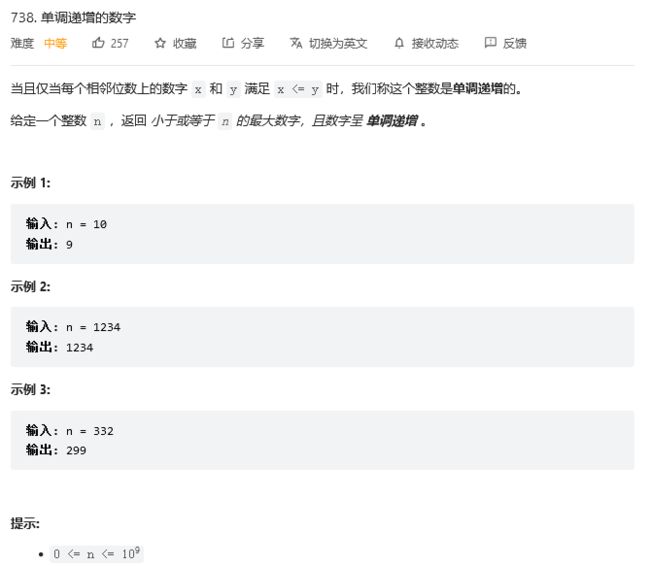
思路:若数字n本身就是递增的,则直接返回n即可;如果n不是递增的,需要寻找到开始不严格递增的转折点point,比如1234321,从4->3开始不严格递增;比如6666,下标0和下标1已经不满足严格递增了;
对于不是递增的数字n,为了获取最大值,转折点point之前的数字不变,point位置减一,point位置后的数字全部取最大数字9
1234321–>1234321->1233321->1233999
6666->5666->5999
class Solution {
public int monotoneIncreasingDigits(int n) {
String s=""+n;
int point=0;
boolean isAsc=true;
for(int i=0;i<s.length()-1;i++){
char c1=s.charAt(i);
char c2=s.charAt(i+1);
if(c1<c2){
point=i+1;
}
if(c1>c2){
isAsc=false;
break;
}
}
//point指向严格递增序列的最后一个数字
//比如1234321 point指向数字4
//分为3步处理:
//4前面的123不变 4减一变成3 4右边的321变成999
if(isAsc){
return n;
}else{
StringBuilder sb=new StringBuilder();
for(int i=0;i<point;i++){
sb.append(s.charAt(i));
}
sb.append(s.charAt(point)-'0'-1);
for(int i=point+1;i<s.length();i++){
sb.append('9');
}
return Integer.parseInt(sb.toString());
}
}
}
//O(n)
//O(n)
452. 用最少数量的箭引爆气球
https://leetcode.cn/problems/minimum-number-of-arrows-to-burst-balloons/

贪心的体现:射出的每支箭能够射掉最多的气球,怎样达到这个要求?将给出的位置数组按照结束位置排序,第一支箭从第一个气球的右端点射出,可以保证该支箭能够射掉最多的气球,直到某个气球的开始位置大于第一个气球的结束位置,重复这个过程
class Solution {
public int findMinArrowShots(int[][] points) {
//注意这里的排序比较方式不要使用o1[1]-o2[1] 数据太大会导致减法溢出
Arrays.sort(points,(o1,o2)->Integer.compare(o1[1],o2[1]));
//按照右端点排序 然后从最小的右端点射出去一只箭 保证这支箭能够射调最多的气球
int ans=1,end=points[0][1];
for(int[] point:points){
if(end<point[0]){
ans++;
end=point[1];
}
}
return ans;
}
}
//O(nlogn)
//O(logn)
581. 最短无序连续子数组
https://leetcode.cn/problems/shortest-unsorted-continuous-subarray/
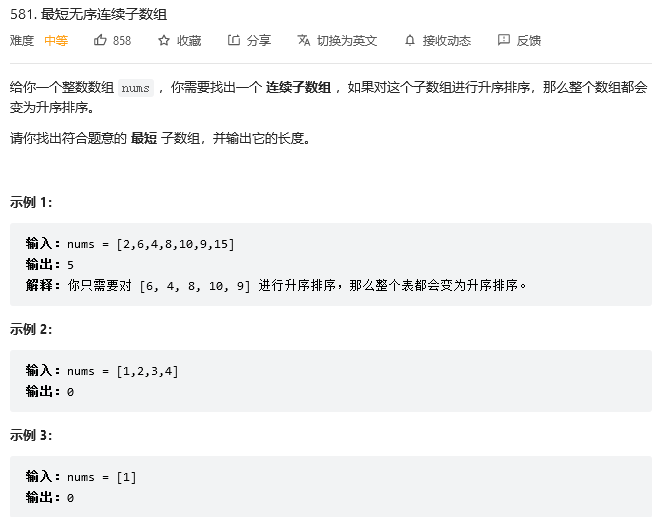
思路:
- 从前往后遍历,如果有
nums[i]>=max, 说明目前有序,更新当前的遍历到的最大值; 否则无序,记录无序的右边界R,可能会有多个R,最后选择最大的R作为需要调整的区间数组的有边界 - 从后往遍历,如果有
nums[i]<=min, 说明目前有序,更新当前的遍历到的最小值; 否则无序,记录无序的右边界L,可能会有多个L,最后选择最小的L作为需要调整的区间数组的有边界
举个特殊的例子,假设数组中的最大元素是10,而nums[0]=10, 则R会一直更新,直到n-1; 因为数组中最小的元素不在位置0,所以后面的L也会更新,直到L=0,因此整个数组需要重新排序,符合预期
class Solution {
public int findUnsortedSubarray(int[] nums) {
int left=-1,right=-1;
int n=nums.length;
int max=-10005,min=10005;
for(int i=0;i<n;i++){
if(nums[i]>=max){//当前元素nums[i]>=区间[0,i-1]内的元素 保持升序
max=nums[i];
}else{//nums[i]
right=i;
}
if(nums[n-i-1]<=min){//当前元素nums[n-i-1]<=区间[n-i,n]内的元素 保持升序
min=nums[n-i-1];
}else{//nums[i]>min 升序被打破 记录当前的元素位置
left=n-i-1;
}
}
return right==-1?0:(right-left+1);
}
}
//O(n)
//O(1)
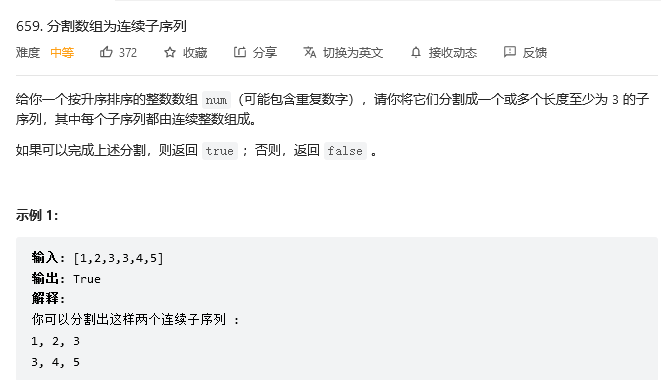
659. 分割数组为连续子序列
https://leetcode.cn/problems/split-array-into-consecutive-subsequences/
class Solution {
public boolean isPossible(int[] nums) {
HashMap<Integer,Integer> cnt=new HashMap<>();
HashMap<Integer,Integer> tail=new HashMap<>();
for(int num:nums){
cnt.put(num,cnt.getOrDefault(num,0)+1);
}
for(int num:nums){
if(cnt.getOrDefault(num,0)==0){
continue;
}
if(cnt.getOrDefault(num,0)>0&&tail.getOrDefault(num-1,0)>0){
cnt.put(num,cnt.get(num)-1);
tail.put(num-1,tail.get(num-1)-1);
tail.put(num,tail.getOrDefault(num,0)+1);
}else if(cnt.getOrDefault(num,0)>0&&cnt.getOrDefault(num+1,0)>0&&cnt.getOrDefault(num+2,0)>0){
cnt.put(num,cnt.get(num)-1);
cnt.put(num+1,cnt.get(num+1)-1);
cnt.put(num+2,cnt.get(num+2)-1);
tail.put(num+2,tail.getOrDefault(num+2,0)+1);
}else{
return false;
}
}
return true;
}
}
//O(n)
//O(n)
646. 最长数对链
https://leetcode.cn/problems/maximum-length-of-pair-chain/

思路:相当于是一个会议区间选择问题,如何选择可以得到较多的区间。先对这些区间按结束时间进行升序,然后开始选择,记上一个的结束位置是preEnd, 当前的区间开始位置是start, 如果start>preEnd, 则加入当前区间,并且更新preEnd=当前区间的结束位置
class Solution {
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs,(o1,o2)->o1[1]-o2[1]);
int ans=1;
int preEnd=pairs[0][1];
for(int i=1;i<pairs.length;i++){
int[] pair=pairs[i];
if(pair[0]>preEnd){
preEnd=pair[1];
ans++;
}
}
return ans;
}
}
//O(n)
//O(1)
763. 划分字母区间
https://leetcode.cn/problems/partition-labels/
思路:为了保证区间数最多,找到每个片段最小的结束下标,举个例子,第一个字符是a, 下一个a的位置是5, 那么需要遍历区间0-5,查看区间内的字符出现的位置会不会出现在5以外,如果出现还要继续寻找,直到找到一个区间结束位置end, 使得区间start-end内的字符的出现位置都在该范围内。
class Solution {
public:
vector<int> partitionLabels(string s) {
unordered_map<char,int> pos;
vector<int> ans;
int n=s.size();
for(int i=0;i<n;i++){
pos[s[i]]=i;
}
int start=0,end=0;
for(int i=0;i<n;i++){
end=max(end,pos[s[i]]);//遍历区间过程中 区间内的字符可能会出现在更远的位置
if(i==end){//i==end说明找到一个区间
ans.push_back(end-start+1);
start=end+1;//下一个片段的开始位置
end=pos[s[start]];//下一片段开始字符的最后出现的位置
}
}
return ans;
}
};
//O(n)
//O(c) c=26
1029. 两地调度
https://leetcode.cn/problems/two-city-scheduling/

思路:假设已经确定了N人去B,然后现在又想让这N人去A,原本去B的每个人的费用是costb, 现在去A的每个人费用是costa, 对于每个人而言,省下来的钱是costb-costa, 即costb-costa越大越好,也即costa-costb越小越好, 所以对数组按costa-costb的差值进行排序,差值最小的N人去A,剩下的人去B
class Solution {
public int twoCitySchedCost(int[][] costs) {
//Arrays.sort(costs,(o1,o2)->(o2[1]-o2[0])-(o1[1]-o1[0]));
//按costb-costa的差值进行降序也可以
Arrays.sort(costs,(o1,o2)->(o1[0]-o1[1])-(o2[0]-o2[1]));//按costa-costb的差值进行升序
int sum=0;
int index=0;
for(int[] cost:costs){
if(index<costs.length/2){//前一半人去a城市
sum+=cost[0];
}else{//后一半人去b城市
sum+=cost[1];
}
index++;
}
return sum;
}
}
//O(nlogn)
//O(logn)