c语言贪心算法最小生成树,贪心算法4-最小生成树(Prim算法)
1.问题分析
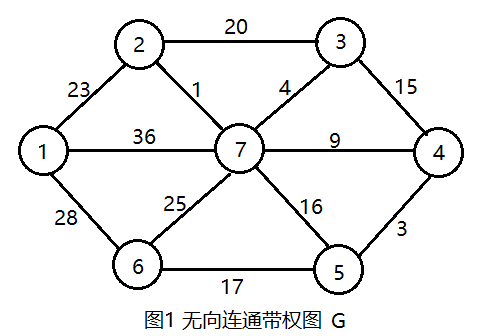
在一个有n个节点的无向连通图G = (V, E)中,V表示顶点集,E表示边集。只需n-1条边就可以使这个图连通,n-1条边要想保证图连通,就必须不含回路,所以我们只需要找出n-1条权值最小且无回路的边即可。
需要明确几个概念:
生成子图:选中一些边和所有顶点组成的图,称为原图的生成子图。
生成树:如果生成子图恰好是一棵树,称为生成树。
最小生成树:权值之和最小的生成树,称为最小生成树。
2.算法分析
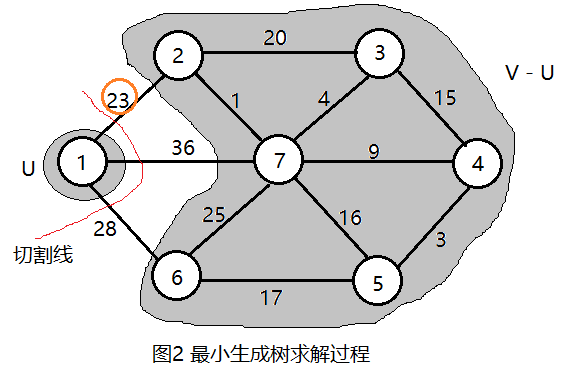
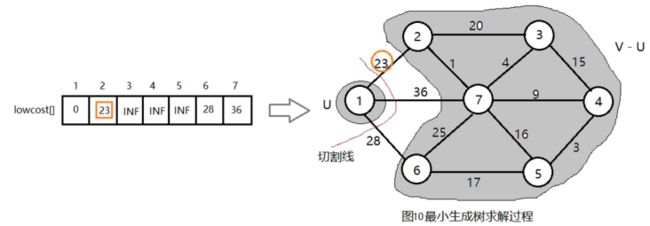
为了在最小生成树的生成过程中,不产生环路,我们可以使用“切割法”。具体来说,在生成树的过程中,我们把已经在生成树的节点看成一个集合,把剩下的节点看作另一个集合,在这两个集合之间画一条切割线,从切割线经过的边上选出一条取值最小的作为新加入的边,可以形象地把这种方法称为“切割法”。
首先任选一个节点,如1号节点,把它放在U中,U = {1},那么剩下的节点即V - U = {2,3,4,5,6,7},V是图的所有顶点集合。如图2所示。
现在在连接两个集合(U和V-U)的边中找出权值最小的,通过画切割线可以很快找到节点1和节点2之间的边权值最小,选中这条边,把2号节点加入U = {1, 2}, V - U = {3, 4, 5, 6}。
再按照上述操作在连接两个集合(U和V-U)的边中找出权值最小的边,如图3所示。如此下去,直到U = V结束。
这个就是Prim算法,1957年由美国计算机科学家Robert C.Prim发现的。通过观察可以发现,Prim算法的贪心策略是:每次选取连接U和V-U的所有边中的最短边。
3.算法设计
算法设计的步骤如下所示:
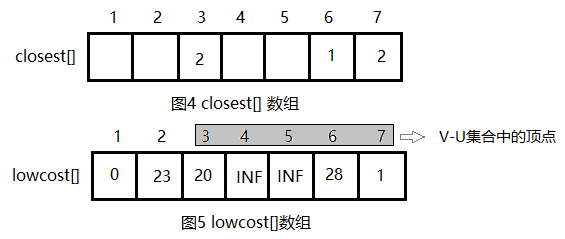
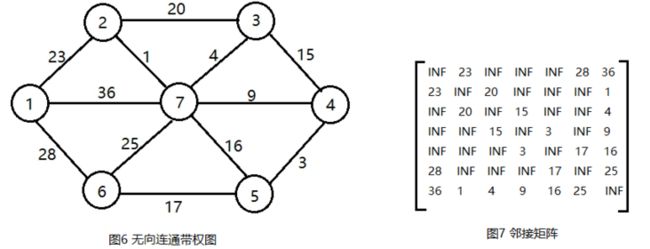
步骤1:设计数据结构。用带权邻接矩阵C存储图G,bool数组s[],如果s[i] = true,说明顶点i已加入集合U,如图2所示。还有一个问题就是,从图上我们可以很直观地找出连接两个集合中的权值最小的边,但是在程序中如果穷举这些边就会很麻烦。在单源最短路径,我们只需要维护一个源点到其它点的最短距离数组dist[]即可,但是这里显然不行,我们需要维护的是V-U中的点到U的最短距离,需要两个数组,closest[j]表示V-U中的节点j到集合U中的最临近点,lowcost[j]表示这两个点之间边的权值。对于图2的求解过程,对应的closest[]和lowcost[]如下图所示:
只需要在V-U集合找lowcost[]值最小的顶点即可。
步骤2:初始化。令集合U={u},并初始化cloest[],lowcost[]和s[]。
步骤3:在V-U集合中找lowcost最小的节点t,将节点t加入集合U。
步骤4:如果集合V-U为空,算法结束。
步骤5:对集合V-U中的所有顶点j,更新其lowcost[]和closest[]。由于此时t已经是U中的节点,但它和U-V中的一些节点有连接,因此需要更新当它加入U时而引起的连接两个集合的权值最小的边的变化情况,更新公式为:if(c[t][j] < lowcost[j]) {lowcost[j] = c[t][j] ; closest[j] = t;},转步骤3。
按上述步骤,最终可以得到一棵权值之和最小的生成树。
4.算法图解
(1)数据结构
(2)初始化
假设u=1, 令集合U = {1}, V - U = {2,3,4,5,6,7},s[1] = true,初始化closest[]:除了1号节点外其余节点均为1,表示V-U中的顶点到集合U的最临近点都为1,因为它们现在在U中还看不到其它节点。lowcost[]:1号节点到V-U中的节点的边的权值,直接读取邻接矩阵第一行就好。初始化结果如下图所示。
(3)找最小
在集合V-U={2,3,4,5,6,7}中,依照贪心策略寻找V-U集合中lowcost最小的顶点t,如下图所示。
(4)加入集合U
令集合U = {1,2}, V - U = {3,4,5,6,7}, s[2] = true。
(5)更新
将2号节点加入集合U,和它邻接集合V-U中的节点是3和7。更新节点3和7:
c2 = 20 < lowcost[3] = INF,更新lowcost[3] = 20,同时更新closest[3] = 2;
c2 = 1 < lowcost[7] = 36, 更新lowcost[7] = 1,同时更新closest[7] = 2;更新后的结果如下图所示。
(6)找最小
在集合V-U={3,4,5,6,7}中,依照贪心策略寻找V-U集合中lowcost最小的顶点t,如下图所示。
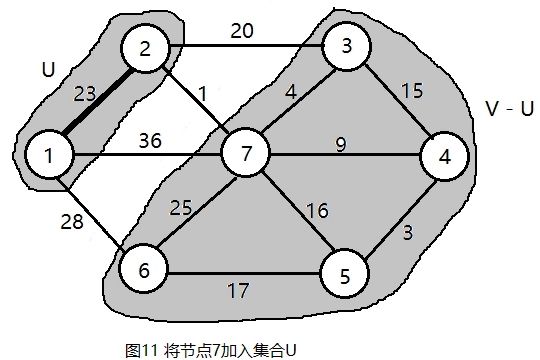
(7)加入集合U
令集合U = {1,2,7}, V - U = {3,4,5,6}, s[7] = true。
(8)更新
将7号节点加入集合U后,和它邻接集合V-U中的节点是3,4,5,6。更新:
c7 = 4 < lowcost[3] = 20, 更新lowcost[3] = 4, 同时更新closest[3] = 7;
c7 = 9 < lowcost[4] = INF, 更新lowcost[4] = 9, 同时更新closest[4] = 7;
c7 = 16 < lowcost[5] = INF, 更新lowcost[5] = 16, 同时更新closest[5] = 7;
c7 = 25 < lowcost[6] = 28, 更新lowcost[6] = 25, 同时更新closest[6] = 7;
更新后的结果如下图所示。
(9)找最小
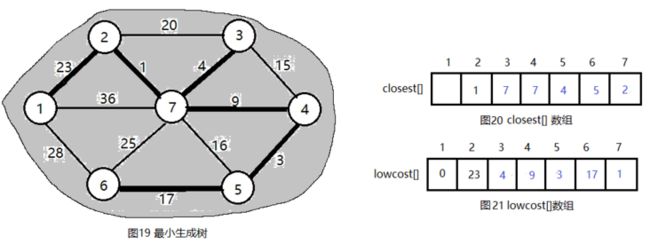
(10)继续这样处理,最终得到结果如下图。
(画不动了,太累了。。。)
5.代码片段展示
(1)初始化
// u表示最先加入集合U中的节点编号
s[u] = true;
for (int i = 1; i <= n; i++) {
// 初始化lowcost[],closest[]和s[]
if (i != u) {
lowcost[i] = c[u][i];
closest[i] = u;
s[i] = flase;
}
else
lowcost[i] = 0;
}
(2)在集合V-U中寻找距离集合U最近的顶点t
int tmp = INF, t = u;
for (int j = 1; j <= n; j++) {
if (!s[j] && (lowcost[j] < tmp)) { //!s[j]表示j节点V-U集合中
t = j;
tmp = lowcost[j];
}
}
// 找不到,跳出循环
if (t == u) break;
(3)更新lowcost和closest数组
s[t] = true; // 将t加入集合U
for (int j = 1; j <= n; j++) {
if ((!s[j]) && (c[t][j] < lowcost[j])) {
lowcost[j] = c[t][j];
closest[j] = t;
}
}
6.代码实现
// 基于Prim算法实现最小生成树
#include
#include
const int INF = 1e7;
using namespace std;
vector> Init() {
int n, m;
cout << "请输入带权无向图的定点数和边数(以空格隔开):" << endl;
cin >> n >> m;
vector> graph(n+1, vector(n+1, INF));
cout << "请依次输入" << m << "条边的开始节点,结束节点,权值(以空格隔开):" << endl;
int start, end, wet;
for (int i = 0; i < m; i++) {
cin >> start >> end >> wet;
graph[start][end] = wet;
graph[end][start] = wet;
}
return graph;
}
int Prim(vector>& c, int u) {
int n = c.size() - 1;
// 定义数据结构lowcost[],closest[],s[]
vector lowcost(n+1);
vector closest(n+1);
vector s(n+1);
/// 1.初始化lowcost[],closest[],s[]
s[u] = true;
for (int i = 1; i <= n; i++) {
if (i != u) {
lowcost[i] = c[u][i];
closest[i] = u;
s[i] = false;
}
else
lowcost[i] = 0;
}
// n个节点之间需要找最短路径n-1次
for (int i = 0; i < n-1; i++) {
// 2.找最小
int tmp = INF, t = u;
for (int j = 1; j <= n; j++) {
if (!s[j] && (lowcost[j] < tmp)) { //!s[j]表示j节点V-U集合中
t = j;
tmp = lowcost[j];
}
}
// 找不到,跳出循环
if (t == u) break;
// 将t加入集合U
s[t] = true;
// 3.更新
for (int j = 1; j <= n; j++) {
if ((!s[j]) && (c[t][j] < lowcost[j])) {
lowcost[j] = c[t][j];
closest[j] = t;
}
}
}
// 4.打印最终结果
int totalcost = 0;
cout << "lowcost[]数组:";
for (int i = 1; i <= n; i++) {
cout << lowcost[i] << " ";
totalcost += lowcost[i];
}
cout << endl;
cout << "closest[]数组:";
for (int i = 1; i <= n; i++) {
cout << closest[i] << " ";
}
cout << endl;
return totalcost;
}
// test main()
int main() {
vector> graph = Init();
int weight = Prim(graph, 1); // 1表示从1开始找
cout << "\n最小生成树总的花费是:" << weight << endl;
}
7.实验结果
请输入带权无向图的定点数和边数(以空格隔开):
7 12
请依次输入12条边的开始节点,结束节点,权值(以空格隔开):
1 2 23
1 6 28
1 7 36
2 3 20
2 7 1
3 4 15
3 7 4
4 5 3
4 7 9
5 6 17
5 7 16
6 7 25
lowcost[]数组:0 23 4 9 3 17 1
closest[]数组:0 1 7 7 4 5 2
最小生成树总的花费是:57
D:\projects\test\x64\Release\test.exe (进程 1788)已退出,返回代码为: 0。
8.算法优化
显然,Prim算法的时间复杂度为O(n^2),同单源最短路径,哈夫曼编码类似,都可以通过在“找最小”的步骤引入优先队列,可以使找最小的操作的时间复杂度降为O(logn),总的时间复杂度降为O(nlogn),Prim算法用优先队列比较简单,如前面几个贪心算法那样,只需构造一个结构体来存储节点相关信息,重写节点的排序规则就可以了,这里就不再进行代码演示,有疑问的看官可以参考贪心算法二和三的算法优化相关部分讲解,也可以直接留言提问。
Prim算法的讲解就到这里,各位看官不要走开,请继续关注下一讲贪心算法三--最小生成树(Kruskal算法)~~~
我是lioney,年轻的后端攻城狮一枚,爱钻研,爱技术,爱分享。
个人笔记,整理不易,感谢阅读、点赞和收藏。
文章有任何问题欢迎大家指出,也欢迎大家一起交流后端各种问题!