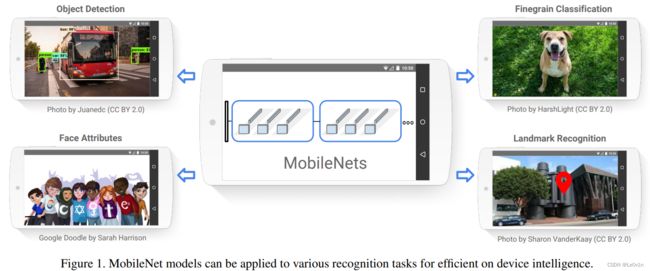
MobileNet系列 (v1 ~ v3) 理论讲解

1. MobileNet v1

MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications

论文地址：https://arxiv.org/abs/1704.04861
PyTorch官方实现代码：https://pytorch.org/vision/stable/models.html#classification

1.0 MobileNet v1的设计动机

传统CNN网络的运算量大，对内存需求大，导致无法在移动设备以及嵌入式设备上运行。

• VGG-16模型大小大概为490 MB
• ResNet-152模型权重大小为644 MB

这么大的磁盘占用量（权重文件越大代表模型需要的算力越高）基本上不能在移动设备和嵌入式设备商使用，因此亟需一种轻量型模型，扩大CNN的使用范围。

---

MobileNet网络是由Google团队在2017年提出的，专注于移动端和嵌入式设备中的轻量型CNN网络。相比传统CNN网络而言，MobileNets网络在准确率小幅度降低的前提下大大减少了模型的参数量和运算量。

相比VGG-16，MobileNet v1准确率减少了0.9%，但模型参数只有前者的$\frac{1}{32}$。

1.1 DWConv —— 深度卷积

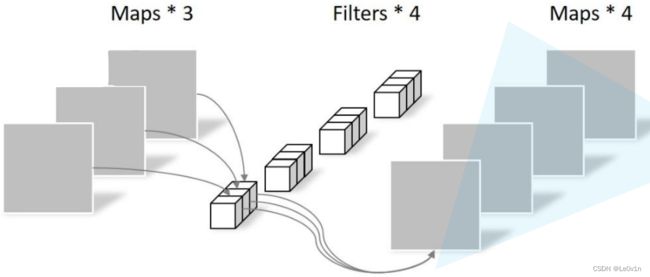
1.1.1 普通卷积示意图

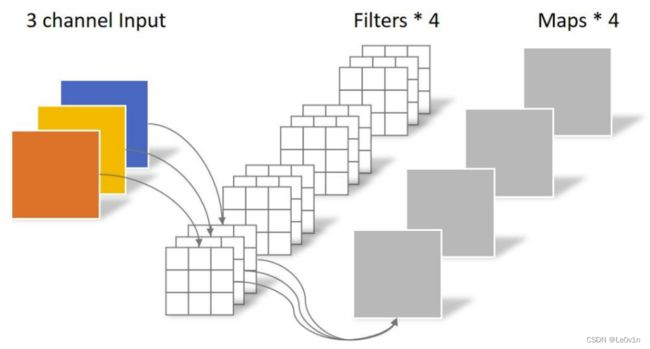
输入是一个深度为3的特征图，使用4个卷积核对其进行卷积运算。为了可以运算，每个卷积核的深度也要等于3。对于每一个卷积核，每个channel求出一个特征图，再$\oplus$得到一个clip，4个卷积核得到4个clip，再将这些clip进行concat处理，就得到了最终的输出特征图。

---

传统卷积（普通）卷积的特性：

• 卷积核channel=输入特征图channel
• 输出特征图channel=卷积核个数

1.1.2 深度卷积示意图

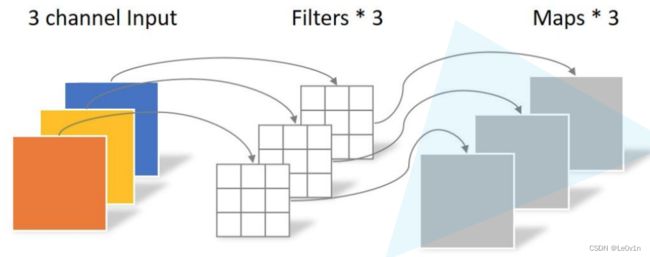
在DWConv中，每个卷积核的深度都是为1的（并不像传统卷积那样，卷积核的深度与输入特征图的深度相同），每个卷积核只负责与输入特征图的一个channel（clip）进行卷积运算，再得到输出特征图的一个clip，最终将所有得到的clip进行concat得到最终的输出特征图。

DWConv（深度卷积）的特性：

• 卷积核channel=1
• 输入特征图channel=卷积核个数=输出特征图channel -> 经过DWConv之后，特征图的深度是不会发生变化的。

这里说的"特征图的深度是不会发生变化的"是指正确使用了DWConv（而非写错导致成了分组卷积）

---

为了验证DWConv是否真的必须输出输出通道数相等，我们做一个实验，代码如下：

import torch


class MobileNet(torch.nn.Module):
    def __init__(self):
        super(MobileNet, self).__init__()

        # 输出通道数为3，groups=3
        """
        	深度卷积
        """
        self.dwconv_1 = torch.nn.Sequential(torch.nn.Conv2d(in_channels=3,
                                                            out_channels=3,
                                                            kernel_size=(3, 3),
                                                            stride=(1, 1),
                                                            padding=(1, 1),
                                                            groups=3))
        """
        输出通道数为12，groups=3
            没有问题，相当于是分组卷积
        """
        self.dwconv_2 = torch.nn.Sequential(torch.nn.Conv2d(in_channels=3,
                                                            out_channels=12,
                                                            kernel_size=(3, 3),
                                                            stride=(1, 1),
                                                            padding=(1, 1),
                                                            groups=3))
        """
        输出通道数为12，groups=12
            在定义网络时就会报错: ValueError: in_channels must be divisible by groups
        """
        self.dwconv_3 = torch.nn.Sequential(torch.nn.Conv2d(in_channels=3,
                                                            out_channels=12,
                                                            kernel_size=(3, 3),
                                                            stride=(1, 1),
                                                            padding=(1, 1),
                                                            groups=12))

我们可以发现，group一定要能被inp整除，如果：

• inp / group = 1：深度卷积
• inp / group = int：分组卷积

深度卷积本质上是分组卷积的一种特殊情况

1.1.3 深度可分离卷积

深度可分离卷积由两部分组成：

1. 深度卷积 -> 特征提取
2. 点卷积（逐通道卷积） -> 改变channel

---

点卷积如下所示：

点卷积卷积核的深度与输入特征图深度相同，与普通卷积不同的是，点卷积的卷积核大小为1。

1.1.4 深度可分离卷积与常规卷积参数量对比

我们首先计算常规卷积的计算量。

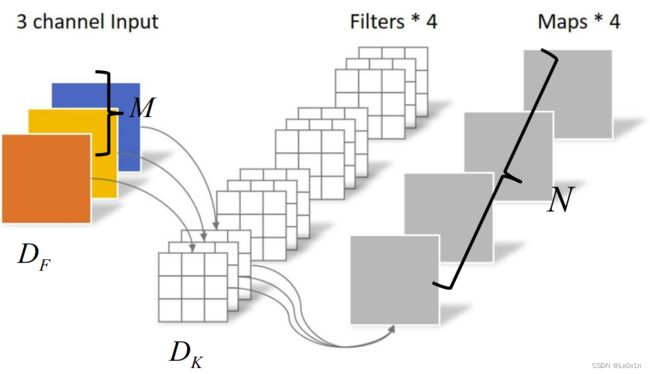
其中：

• $D_F$输入特征图的高和宽
• $D_K$：卷积核的大小
• $M$：输入特征图的深度
• $N$：输出特征图的深度（卷积核的个数）

对于普通卷积，其计算量如下（默认stride为1）：

$$\text{FLOPs}=\underset{卷积核大小}{D_K\cdot D_K}\cdot \underset{卷积核深度}{M}\cdot \underset{卷积核个数}{N}\cdot \underset{输入特征图的尺寸}{D_F\cdot D_F}$$

---

深度可分离卷积参数量计算如下：
$$\begin{array}{rl}\text{FLOPs}& =\underset{\text{DWConv}}{\underset{卷积核的大小}{D_K\cdot D_K}\cdot \underset{卷积核深度}{M}\cdot \underset{输入特征图的尺寸}{D_F\cdot D_F}}+\underset{卷积核的大小}{1\cdot 1}\cdot \underset{卷积核深度}{M}\cdot \underset{卷积核个数}{N}\cdot \underset{输入特征图的尺寸}{D_F\cdot D_F}\\ & =\underset{\text{DWConv}}{\underset{卷积核的大小}{D_K\cdot D_K}\cdot \underset{卷积核深度}{M}\cdot \underset{输入特征图的尺寸}{D_F\cdot D_F}}+\underset{卷积核深度}{M}\cdot \underset{卷积核个数}{N}\cdot \underset{输入特征图的尺寸}{D_F\cdot D_F}\end{array}$$

---

深度可分离卷积参数量占常规卷积参数量的大小：

$$\begin{array}{rl}rate& =\frac{\text{DWConv + PWConv}}{\text{Normal Conv}}\\ & =\frac{D_K^2\cdot M\cdot D_F^2+M\cdot N\cdot D_F^2}{D_K^2\cdot M\cdot N\cdot D_F^2}\\ & =\frac{M\cdot D_F^2(D_K^2+N)}{D_K^2\cdot M\cdot N\cdot D_F^2}\\ & =\frac{D_K^2+N}{D_K^2\cdot N}\\ & =\frac{1}{D_K^2}+\frac{1}{N}\\ & =\frac{1}{3^2}+\frac{1}{N}\\ & =\frac{1}{9}+\frac{1}{N}\end{array}$$

其中$N$为卷积核的个数，卷积核越大$\frac{1}{N}$越小。故在理论上，深度可分离卷积的计算量为普通卷积的$\frac{1}{9}$ ~ $\frac{8}{1}$倍。

这里只是理论上的，计算量并不能说明一切，因为3×3卷积已经被优化过了，所以深度可分离卷积并不会比普通卷积快多少，而且深度可分离卷积的特征提取能力弱于普通卷积。

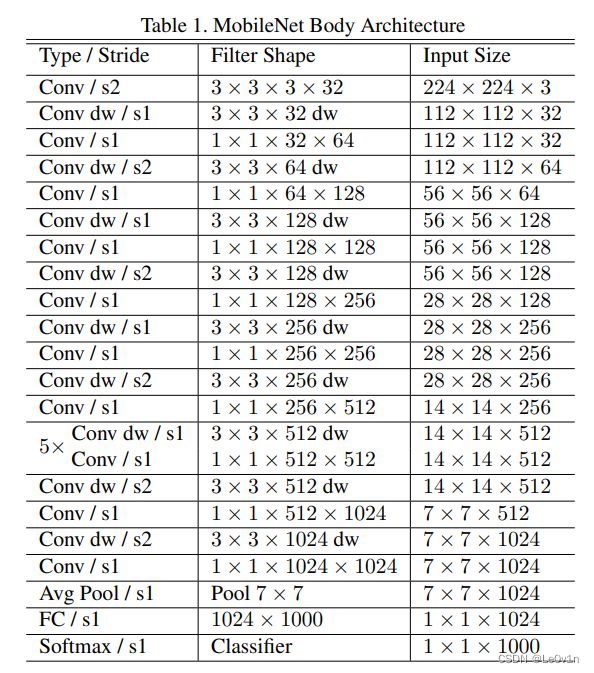
1.2 MobileNet v1的网络结构

MobileNet v1的网络结构类似于VGG，并没有使用残差结构，只是很朴实的串行结构。

1.3 MobileNet v1与其他网络的参数量对比

1.4 超参数 —— 乘宽系数$\alpha$和输入图片分辨率系数$\beta$

1.4.1 乘宽系数$\alpha$

$\alpha$为卷积核个数的倍率 —— 控制特征图通道数大小。

可以看到，当$\alpha$减少时，模型的准确率在降低，但计算量和可训练参数数量在减少。

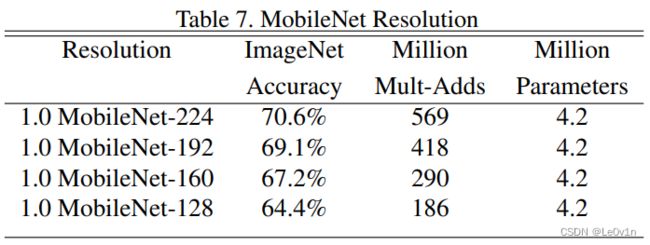
1.4.2 输入图片分辨率系数$\beta$

当输入图片大小减少时，模型的准确率在降低，但计算量和可训练参数数量在减少。

1.5 MobileNet v1实际使用时遇到的问题

在实际使用时，很多人发现，MobileNet v1的很多DWConv在训练完后，部分卷积核是废掉的（一片漆黑，参数等于0，没有学习到东西）。

针对这个问题，MobileNet v2会进行改善。

2. MobileNet v2

MobileNetV2: Inverted Residuals and Linear Bottlenecks

论文地址：https://arxiv.org/abs/1801.04381

2.0 动机

MobileNet v2网络是由Google团队在2018年提出的，相比MobileNet v1，其准确率更高、模型更小。

---

网络的亮点：

1. Inverted Residuals（逆残差结构）
2. Linear Bottleneck

2.1 Inverted Residual Block（逆残差模块）

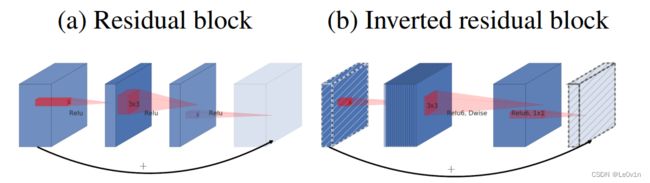
2.1.1 ResNet中的残差模块

1. 先使用1×1卷积对特征图的channel进行压缩（减少运算量）
2. 通过3×3卷积提取特征
3. 使用1×1卷积扩充channel

这样就形成了两头大中间小的瓶颈结构。

使用的激活函数为ReLU激活函数

2.1.2 MobileNet v2中的逆残差模块

1. 先使用1×1卷积对特征图的channel进行升维
2. 通过卷积核大小为3×3的DWConv进行特征提取
3. 通过1×1卷积对特征图进行降维处理

使用的激活函数为ReLU6激活函数

2.2 ReLU6激活函数

表达式：

$$\text{ReLU6}(x)=\min (\max (x,0),6)$$

图像：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams

plt.figure(figsize=(10, 6))
config = {
    "font.family": 'Times New Roman',
    "font.size": 20,
    "mathtext.fontset": 'stix',
    "font.serif": ['Times New Roman'],
}
rcParams.update(config)

# ReLU
x = np.linspace(-3, 8, 100)
ReLU = np.maximum(0, x)
plt.plot(x, ReLU, label="ReLU")

# ReLU6
x = np.linspace(-3, 8, 100)
ReLU6 = np.minimum(np.maximum(0, x), 6)
plt.plot(x, ReLU6, label="ReLU6")
# 刻度线
plt.plot([0, 0], [8, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 8], [0, 0], c="k", ls=":", lw=1.5)
plt.title("ReLU6")

# 刻度线
plt.plot([0, 0], [1.1, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.legend()
plt.tight_layout()
plt.show()

2.3 Linear Bottleneck

不像ResNet的Bottleneck那样，ResNet最后一个1×1卷积后是一个ReLU激活函数，而MobileNet v2中的Residual Bottleneck在最后一个1×1卷积后没有使用ReLU激活函数，而是使用了一个Linear（即不使用激活函数）

---

图1：嵌入高维空间的低维流形的ReLU变换示例。在这些示例中，使用随机矩阵T和ReLU将初始螺旋嵌入到n维空间，然后使用T投影回2D空间−在上面的例子中，n=2，3导致信息丢失，其中流形的某些点彼此塌陷，而对于n=15到30，变换是高度非凸的。

在原文中，逆残差的最后一个1×1卷积中，使用的是线性的激活函数（即不使用激活函数）而不是ReLU。作者做了一个实验：输入是一个二维的矩阵，它的channel=1。分别采用不同维度的matrix $T$将其进行变换，变换到一个更高的维度上。然后使用ReLU激活函数得到它的输出值。之后再使用 $T$ 矩阵的逆矩阵，将输入矩阵还原回2D 矩阵。当Matrix $T$的维度 $n=2,3$ 时（output/dim=2, Output/dim=3），它俩丢失了很多信息。但随着Matrix $T$的维度$n$逐渐增加，丢失的信息越来越少了。这个实验证明了：

• ReLU激活函数对低维特征信息造成大量损失
• 而对高维特征信息造成的损失很小。

又因为在逆残差结构中，是两边细中间粗的瓶颈结构，因此经过最后一个1×1卷积降维后就是一个低维的特征图了，此时再使用ReLU激活函数，那么会造成很大的特征信息损失。

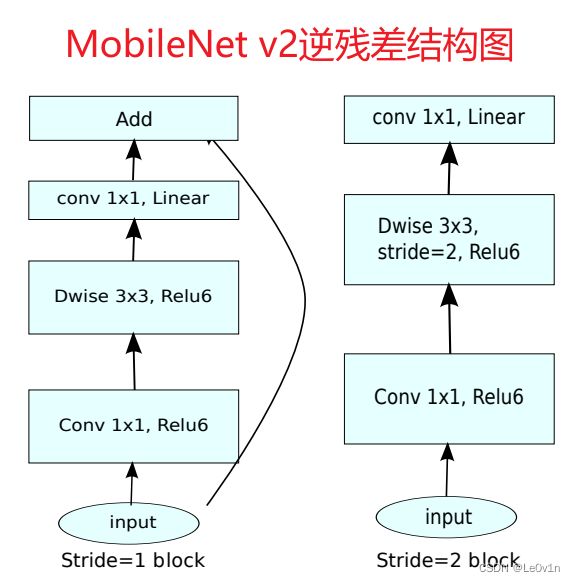
2.4 逆残差结构图

其中：

• $t$为宽展因子：第一个1×1卷积核的个数（输出channel）为$t\times k$。
• $k^{\prime }$为我们期望的输出通道数。

论文中是这样说的：只有当stride=1时才有shortcut，当stride=2时没有shortcut分支。但经过霹雳吧啦Wz看PyTorch实现的源码后发现：论文中的表述是有误的。正确的表述应该为：当stride=1且输入特征矩阵与输出特征矩阵的shape相同时才有shortcut分支（shape不同，shortcut分支如果没有其他部件，那么shortcut会报错）。

2.5 MobileNet v2网络架构

表2:MobileNet v2：每一行描述一个或多个相同(步长)层的序列，重复 $n$ 次。同一序列中的所有层具有相同数量的输出通道 $c$。每个序列的第一层有一个步幅 $s$，其他所有使用步幅$1$。所有的空间卷积都使用3 × 3核。如表1所示，扩展因子 $t$ 总是应用于输入大小。

其中：

• $t$为扩展因子，即第一个1×1卷积要将channel提升多少倍。
• $c$为输出特征图的channel，即$k^{\prime }$
• $n$为Block重复的次数
• $s$为步长。需要注意的是，这里的$s$只代表每一个Block第一个Bneck的步长，其他的Bneck步长都是为1的。
• $k$为类别数

• 一个Block由一系列Bneck组成
• 第一个Block的$t=1$则第一个1×1卷积不会对特征图的channel进行扩充的，但在PyTorch官方实现中，这个Block直接不使用1×1卷积，直接使用DWConv（因为这个1×1卷积既没有起到升维作用，也没有起到降维作用，而且它的特征提取能力几乎为0，所以直接去掉提高速度了）
• 最后一层是一个1×1卷积层，其实就是一个FC层（确切来说是功能和FC是一样的）

2.6 性能对比

2.6.1 分类任务

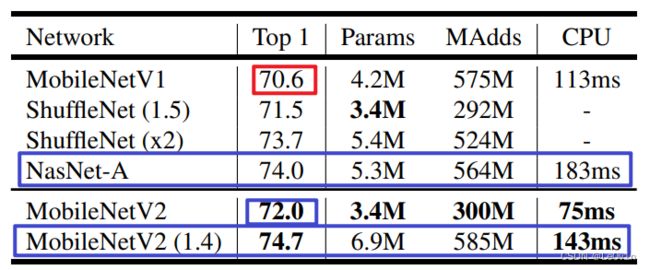
表4：ImageNet的性能，不同网络的比较。按照行动的惯例，我们计算了乘法运算的总数。在最后一栏，我们报告了谷歌Pixel 1手机（使用TF-Lite）单个大核心的运行时间，单位为毫秒（ms）。我们不报告ShuffleNet的数字，因为还不支持高效的分组卷积和洗牌。

可以看到，MobileNet v2相比MobileNet v1而言，实现了更高的精度和更快的速度。相对NasNet-A而言，MobileNet v2的速度快了一倍多（13.3 FPS），但精度不如NasNet-A。因为本文还提供了MobileNet v2 (1.4)，即乘宽系数为1.4的MobileNet v2模型，该模型的精度比NasNet-A要高，且速度比NasNet-A要快（7 FPS）。

一定要学习人家这种比较方式：

• 如果精度不够SOTA，那么就想办法提升到SOTA，此时再比较其他参数（这样才能说明我们的模型在相同精度下的优势）
• 如果精度不够SOTA，此时一味地强调速度，那么很难不让人怀疑，你的网络如果达到同样的精度SOTA，速度是否还能SOTA。

2.6.2 目标检测

表5：比较SSD和SSDLite配置MobileNetV2并对80个类进行预测的大小和计算成本。

SSDLite即为将部分常规卷积替换为深度可分离卷积后的SSD网络，可以很明显的看到，此时网络的参数量和加法运算大幅度减少。

---

表6：MobileNetV2 +SSDLite和其他实时检测器在COCO数据集物体检测任务上的性能比较。MobileNetV2 + SSDLite以更少的参数和更小的计算复杂度实现了有竞争力的准确性。所有模型都在trainval35k上训练，并在test-dev上评估。SSD/YOLOv2的数字来自[35]。运行时间是针对谷歌Pixel 1手机的大核心报告的，使用的是TF-Lite引擎的内部版本。

将MobileNet v2和SSD联合使用。首先将SSD的部分卷积替换为深度可分离卷积，称为SSDLite。将MobileNet v2当作前置网络，这样就形成了MNet v2 + SSDLite。新的网络与SSD300、SSD512、YOLO v2、MobileNet v1 + SSDLite的模型而言，准确率虽然不如SSD300和SSD512，但是比YOLO v2的效果要好。这里比较让人费解的是，比MNet V1 + SSDLite的准确率要低，但是速度要更快（5 FPS）。

3. MobileNet v3

Searching for MobileNetV3

论文地址：https://arxiv.org/abs/1905.02244

---

MobileNet v3的核心点：

1. 更新了Block（bneck）：在v2的逆残差结构上进行了简单的改动
2. 使用了NAS搜索参数的技术
3. 重新设计耗时层结构：对网络每一层的推理时间进行了分析，针对某些耗时的层结构进行了进一步的优化

3.1 v3相比v2在性能上的提升

与MobileNetV2相比，MobileNetV3-Large在ImageNet分类上的准确性提高了3.2%，同时延迟降低了20%。与延迟相当的MobileNetV2模型相比，MobileNetV3-Small的准确性提高了6.6%。MobileNetV3-Large的检测速度超过25%，在COCO检测上与MobileNetV2的精度基本相同。MobileNetV3-Large LRASPP比MobileNetV2的R-ASPP快34%，而Cityscapes分割的准确度也差不多。

在摘要中作者提到，v3的Large版本相对v2而言，在ImageNet Classificiation任务上准确率提升3.2%，延迟降低了20%。

3.2 MobileNet v3与其他网络在ImageNet上性能对比

表3. Pixel系列手机的浮点性能（P-n表示Pixel-n手机）。所有的延迟都是以毫秒(ms)为单位的，并使用一个批处理大小(Batch Size)的单一大核心来测量。在ImageNet上的准确度排名第一。

• v3-Large 1.0的Top-1准确率为75.2，对比v2的1.0版本而言，Top-1为72%，提升了3.2%。推理速度也有提升。v3-Large对比v2-1.0不仅准确率更高，而且速度更快。
• v3-Small版本相比v2的小版本（v2-0.35）也有6.6%的提升，而且速度也更低一些。

3.3 v3中的Bneck

与v2的中Bottleneck不同的是：

1. 加入了SE模块
2. 更新了激活函数

v2中的逆残差

①通过1×1卷积进行升维（-> BN -> ReLU6）；②使用3×3 DWConv（-> BN -> ReLU6）；③1×1卷积进行降维（-> BN）。当stride=1且输入输出shape相同时使用shortcut连接。

v3中的逆残差

1. 加入了SE模块

首先介绍SE注意力机制：①对特征图的每一个channel进行池化处理；②通过两个FC得到输出的向量（channel -> channel / 4 -> channel）；③将注意力矩阵与输入特征图相乘，实现特征图通道加权。

两个FC所使用的的激活函数不同：FC1 (ReLU) -> FC2 (H-sigmoid)

2. 更新了激活函数

图中的NL表示非线性激活层，因为不同层所使用的激活函数不同，所以图中没有给出一个明确的激活函数名称。

• Bneck中最后的1×1降维卷积并没有使用NL（可以理解为和v2一样，使用的是Linear激活）
• 线性激活的表达式为$y=x$，即没有使用激活函数

---

v3 Bneck的流程如下：

1. 使用1×1卷积进行升维（-> BN -> NL）；
2. 使用3×3 DWConv进行特征提取（-> BN -> NL）；
3. 使用SE模块对特征图通道维度加权（x -> AvgPool -> FC -> ReLU -> FC -> H-sigmoid -> x $\otimes$ M）
4. 使用1×1卷积进行降维（-> BN）

3.4 重新设计耗时层结构

关于这部分，原论文主要讲了2个部分：

1. 减少第一个卷积层的卷积核个数（32 -> 16）
2. 精简Last Stage

3.4.1 第一层卷积核个数 32 -> 16

我们能够将卷积核的数量减少到16个，同时保持与使用ReLU或swish的32个卷积核相同的精度。这又节省了2毫秒(ms)和1000万Adds运算。

3.4.2 精简Last Stage

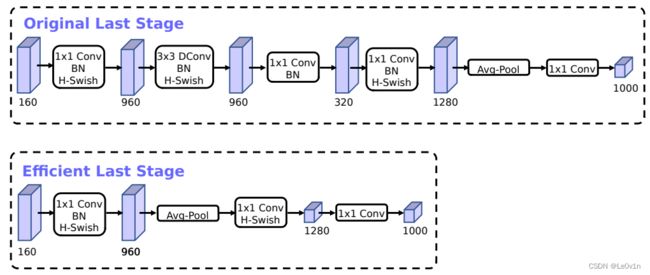
图5. 原始最后阶段和高效最后阶段的比较。这个更有效的最后阶段能够在不损失精度的情况下，在网络的末端放弃三个昂贵的层。

对于原始的Last Stage，它是由1×1 PWConv -> 3×3 DWConv -> 1×1 PWConv -> 1×1 PWConv -> AvgPool -> 1×1 PWConv -> NC

作者发现这个原始的Last Stage是一个比较耗时的部分，于是作者针对该结构进行了精简，即提出了Efficient Last Stage：
1×1 PWConv -> AvgPool -> 1×1 PWConv -> 1×1 PWConv -> NC

和上面的原始Last Stage相比明显少了很多层结构。这么调整之后作者发现在准确率上是没有任何变化的，但节省了7ms的执行时间。

别小看这7ms，它占据了总推理时间的11%。

一旦这个特征生成层的成本得到缓解，就不再需要之前的瓶颈投影层来减少计算量。这个观察结果使我们可以删除前一个瓶颈层中的投影和过滤层，进一步降低计算复杂性。原始和优化的最后阶段可以在图5中看到。高效的最后阶段减少了7毫秒的延迟，占运行时间的11%，并减少了3000万MAdds的操作数，几乎没有精度损失。第6节包含详细的结果。

3.5 重新设计激活函数

3.5.1 h-sigmoid激活函数

在MobileNet v2中使用的激活函数是ReLU6激活函数，该函数的上限为6。借鉴这种思想，h-sigmoid激活函数也有一个上限，其表达式为：

$$\text{h-sigmoid}=\frac{\text{ReLU6}(x+3)}{6}$$

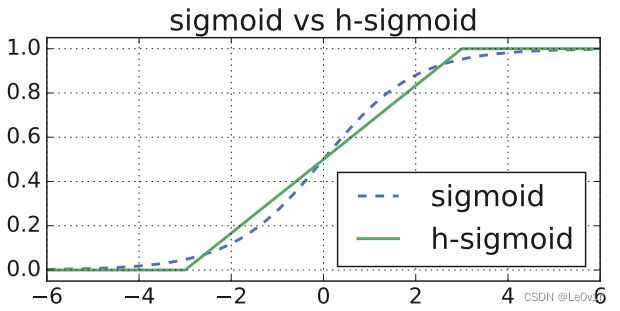
我们看一下sigmoid和h-sigmoid的函数图像：

可以看到，h-sigmoid有了上下线，同时曲线也不再复杂，相比原版的sigmoid来说，计算和求导也更加方便了。

3.5.2 h-swish激活函数

在MobileNet v2中使用的激活函数是ReLU6激活函数。现在比较常用的一个激活函数是swish激活函数，它的计算公式为：

$$\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{h}(x)=x\cdot \sigma (x)$$

其中$\sigma (\cdot )$为Sigmoid激活函数，其计算公式$\sigma (x)=\frac{1}{1+e^{-x}}$。

使用swish激活函数确实可以提高网络的准确率，但它有一些问题：

1. swish激活函数的计算和求导比较复杂（Sigmoid激活函数本身就不利于求导计算）
2. 对量化过程非常不友好，特别是对移动端的设备，为了实现神经网络加速一般都会对网络进行量化处理，但是swish激活函数对量化不友好。

由于存在上面的两个问题，作者就提出了h-swish激活函数，其表达式如下：

$$\begin{array}{rl}\mathrm{h}-\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{h}& =x\cdot \text{h-sigmoid}\\ & =x\cdot \frac{\text{ReLU6}(x+3)}{6}\end{array}$$

我们看一下swish和h-swish激活函数的图像：

可以看到，h-swish和swish是非常相似的，因此使用h-swish代替swish是非常好的。

在原论文中，作者将swish激活函数替换为h-swish激活函数，将sigmoid替换为h-sigmoid，这样可以加速网络的前向推理速度；对模型的量化过程非常友好。

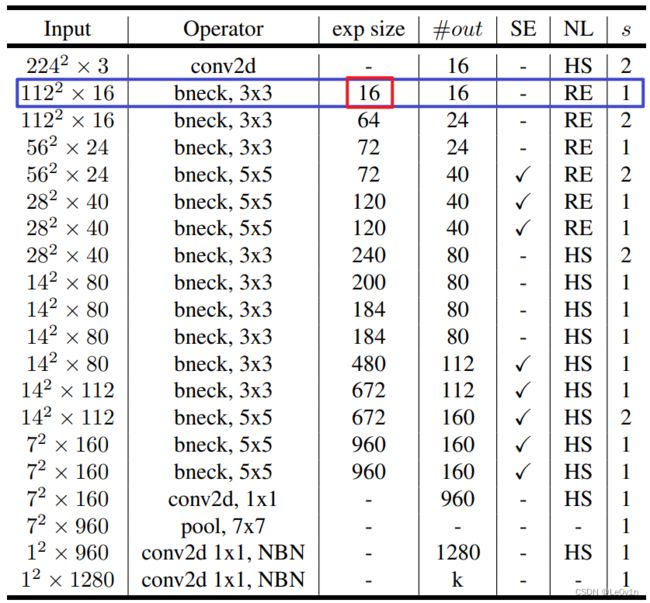
3.6 MobileNet v3-Large 网络架构

其中：

• Input：当前层的输入特征图shape
• Operator：每一层的操作
• exp size：beneck中升维卷积将通道升到exp size倍
• #out：该层输出特征图的channel
• SE：是否使用注意力机制
• NL：使用的是什么激活函数，有H-swish（HS）和ReLU（RE）
• s：Bneck是否会对特征图进行下采样
• NBN：不使用BN层
• k：NC

注意：

• 第一个Bneck的输入channel是16，输出channel也是16（所以这个Bneck中第一个1×1卷积去掉了 ，直接就是DWConv -> BN -> NL -> 1×1 Conv -> BN -> NL；同时也没有SE和shortcut）
• 最后两个conv2d 1×1, NBN其实就是两个FC层，所以不使用BN层

参考

1. https://www.bilibili.com/video/BV1yE411p7L7?spm_id_from=333.999.0.0
2. https://www.bilibili.com/video/BV1GK4y1p7uE/?spm_id_from=333.788