Java学习(Day 28)
学习来源:日撸 Java 三百行(51-60天,kNN 与 NB)_闵帆的博客-CSDN博客
文章目录
- kMeans 聚类
-
- 一、聚类
- 二、kMeans步骤
- 三、代码分析
-
- 1. 流程
- 2. 完整代码
- 3. 运行截图
- 总结
kMeans 聚类
一、聚类
监督式学习: 训练集有明确答案, 监督学习就是寻找问题 (又称输入、特征、自变量) 与答案 (又称输出、目标、因变量) 之间关系的学习方式. 监督学习模型有两类, 分类和回归.
-
分类模型: 目标变量是离散的分类型变量
-
回归模型: 目标变量是连续性数值型变量
无监督式学习: 只有数据, 无明确答案, 即训练集没有标签. 常见的无监督学习算法有聚类 (clustering), 由计算机自己找出规律, 把有相似属性的样本放在一组, 每个组也称为簇 (cluster). 接下来要谈到的 KMeans 就是其中之一.
二、kMeans步骤
K-Means 聚类步骤是一个循环迭代的算法, 非常简单易懂:
-
假定我们要对 N 个样本观测做聚类, 要求聚为 K 类, 首先选择 K 个点作为初始中心点
-
接下来, 按照距离初始中心点最小的原则, 把所有观测分到各中心点所在的类中
-
每类中有若干个观测, 计算 K 个类中所有样本点的均值, 作为第二次迭代的 K 个中心点
-
然后根据这个中心重复第2、3步,直到收敛 (中心点不再改变或达到指定的迭代次数), 聚类过程结束
三、代码分析
1. 流程
Step 1: 从特定文件 iris.arff 读入数据存放在一个特定的数据结构中, 我将它命名为 dataset.
Step 2: 人为地为最后要分的类个数做出规定, 我们这里把类别固定为3, 当然这一操作就感觉是一种上帝视角了.
Step 3: 开始聚类
Step 3.1: 获得一个混淆后的整数数组, 其中存放的是下标, 这个下标指的是数据在 dataset 里的下标.
Step 3.2: 用欧式距离找到各点到中心点距离, 然后把它归到最近的那个类中.
Step 3.3: 重新找中心点, 就是将每个类中所有数据各类别加起来取平均值. 重复 Step 3的步骤直到中心点不变.
2. 完整代码
package kmeans;
import java.io.FileReader;
import java.util.Arrays;
import java.util.Random;
import weka.core.Instances;
/**
* kMeans clustering.
*
* @author Shihuai Wen Email: [email protected].
*/
public class KMeans {
/**
* Manhattan distance.
*/
public static final int MANHATTAN = 0;
/**
* Euclidean distance.
*/
public static final int EUCLIDEAN = 1;
/**
* The distance measure.
*/
public int distanceMeasure = EUCLIDEAN;
/**
* A random instance;
*/
public static final Random random = new Random();
/**
* The data.
*/
Instances dataset;
/**
* The number of clusters.
*/
int numClusters = 2;
/**
* The clusters.
*/
int[][] clusters;
/**
* ******************************
* The first constructor.
*
* @param paraFilename The data filename.
* ******************************
*/
public KMeans(String paraFilename) {
dataset = null;
try {
FileReader fileReader = new FileReader(paraFilename);
dataset = new Instances(fileReader);
fileReader.close();
} catch (Exception ee) {
System.out.println("Cannot read the file: " + paraFilename + "\r\n" + ee);
System.exit(0);
} // Of try
}// Of the first constructor
/**
* ******************************
* A setter.
* ******************************
*/
public void setNumClusters(int paraNumClusters) {
numClusters = paraNumClusters;
}// Of the setter
/**
* ********************
* Get a random indices for data randomization.
*
* @param paraLength The length of the sequence.
* @return An array of indices, e.g., {4, 3, 1, 5, 0, 2} with length 6.
* ********************
*/
public static int[] getRandomIndices(int paraLength) {
int[] resultIndices = new int[paraLength];
// Step 1. Initialize.
for (int i = 0; i < paraLength; i++) {
resultIndices[i] = i;
} // Of for i
// Step 2. Randomly swap.
int tempFirst, tempSecond, tempValue;
for (int i = 0; i < paraLength; i++) {
// Generate two random indices.
tempFirst = random.nextInt(paraLength);
tempSecond = random.nextInt(paraLength);
// Swap.
tempValue = resultIndices[tempFirst];
resultIndices[tempFirst] = resultIndices[tempSecond];
resultIndices[tempSecond] = tempValue;
} // Of for i
return resultIndices;
}// Of getRandomIndices
/**
* ********************
* The distance between two instances.
*
* @param paraI The index of the first instance.
* @param paraArray The array representing a point in the space.
* @return The distance.
* ********************
*/
public double distance(int paraI, double[] paraArray) {
int resultDistance = 0;
double tempDifference;
switch (distanceMeasure) {
case MANHATTAN:
for (int i = 0; i < dataset.numAttributes() - 1; i++) {
tempDifference = dataset.instance(paraI).value(i) - paraArray[i];
if (tempDifference < 0) {
resultDistance -= tempDifference;
} else {
resultDistance += tempDifference;
} // Of if
} // Of for i
break;
case EUCLIDEAN:
for (int i = 0; i < dataset.numAttributes() - 1; i++) {
tempDifference = dataset.instance(paraI).value(i) - paraArray[i];
resultDistance += tempDifference * tempDifference;
} // Of for i
break;
default:
System.out.println("Unsupported distance measure: " + distanceMeasure);
}// Of switch
return resultDistance;
}// Of distance
/**
* ******************************
* Clustering.
* ******************************
*/
public void clustering() {
int[] tempOldClusterArray = new int[dataset.numInstances()];
tempOldClusterArray[0] = -1;
int[] tempClusterArray = new int[dataset.numInstances()];
Arrays.fill(tempClusterArray, 0);
double[][] tempCenters = new double[numClusters][dataset.numAttributes() - 1];
// Step 1. Initialize centers.
int[] tempRandomOrders = getRandomIndices(dataset.numInstances());
for (int i = 0; i < numClusters; i++) {
for (int j = 0; j < tempCenters[0].length; j++) {
tempCenters[i][j] = dataset.instance(tempRandomOrders[i]).value(j);
} // Of for j
} // Of for i
int[] tempClusterLengths = null;
while (!Arrays.equals(tempOldClusterArray, tempClusterArray)) {
System.out.println("New loop ...");
tempOldClusterArray = tempClusterArray;
tempClusterArray = new int[dataset.numInstances()];
// Step 2.1 Minimization. Assign cluster to each instance.
int tempNearestCenter;
double tempNearestDistance;
double tempDistance;
for (int i = 0; i < dataset.numInstances(); i++) {
tempNearestCenter = -1;
tempNearestDistance = Double.MAX_VALUE;
for (int j = 0; j < numClusters; j++) {
tempDistance = distance(i, tempCenters[j]);
if (tempNearestDistance > tempDistance) {
tempNearestDistance = tempDistance;
tempNearestCenter = j;
} // Of if
} // Of for j
tempClusterArray[i] = tempNearestCenter;
} // Of for i
// Step 2.2 Mean. Find new centers.
tempClusterLengths = new int[numClusters];
Arrays.fill(tempClusterLengths, 0);
double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
// Arrays.fill(tempNewCenters, 0);
for (int i = 0; i < dataset.numInstances(); i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[tempClusterArray[i]][j] += dataset.instance(i).value(j);
} // Of for j
tempClusterLengths[tempClusterArray[i]]++;
} // Of for i
// Step 2.3 Now average
for (int i = 0; i < tempNewCenters.length; i++) {
for (int j = 0; j < tempNewCenters[0].length; j++) {
tempNewCenters[i][j] /= tempClusterLengths[i];
} // Of for j
} // Of for i
System.out.println("Now the new centers are: " + Arrays.deepToString(tempNewCenters));
tempCenters = tempNewCenters;
} // Of while
// Step 3. Form clusters.
clusters = new int[numClusters][];
int[] tempCounters = new int[numClusters];
for (int i = 0; i < numClusters; i++) {
if (tempClusterLengths != null) {
clusters[i] = new int[tempClusterLengths[i]];
}
} // Of for i
for (int i = 0; i < tempClusterArray.length; i++) {
clusters[tempClusterArray[i]][tempCounters[tempClusterArray[i]]] = i;
tempCounters[tempClusterArray[i]]++;
} // Of for i
System.out.println("The clusters are: \r\n");
for (int i = 0; i < clusters.length; i++) {
System.out.print("clusters " + i + ": ");
for (int j = 0; j < clusters[i].length; j++) {
System.out.print( clusters[i][j] + " ");
}
System.out.println();
}
}// Of clustering
/**
* ******************************
* Clustering.
* ******************************
*/
public static void testClustering() {
KMeans tempKMeans = new KMeans("D:/Work/sampledata/iris.arff");
tempKMeans.setNumClusters(3);
tempKMeans.clustering();
}// Of testClustering
/**
* ************************
* A testing method.
* ************************
*/
public static void main(String[] args) {
testClustering();
}// Of main
} // Of class KMeans
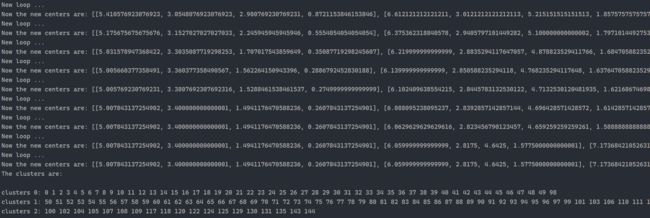
3. 运行截图
总结
kMeans 优点在于原理简单, 容易实现, 聚类效果好.
当然, 也有一些缺点:
-
K 值、初始点的选取不好确定.
-
得到的结果只是局部最优.
-
受离群值影响大.