Java学习(Day 36)
学习来源:日撸 Java 三百行(81-90天,CNN 卷积神经网络)_闵帆的博客-CSDN博客
文章目录
- 前言
- 卷积神经网络 (理论篇)
-
- 一、卷积核
- 二、卷积运算
- 三、非线性激活层
- 四、池化层
- 五、全连接层
- 六、训练和优化
- 总结
前言
本文大多内容来自 知乎文章: 卷积神经网络CNN完全指南终极版(一)
我将借用文章中的图片用自己的方式去理解 CNN.
图片最初来源是 YouTube 上一位博主的视频截图. B 站有视频转载【CNN】Youtube上迄今为止最好的卷积神经网络入门教程
卷积神经网络 (理论篇)
一、卷积核
卷积神经网络在现在已经被应用于各个领域, 尤其是图像识别这个方面. 但 CNN 真正能做的, 只是起到一个特征提取器的作用. 所以诸多看似不同领域的应用, 都是建立在 CNN 对图像进行特征提取的基础上进行的.
说到特征提取, 可能有点抽象. 简单举个例子, 比如我现在拿到一堆动物园里面动物的照片, 这时我想找到长颈鹿, 我就会去看哪张照片里面哪个动物有长颈这个特征.
这算是主观上的特征提取, 但在计算机中就不太会这样做. 因为计算机哪知道什么叫长颈, 说不定还会把东方明珠塔也看做长颈鹿. 如何避免这种情况以后再议, 不过现在总算对特征提取有些感触了.
那么现在有一张图片如下所示
我们要让计算机知道这张图片是 ‘X’ 还是 ‘O’. 当然不仅仅是这一种 ‘X’, 还有一些奇奇怪怪的 ‘X’ 也需要被识别出来.
计算机中对图片的存储是以像素值的方式来存储的, 本文中的图片都是黑白图片, 那么对应的像素值就只有两种. 那么就可以用值 1 表示白色像素点, 值 -1 表示黑色像素点. 当然用值 0 1 来表示也可以. 要是彩色图片就要转为灰度图, 要是色彩是 RGB, 灰度值就是在 (0, 255) 中的某个整数.
假设上面两张图分别是训练集和测试集, 最简单的方式就是逐一对比之间的像素点, 那么这样虽然可以说是识别字符, 实际上却是判断两张图片在磁盘中存储内容是否一致了. 这种方式是首先被排除的.
然后我们观察到两张图中实际是有一部分相似的, 可以把这部分叫做特征.
在图中三个同色区域的结构完全一致. 所以我们就从全局像素点的匹配转化为了局部像素点的匹配. 那么这个局部像素点就有之前所提到的特征提取那味道了.
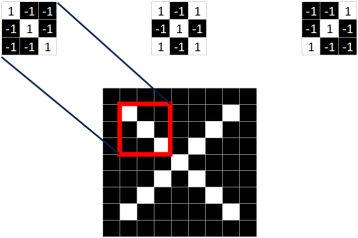
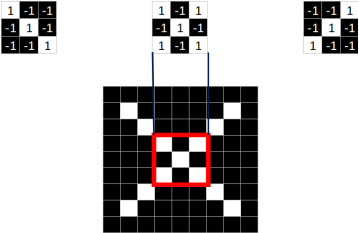
那么我们从图中找出几个特征.
这样就能通过这些特征定位到图片的某个局部图像. 那么这些特征在 CNN 中也被称为卷积核.
二、卷积运算
卷积就是卷起来的乘积, 可以理解为累加或叠加 (对连续函数为积分) 起来的乘积.
连续形式:
f ( x ) ∗ g ( x ) = ∫ − ∞ ∞ f ( τ ) × g ( x − τ ) d τ (1) f(x) * g(x) = \int_{-\infty}^{\infty}f(\tau) \times g(x - \tau) d\tau \tag{1} f(x)∗g(x)=∫−∞∞f(τ)×g(x−τ)dτ(1)
离散形式:
f [ n ] ∗ g [ n ] = ∑ m = − ∞ ∞ f [ m ] × g [ n − m ] (2) f[n] * g[n] = \sum_{m=-\infty}^{\infty} f[m] \times g[n-m] \tag{2} f[n]∗g[n]=m=−∞∑∞f[m]×g[n−m](2)
不必太过在意这些公式, 只需要记住卷积的本质是过滤信息然后得到我们想要的那部分. 接下来才是重中之重, 怎么算?
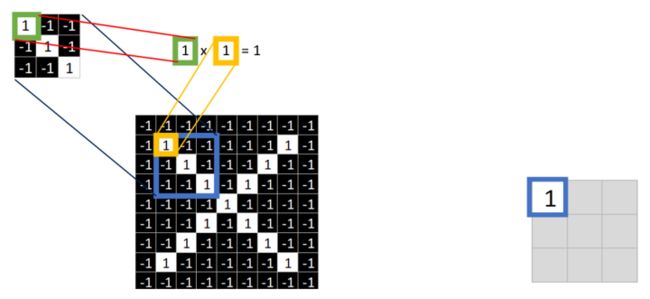
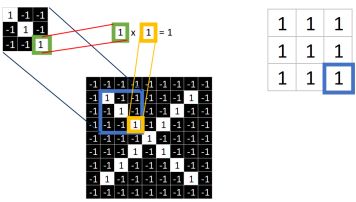
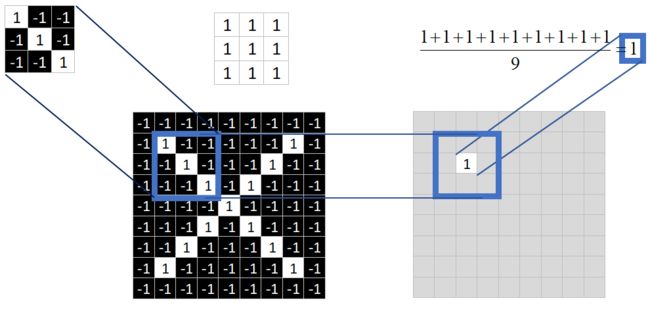
取一个特征, 再在目标图像中找一个和特征同样大小的像素值集合, 二者相同位置的相乘, 最后在矩形方框中这个位置填入相乘的值. 具体过程如下图所示.
当计算完成后就会得到下图中右侧的矩形方框.
接下来就是对得到的矩形方框中九个值求平均, 得到的均值将作为新图像中一个像素点.
新图像只有一个像素点怎么可以呢, 这时考虑到图片中蓝色方框的位置, 要是有不同位置的蓝色方框那么通过卷积运算不就有多个像素点了. 正是由于这种想法, 我们就把这个蓝色方框叫做窗口.
窗口的起始位置是在图像的左上角
当进行完当前的运算后, 窗口就会发生移动. 涉及移动, 自然就要考虑移动的方向和快慢, 方向先是自左向右, 再是自上向下, 快慢程度叫做步长.
比如若步长为 1, 就往右边移动一个像素点, 当不能右移时就回到最左边并向下移动一个像素点.
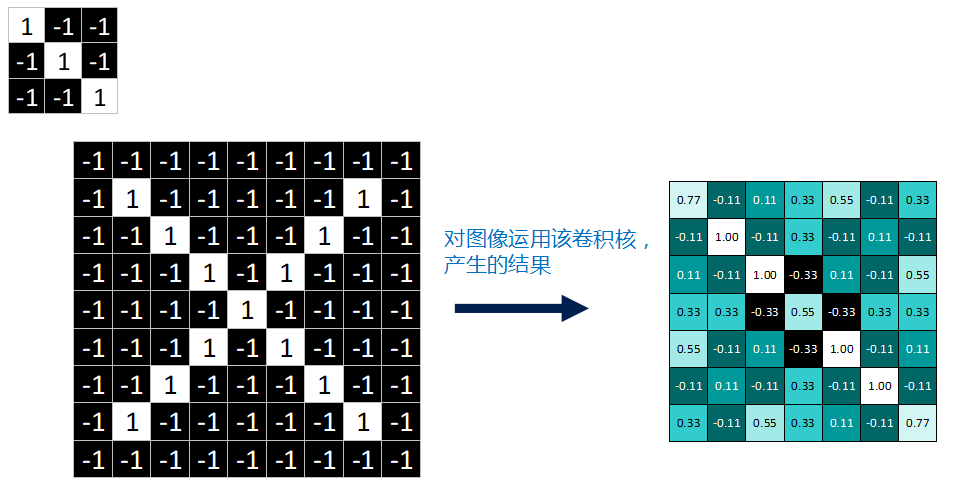
当我们对整个图像进行处理后就会得到这样一个图像.
其中的值, 越接近为 1 表示对应位置和特征的匹配越完整, 越是接近 -1, 表示对应位置和特征的反面匹配越完整, 而值接近 0 的表示对应位置没有任何匹配或者说没有什么关联.
三、非线性激活层
在神经网络中用到最多的非线性激活函数是 Relu 函数, 它的公式定义如下:
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
这个函数的输出是, 保留大于等于 0 的值, 其余所有小于 0 的数值直接改写为 0.
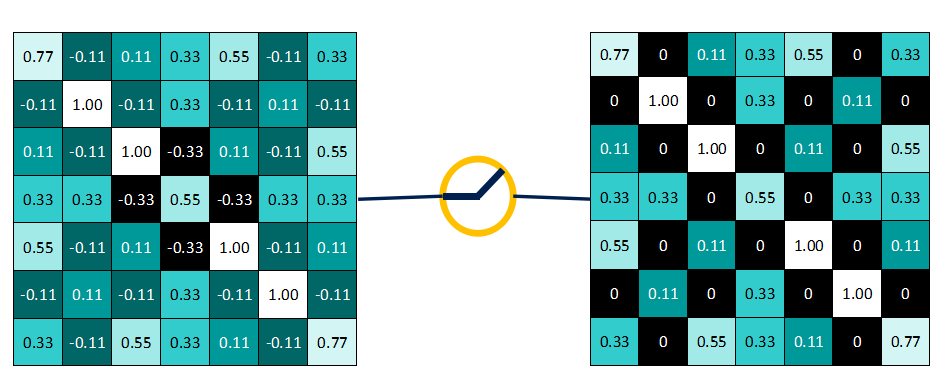
为什么要这么做呢? 上面说到, 卷积后产生的特征图中的值, 越靠近 1 表示与该特征越关联, 越靠近 -1 表示越不关联, 而我们进行特征提取时, 为了使得数据更少, 操作更方便, 就直接舍弃掉那些不相关联的数据.
那么之前通过卷积运算得到的图像进行处理后就会得到以下图像.
四、池化层
卷积操作后, 我们得到了一张张有着不同值的特征图, 尽管数据量比原图少了很多, 但还是过于庞大 (比较深度学习动不动就几十万张训练图片), 因此接下来的池化操作就可以发挥作用了, 它最大的目标就是减少数据量.
池化分为两种, Max Pooling 最大池化、Average Pooling 平均池化. 顾名思义, 最大池化就是取最大值, 平均池化就是取平均值.
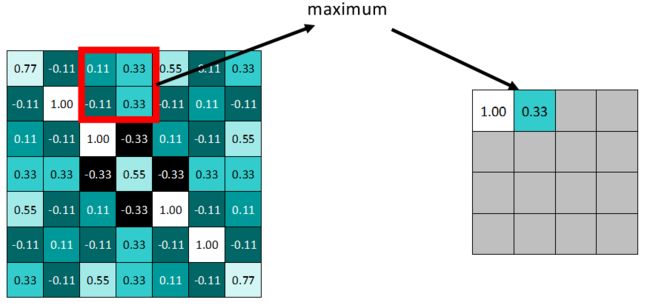
拿最大池化举例:选择池化尺寸为 2x2, 因为选定一个 2x2 的窗口, 在其内选出最大值更新进新的特征图.
窗口滑动和之前做卷积运算时一样, 这里设置步长为 2.
在做完所有操作后就能得到一个新的特征图.
很明显地可以发现相比起之前的图缩小了很大一部分.
因为最大池化保留了每一个小块内的最大值, 所以它相当于保留了这一块最佳匹配结果 (因为值越接近1表示匹配越好). 这也就意味着它不会具体关注窗口内到底是哪一个地方匹配了, 而只关注是不是有某个地方匹配上了. 这也就能够看出, CNN 能够发现图像中是否具有某种特征, 而不用在意到底在哪里具有这种特征. 这也就能够帮助解决之前提到的计算机逐一像素匹配的死板做法.
五、全连接层
在之前了解了 CNN 的卷积层、池化层和激活层. 整个处理流程如下图所示.
我们通过三个不同的卷积核得到了不同的三个特征图.
但是光凭这些还是不能识别出图片中的字符是什么, 这就需要提到 CNN 的两个精髓, 局部连接和参数共享.
说局部连接前先说全连接, 之前所学的 BP 神经网络就是全连接, 这一层的每一个节点都会指向下一层的同一个节点. 下一层有多少个节点就会进行这样的操作多少次. 例如, 输入层有 10 个节点, 隐藏层有 3 个节点, 那么两层之间就应该有 10 × 3 10 \times 3 10×3 条代表权值的线.
反观 CNN 要是采用全连接就是要对每一个像素点建立一个节点, 而不是人为制造一个窗口. 这样的形式就是局部连接, 层与层之间联系的最小单位就是窗口的大小. 参数共享就是指窗口滑动的过程.
之前一直在说识别图像, 其实这个表达存在问题. 因为字符是有限的, 所以我们解决的问题其实是分类问题. 正如我们发现了外星人的语言文字, 我们不能准确用外星语言说出来, 但是我们可以说这个像字母表中的某个字母.
我们对结果进行统计分析后可判断这张图片里的字母为 X. 这里的统计分析实际上是对所得到的特征表进行一个整合, 在之前这些特征表相当于图中的碎片, 在这一步我们就是要把碎片拼接起来形成一个值. 这个值的大小就代表了图片中的字符属于哪个类别.
得到这个值归根结底是需要一个激活函数, 像之前提到的 S i g m o i d Sigmoid Sigmoid 函数就可以完成这个工作. 或者采用 S o f t m a x Softmax Softmax 函数.
六、训练和优化
可以看出整个算法的关键在于卷积核, 有几个卷积核就表示需要提取到几个特征表.
在全文中对于卷积核采用的是直接取得原始图像中的一部分, 这样是有失偏颇的. 因为我们对图像的认识有了一个直觉性的判断, 在实际训练中采用的还是对卷积核随机化.
和矩阵分解以及 BP 神经网络一样, CNN 采用的也是随机那个关键性的数据. 那么要使得模型的准确性高, 和之前学过的算法一样也要采用梯度下降的方式.
具体内容就在代码篇进行详细的解释.
总结
开始写文章的时候, 总觉得 CNN 对图像的处理是将图像进行 “马赛克” 化, 就像图片压缩算法那样, 将一个像素点的颜色延伸到周围, 最后就感觉图像就成为了一个又一个的小方块集合, 但是我们还是能辨认出图像表达的意思.
写完文章后发现, CNN 其实更像是在 “拼拼图”. 例如我们要拼一只猫, 我们会找它的眼睛、耳朵和尾巴等具有代表性的东西, 这些东西在算法中就是得到的特征图, 但是怎么区别眼睛、耳朵和尾巴呢?和拼猫一样, 总有小的碎片能够拼成眼睛、耳朵和尾巴, 这些就类似算法上一层的到的特征图.
“马赛克” 的思想是从整体到局部, 可能有效但不能被计算机采纳. 而 “拼拼图” 的思想是从局部到整体, 将混乱整理为有序.