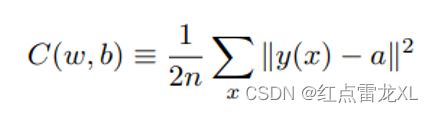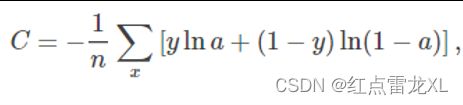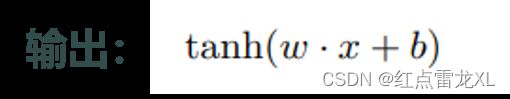【neural networks and deep learning学习笔记】chapter3 改进神经网络的学习方法
在上一章的内容中,学到了反向传播算法的工作方法,其中主要学习到了反向传播算法的目的和思路。反向传播算法的原理方面是基于对代价函数的两个假设和四个基本方程,最终使得我们能够高效的对网络的代价函数的偏导进行计算。
那么本章中,首先举出了一个使用二次代价函数在网络数字分类方面的弊端,也就是学习缓慢的问题,还有后面学习到的一些用于改善神经网络的技巧方法。
- 交叉熵函数
- 交叉熵函数代码
- softmax层
- 过度拟合和规范化
- 权重初始化
- 选择网络的超参数
- 人工神经元的其他模型
二次代价函数出现的问题
首先书中给出了一个实验,既:
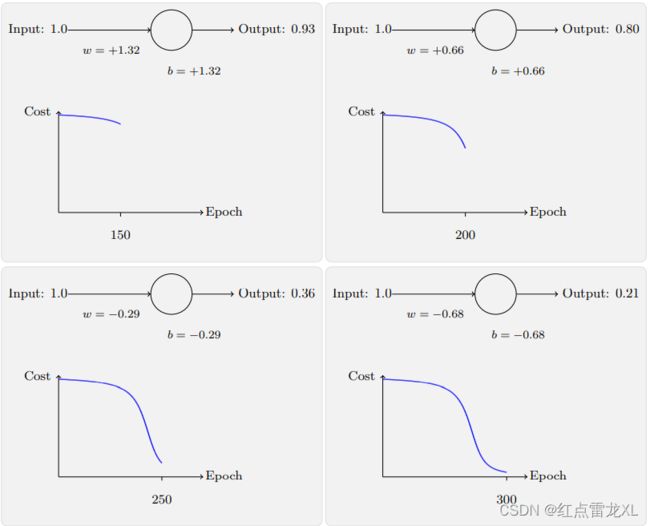
给出一个只有一个输入的神经元,然后对这个神经元进行训练,训练内容也是简单的:让输入1转化为0。当然看起来这个训练的权重和偏置是特别简单的,不急,让我们使用二次代价函数进行梯度下降的方式进行学习权重和偏置。
然后观察神经元的学习情况。
其中书中给出了很多,其中我们可以看到,一开始代价函数下降的速率是相当缓慢的。
那,为什么缓慢呢,从函数的方面验证这一现象:
当我们使用了上面给出的神经元后,二次代价函数就可以精简一下了
然后对其进行求导我们可以得到神经元的偏导值:
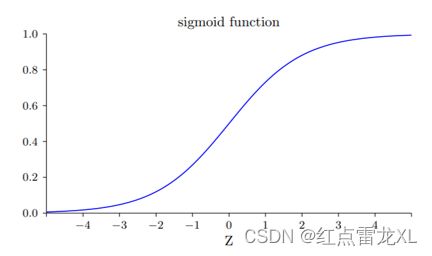
从公式中我们可以看出,二次代价函数的偏导值与sigmoid函数的导数值是相关的,再回头看一下sigmoid函数的图像。
从中我们不难看出,当sigmoid函数的输出值接近0或者1时,函数的导数值是非常小的,在图像上表现为斜率。根据这个我们就可以解释这个神经元开始时学习缓慢的因素了。因为一开始我们使用的权重和偏置都是随机设置或者都是统一为0的值,此时输入时容易使sigmoid函数处于导数很小的位置。
sigmoid函数的导数值很低的情况下,二次代价函数的偏导数值也就会很低,C的变化量也就变低,我想这就是一开始时cost下降缓慢的原因了。
那么有什么解决办法呢?书中引入了交叉熵代价函数。
交叉熵代价函数
其中神经元的输出就是 a = σ(z),其中z是输入的带权和。 n 是训练数据的总数,求和是在所有的训练输⼊ x 上进行的,y 是对应的⽬标输出。
然后再用同样的方法进行对交叉熵代价函数的输出值计算。
其中我只对相应的权重进行了偏导数的计算,我想对于偏置来说计算方法也是一样的。
其中我们对于sigmoid函数的导数值也加以利用,最终抵消掉了sigmoid函数的导数值,剩下了函数值。这也就表明了我们代价函数的偏导数不再依赖于sigmoid函数的导数值。
从书中实验结果来看无疑是取得了成功的。成功的解决了二次代价函数的开始学习缓慢问题。
交叉熵代价函数代码
从书中给出的实验中我们也能找到相应的使用交叉熵代价函数的代码。
所在位置在network2.py中
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
"""Return the cost associated with an output ``a`` and desired output
``y``. Note that np.nan_to_num is used to ensure numerical
stability. In particular, if both ``a`` and ``y`` have a 1.0
in the same slot, then the expression (1-y)*np.log(1-a)
returns nan. The np.nan_to_num ensures that that is converted
to the correct value (0.0).
"""
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
"""Return the error delta from the output layer. Note that the
parameter ``z`` is not used by the method. It is included in
the method's parameters in order to make the interface
consistent with the delta method for other cost classes.
"""
return (a-y)
其中的我们能够找到如图所示的二次代价函数的具体公式。
SoftMax层
除了使用交叉熵函数代替二次代价函数可以解决学习缓慢的问题,书中提到还可以通过增加一个softmax层的神经元来解决这个问题。
通常情况输出层使用sigmoid函数作为激活函数,而再softmax层的激活函数为:
在分母,对softmax层的所有神经元求和。可以看到,输出相当于在求一个加权的权重,对于整体数据也就是一个概率分布,当然此处求权重的方法是通过指数函数。输出层的所有输出就可以看是是一个概率分布了,加起来概率为1。
过度拟合和规范化
解决完学习缓慢的问题后,在书中实验内还容易出现的一种问题就是关于过度拟合的问题,此类问题主要是在得到一个好的结果(比如分类准确率)后,无法及时的停止训练,导致浪费时间在无用功上。
比如通过分类准确率体现过度拟合的状态:
其中我们可以看到,在100eopch后分类的准确率以及很高了,而且几乎提升很小,所以我们是在用大量的时间获得很小的提升,这种是不划算的,或者说是浪费的。
过度拟合是神经网络的⼀个主要问题。这在现代⽹络中特别正常,因为网络权重 和偏置数量巨大。为了高效地训练,我们需要⼀种检测过度拟合是不是发⽣的技术,这样我们不会过度训练。
关于过拟合的概念,学习的过程中理解为在训练数据上拟合过度了,而这个时候训练数据上的代价比较小。
其中学习了几种解决过度拟合的方法:
其中的弃权更像是通过分组来训练不同的神经网络,不同的网络会以不同的方式过度拟合,所以弃权过的网络,在效果上会减轻过度拟合。
此外还有扩充训练集的方法,比如人为的扩展数据集,通过旋转15°等等。
权重初始化
之前我们的权重的偏置的初始化都是像第一章中那样被随机初始化。而现在我们根据独立高斯随机变量来选择权重和偏置,其被归⼀化为均值为 0,标准差 1。
假设我们有⼀个有 n_in 个输⼊权重的神经元。我们会使⽤均值为 0 标准差为 1/ sqrt(n_in) 的高斯随机分布初始化这些权重。也就是说,我们会向下挤压高斯分布,让我们的神经元更不可能饱和。这样就可以使隐藏层神经元的输入为一个标准正态分布的随机变量了。
选择网络的超参数
书中也提到了一些选择超参数的方法,比如选择网络的学习速率![]() 或者是梯度下降时的小批量数据大小m。下面就是一些策略。
或者是梯度下降时的小批量数据大小m。下面就是一些策略。
宽泛策略:选择减少训练的样本和网络的复杂度,以达到调整修改超参数的目的。
使用提前停止来确定训练的迭代期数量:计算验证集上的分类准确率,当准确率不再提升,就终止它。
自动技术:是网格搜索(grid search),可以系统化地对超参数的参数空间的网格进行搜索。
人工神经元的其他模型
书中还接触到了一些其他的人工神经元。
双曲正切神经元
其中hanh函数的定义是:
修正线性神经元(ReLU)
relu函数的图像:
其中这个relu函数我是使用过的,曾经我的毕业设计中使用的就是这个神经元。
上述就是我在第三章接触到的主要内容了。下一章就是第六章了,我打算直接写一下我的实验过程。当然还有一小部分新接触的概念等等。
此外做到这里还有些想回忆的:
其中的relu函数曾经使用过的,当时做的也是一个图像识别的项目(我的毕设),不过分为两步,第一步的CTPN将图中的文字圈出来一开始就是使用了这个神经元,当时还是觉得挺困难的把哈哈,当然现在看来也没有那么困难了,毕竟本质上也是一个二分类的问题。
具体一点的话就是分为16个类型的框框,16种的话是指16种高度,宽度的话都是一样的,然后在图像上预设很多个这样的框框(称为anchor),然后对这些anchor进行二分类操作,最终分类为true(也就是有字)的anchor进行整合,进行一个anchor合并的一个操作。然后就可以得到有字的位置了,当然做完后显示的话是不显示anchor的只会整个的一个有图像的区域了。不过也能让他的分类为true的anchor显示出来。
我想我应该会把毕设写一写的把,嗯,应该会吧。。
(回想起被毕设折磨的痛苦)@.@
文章参考书:Neural networks and deep learning