【机器学习】-第8章-聚类算法
文章目录
- 8-聚类算法
-
- 8.1 聚类任务
-
- 8.1.1 概念
- 8.1.2 问题描述
- 8.1.3 算法分类
- 8.1.4 数学准备
-
- 1) 类或簇
- 2) 类或簇的特征
- 3) 类与类之间的距离
- 8.2 评价指标
-
- 8.2.1 外部指标
-
- 1) Jaccard系数
- 2) FM指数
- 3) Ran指数
- 4) Mirkin指数
- 8.2.2 内部指标
-
- DB指数
- Dunn指数
- 8.3 距离计算(相似度)
-
- 1) 性质
- 2) 闵可夫斯基距离
- 3) 马哈拉诺比斯距离
- 4) 相关系数
- 5) 夹角余弦
- 8.4 原型聚类(划分式聚类)
-
- 8.4.1 K均值(k-means)
-
- 1) 概念
- 2) 算法推导
- 3) 例子
- 4) 优缺点
- 8.4.2 LVQ
- 8.4.3 高斯混合聚类GMM
-
- 1) 介绍
- 2) 数学准备
-
- a) 高斯分布
- b) 多元高斯分布
- c) 贝叶斯公式
- d) 极大似然
- 2) 算法推导
- 3) 例子
- 8.5 密度聚类
-
- 8.5.1 概念
- 8.5.2 相关概念
- 8.5.3 DBSCAN算法推导
- 8.5.4 代码
- 8.5.5 优缺点
- 8.6 层次聚类
-
- 8.6.1 概念
- 8.6.2 数学准备
- 8.6.3 算法推导
- 8.6.4 例子
8-聚类算法
文章链接:https://gitee.com/fakerlove/machine-learning
8.1 聚类任务
什么是聚类,聚类是做什么的
8.1.1 概念
机器学习里面的聚类是无监督的学习问题,它的目标是为了感知样本间的相似度进行类别归纳。它可以用于潜在类别的预测以及数据压缩上去。
潜在类别预测,比如说可以基于通过某些常听的音乐而将用户进行不同的分类。数据压缩则是指将样本进行归类后,就可以用比较少的的One-hot向量来代替原来的特别长的向量。
聚类,既可以作为一个单独的过程,也可以作为其他机器学习任务的预处理模块。
8.1.2 问题描述
给定一个包含 N N N个样本的样本集 X = { x 1 , x 2 , . . . , x N } X=\{x_1,x_2,...,x_N\} X={x1,x2,...,xN},要给对这N个样本给定一个划分方式,将这些样本划分为m类 C 1 , C 2 , C 3 , . . . , C m C_1,C_2,C_3,...,C_m C1,C2,C3,...,Cm,使得满足
C i ≠ ϕ , i = 1 , 2 , . . . , m C_i\ne \phi,i=1,2,...,m Ci=ϕ,i=1,2,...,m
U i = 1 , 2 , . . , m C i = X U_{i=1,2,..,m}C_i=X Ui=1,2,..,mCi=X
C i ⋂ C j = ϕ , i ≠ j C_i\bigcap C_j=\phi,i\ne j Ci⋂Cj=ϕ,i=j
8.1.3 算法分类
聚类算法主要有:
- 序贯法
- 层次分析法
- 基于损失函数最优化的:K-means,概率聚类
- 基于密度的聚类
- 其他特殊聚类方法:基因聚类算法,分治限界聚类算法;子空间聚类算法;基于核的聚类方法。
问题的提出
虽然 聚类看起来是很棒的,可以进行“物以类分,人以类聚”,但是聚类确守很多方面的影响。
例如:
1.属性选择不同,导致不同的结果
2.相似度度量不同,导致不同的结果
3.聚类的方法不同,导致不同的结果如何衡量无监督学习的指标
- 性能指标
- 距离计算
8.1.4 数学准备
样本集合中由n个样本,每个样本由m个属性的特征向量组成,样本集合可以用矩阵X表示:
X = [ x i j ] m × n = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋯ ⋮ x m 1 x m 2 ⋯ x m n ] X=[x_{ij}]_{m\times n}=\begin{bmatrix} x_{11}&x_{12}&\cdots&x_{1n} \\ x_{21}&x_{22}&\cdots&x_{2n} \\ \vdots &\vdots&\cdots&\vdots \\ x_{m1}&x_{m2}&\cdots&x_{mn} \end{bmatrix} X=[xij]m×n=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2⋯⋯⋯⋯x1nx2n⋮xmn⎦⎥⎥⎥⎤
给定样本集合X, x i , x j ∈ X , x i = ( x 1 i , x 2 i , . . . , x m i ) T , x j = ( x 1 j , x 2 j , . . . , x m j ) T x_i,x_j\in X,x_i=(x_{1i},x_{2i},...,x_{mi})^T,x_j=(x_{1j},x_{2j},...,x_{mj})^T xi,xj∈X,xi=(x1i,x2i,...,xmi)T,xj=(x1j,x2j,...,xmj)T
1) 类或簇
用 G G G表示类或簇,用 x i , x j x_i,x_j xi,xj表示类中的样本, N G N_G NG表示 G G G中的样本个数, d i j d_{ij} dij表示样本 x i x_i xi与样本 x j x_j xj之间的距离
类或簇的定义
设给定的整数 ,若集合 G G G中的任意两个样本 x i , x j x_i,x_j xi,xj,有 d i j ≤ T d_{ij}\le T dij≤T, 则称 G G G表示为一个类或簇
2) 类或簇的特征
-
类的均值 x ‾ G = 1 N G ∑ i = 1 N G x i \overline{x}_G=\frac{1}{N_G}\sum_{i=1}^{N_G}x_i xG=NG1∑i=1NGxi
-
类的直径 D G = m a x x i , x j ∈ G d i j D_G=max_{x_i,x_j\in G}d_{ij} DG=maxxi,xj∈Gdij
-
类的样本散步矩阵 A G = ∑ i = 1 N G ( x i − x ‾ G ) ( x i − x ‾ G ) T A_G=\sum_{i=1}^{N_G}(x_i-\overline{x}_G)(x_i-\overline{x}_G)^T AG=∑i=1NG(xi−xG)(xi−xG)T
-
样本协方差矩阵
S G = 1 m − 1 A G S_G=\frac{1}{m-1}A_G SG=m−11AG
= 1 m − 1 ∑ i = 1 N G ( x i − x ‾ G ) ( x i − x ‾ G ) T =\frac{1}{m-1}\sum_{i=1}^{N_G}(x_i-\overline{x}_G)(x_i-\overline{x}_G)^T =m−11∑i=1NG(xi−xG)(xi−xG)T
3) 类与类之间的距离
类 C p C_p Cp和类 C q C_q Cq之间的距离 D ( p , q ) D(p,q) D(p,q),也称为连接
前四种方法定义的 C p C_p Cp和 C q C_q Cq之间的距离如下表所示。
| 相似度度量标准(距离大小) | |
|---|---|
| 最短距离或单连接(Single-link) | $D_{pq}=min{d_{ij |
| 最长距离或完全连接(Complete-link) | $D_{pq}=max{d_{ij} |
| 中心距离 | D p q = d x ‾ p x ‾ q D_{pq}=d_{\overline{x}_p\overline{x}_q} Dpq=dxpxq |
| 平均距离(UPGMA) | D p q = 1 C p C q ∑ x i ∈ C p ∑ x j ∈ C q d i j D_{pq}=\frac{1}{C_pC_q}\sum_{x_i \in C_p}\sum_{x_j \in C_q}d_{ij} Dpq=CpCq1∑xi∈Cp∑xj∈Cqdij |
8.2 评价指标
评价聚类算法性能好坏的
聚类性能度量大致分两类,
一类是将聚类结果与某个"参考模型",进行比较,称为外部指标,
另一类是直接参考聚类结果而不利用任何参考模型,称为内部指标
8.2.1 外部指标
a = ∣ S S ∣ , S S = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } b = ∣ S D ∣ , S D = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ ≠ λ j ∗ , i < j } c = ∣ D S ∣ , D S = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ = λ j ∗ , i < j } b = ∣ D D ∣ , D D = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ ≠ λ j ∗ , i < j } a=|SS|,SS=\{(x_i,x_j)|\lambda_i=\lambda_j,\lambda_i^*=\lambda_j^*,i
和混淆矩阵差不多。
其中a表示 C C C中隶属于相同簇且在与 C ∗ C^* C∗也属于相同簇的样本对,
b b b表示 C C C中隶属于相同簇但在与 C ∗ C^* C∗中隶属于不同簇的样本对
| S | D | |
|---|---|---|
| S | |SS| | |SD| |
| D | |DS| | |DD| |
1) Jaccard系数
(Jaccard Coefficient,简称JC)
J C = a a + b + c JC=\frac{a}{a+b+c} JC=a+b+ca
2) FM指数
Fowlkes adn Mallows Index,简称FMI
F M I = a a + b ⋅ a a + c FMI=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}} FMI=a+ba⋅a+ca
3) Ran指数
可知 a + b + c + d = m ( m − 1 ) / 2 a+b+c+d=m(m-1)/2 a+b+c+d=m(m−1)/2
Rand Index,简称RI
m表示样本总数
R = a + d a + b + c + d = 2 ( a + d ) m ( m − 1 ) R=\frac{a+d}{a+b+c+d}=\frac{2(a+d)}{m(m-1)} R=a+b+c+da+d=m(m−1)2(a+d)
4) Mirkin指数
M K = b + c a + b + c + d = 2 ( b + c ) m ( m − 1 ) MK=\frac{b+c}{a+b+c+d}=\frac{2(b+c)}{m(m-1)} MK=a+b+c+db+c=m(m−1)2(b+c)
上诉性能度量的结果均在[0,1]之间,值越大越好
例子
下面,一共有
5个样本,分成2簇。
使用聚类计算的答案
| 类别 | 物体 |
|---|---|
| C 1 C_1 C1 | x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 |
| C 2 C_2 C2 | x 4 , x 5 x_4,x_5 x4,x5 |
目标答案
| 类别 | 物体 |
|---|---|
| C 1 ∗ C_1^* C1∗ | x 1 , x 2 , x 4 x_1,x_2,x_4 x1,x2,x4 |
| C 2 ∗ C_2^* C2∗ | x 3 , x 5 x_3,x_5 x3,x5 |
根据上面计算的和目标答案,做出
a表示 C C C中
隶属于相同簇且在与 C ∗ C^* C∗也属于相同簇的样本对。只有 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)符合这样子的条件。在 C C C中 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)属于 C 1 C_1 C1簇,在 C ∗ C^* C∗中 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)属于 C 1 C_1 C1簇。其他都不满足
| a=|SS| | ( x 1 , x 2 ) (x_1,x_2) (x1,x2) | 1 |
| b=|SD| | ( x 1 , x 3 ) , ( x 2 , x 3 ) , ( x 4 , x 5 ) (x_1,x_3),(x_2,x_3),(x_4,x_5) (x1,x3),(x2,x3),(x4,x5) | 3 |
| c=|DS| | ( x 1 , x 4 ) , ( x 2 , x 4 ) , ( x 3 , x 5 ) (x_1,x_4),(x_2,x_4),(x_3,x_5) (x1,x4),(x2,x4),(x3,x5) | 3 |
| d=|DD| | ( x 1 , x 5 ) , ( x 2 , x 5 ) , ( x 3 , x 4 ) (x_1,x_5),(x_2,x_5),(x_3,x_4) (x1,x5),(x2,x5),(x3,x4) | 3 |
计算的外部指标为
J C = a a + b + c = 1 7 JC=\frac{a}{a+b+c}=\frac{1}{7} JC=a+b+ca=71
F M I = a a + b ⋅ a a + c = 1 4 FMI=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}=\frac{1}{4} FMI=a+ba⋅a+ca=41
R = 2 ( a + d ) m ( m − 1 ) = 2 5 R=\frac{2(a+d)}{m(m-1)}=\frac{2}{5} R=m(m−1)2(a+d)=52
8.2.2 内部指标
考虑聚类结果的簇划分 C = { C 1 , C 2 , ⋯ , C k } C=\{C_1,C_2,\cdots,C_k\} C={C1,C2,⋯,Ck}定义
a v g ( C ) = 2 ∣ C ∣ ( ∣ C ∣ − 1 ) ∑ 1 ≤ i < j ≤ ∣ C ∣ d i s t ( x i , x j ) d i a m ( C ) = max 1 ≤ i < j ≤ ∣ C ∣ d i s t ( x i , x j ) d m i n ( C i , C j ) = min x i ∈ C i , x j ∈ C j d i s t ( x i , x j ) d c e n ( C i , C j ) = d i s t ( μ i , μ j ) avg(C)=\frac{2}{|C|(|C|-1)}\sum_{1\le i
举个例子
avg©–簇内样本的平均距离
a v g ( C 1 ) = 2 3 × ( 3 − 1 ) × ( ∣ x 1 − x 2 ∣ + ∣ x 1 − x 3 ∣ + ∣ x 2 − x 3 ∣ ) a v g ( C 2 ) = 2 2 × ( 2 − 1 ) × ( ∣ x 4 − x 5 ∣ ) a v g ( C 3 ) = 2 2 × ( 2 − 1 ) × ( ∣ x 6 − x 7 ∣ ) avg(C_1)=\frac{2}{3\times (3-1)}\times(|x_1-x_2|+|x_1-x_3|+|x_2-x_3|) \\ avg(C_2)=\frac{2}{2\times (2-1)}\times(|x_4-x_5|) \\ avg(C_3)=\frac{2}{2\times (2-1)}\times(|x_6-x_7|) avg(C1)=3×(3−1)2×(∣x1−x2∣+∣x1−x3∣+∣x2−x3∣)avg(C2)=2×(2−1)2×(∣x4−x5∣)avg(C3)=2×(2−1)2×(∣x6−x7∣)
diam©–簇内样本的最大距离
d i a m ( C 1 ) = ∣ x 1 − x 3 ∣ d i a m ( C 2 ) = ∣ x 4 − x 5 ∣ d i a m ( C 3 ) = ∣ x 6 − x 7 ∣ diam(C_1)=|x_1-x_3| \\ diam(C_2)=|x_4-x_5| \\ diam(C_3)=|x_6-x_7| diam(C1)=∣x1−x3∣diam(C2)=∣x4−x5∣diam(C3)=∣x6−x7∣
dmin(Ci,Cj)–簇间样本的最小距离
d m i n ( C 1 , C 2 ) = ∣ x 3 − x 4 ∣ d m i n ( C 2 , C 3 ) = ∣ x 5 − x 6 ∣ d m i n ( C 1 , C 3 ) = ∣ x 3 − x 6 ∣ dmin(C_1,C_2)=|x_3-x_4| \\ dmin(C_2,C_3)=|x_5-x_6| \\ dmin(C_1,C_3)=|x_3-x_6| dmin(C1,C2)=∣x3−x4∣dmin(C2,C3)=∣x5−x6∣dmin(C1,C3)=∣x3−x6∣
dcen(Ci,Cj)–簇中心间距离
μ 1 = ( C 1 , C 2 ) = x 1 + x 2 + x 3 3 , μ 2 = x 4 + x 5 2 , μ 3 = x 6 + x 7 2 d c e n ( C 1 , C 2 ) = ∣ μ 1 − μ 2 ∣ d c e n ( C 2 , C 3 ) = ∣ μ 2 − μ 2 ∣ d c e n ( C 1 , C 3 ) = ∣ μ 1 − μ 3 ∣ \mu_1=(C_1,C_2)=\frac{x_1+x_2+x_3}{3},\mu_2=\frac{x_4+x_5}{2},\mu_3=\frac{x_6+x_7}{2} \\ dcen(C_1,C_2)=|\mu_1-\mu_2| \\ dcen(C_2,C_3)=|\mu_2-\mu_2| \\ dcen(C_1,C_3)=|\mu_1-\mu_3| μ1=(C1,C2)=3x1+x2+x3,μ2=2x4+x5,μ3=2x6+x7dcen(C1,C2)=∣μ1−μ2∣dcen(C2,C3)=∣μ2−μ2∣dcen(C1,C3)=∣μ1−μ3∣
DB指数
D B I = 1 k ∑ i = 1 k max j ≠ i ( a v g ( C i ) + a v g ( C j ) d c e n ( μ i , μ j ) ) DBI=\frac{1}{k}\sum_{i=1}^k\max_{j\ne i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)}) DBI=k1i=1∑kj=imax(dcen(μi,μj)avg(Ci)+avg(Cj))
Dunn指数
D I = min 1 ≤ i ≤ k { min j ≠ i ( d m i n ( C i , C j ) max 1 ≤ l ≤ k d i a m ( C l ) } DI=\min_{1\le i\le k}\{\min_{j\ne i}(\frac{d_{min(C_i,C_j)}}{\max_{1\le l\le k}diam(C_l)}\} DI=1≤i≤kmin{j=imin(max1≤l≤kdiam(Cl)dmin(Ci,Cj)}
8.3 距离计算(相似度)
距离越大,相似度越小
样本集合中由 n n n个样本,每个样本由 m m m个属性的特征向量组成,样本集合可以用矩阵 X X X表示:
X = [ x i j ] m × n = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋯ ⋮ x m 1 x m 2 ⋯ x m n ] X=[x_{ij}]_{m\times n}=\begin{bmatrix} x_{11}&x_{12}&\cdots&x_{1n} \\ x_{21}&x_{22}&\cdots&x_{2n} \\ \vdots &\vdots&\cdots&\vdots \\ x_{m1}&x_{m2}&\cdots&x_{mn} \end{bmatrix} X=[xij]m×n=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2⋯⋯⋯⋯x1nx2n⋮xmn⎦⎥⎥⎥⎤
给定样本集合X, x i , x j ∈ X , x i = ( x 1 i , x 2 i , . . . , x m i ) T , x j = ( x 1 j , x 2 j , . . . , x m j ) T x_i,x_j\in X,x_i=(x_{1i},x_{2i},...,x_{mi})^T,x_j=(x_{1j},x_{2j},...,x_{mj})^T xi,xj∈X,xi=(x1i,x2i,...,xmi)T,xj=(x1j,x2j,...,xmj)T
1) 性质
- 非负性 d i j ≥ 0 d_{ij}\ge 0 dij≥0
- 同一性 d i j = 0 d_{ij}=0 dij=0,当且仅当 i = j i=j i=j
- 对称性 d i j = d j i d_{ij}=d_{ji} dij=dji
- 直递性 d i j ≤ d i k + d k j d_{ij}\le d_{ik}+d_{kj} dij≤dik+dkj
2) 闵可夫斯基距离
d i j = ( ∑ k = 1 m ∣ x k i − x k j ∣ p ) 1 p , p ≥ 1 d_{ij}=(\sum_{k=1}^m|x_{ki}-x_{kj}|^p)^{\frac{1}{p}},p\ge 1 dij=(∑k=1m∣xki−xkj∣p)p1,p≥1
欧氏距离
两点之间直线最短
当 p = 2 p=2 p=2时称为欧氏距离(Euclidean distance)
d i j = ( ∑ k = 1 m ∣ x k i − x k j ∣ 2 ) 1 2 d_{ij}=(\sum_{k=1}^m|x_{ki}-x_{kj}|^2)^{\frac{1}{2}} dij=(∑k=1m∣xki−xkj∣2)21
曼哈顿距离
当p=1时称为曼哈顿距离(Manhattan distance)
d i j = ∑ k = 1 m ∣ x k i − x k j ∣ d_{ij}=\sum_{k=1}^m|x_{ki}-x_{kj}| dij=∑k=1m∣xki−xkj∣
切比雪夫距离
当p= ∞ \infty ∞时称为切比雪夫距离(Chebyshev distance)
d i j = m a x k ∣ x k i − x k j ∣ d_{ij}=max_k|x_{ki}-x_{kj}| dij=maxk∣xki−xkj∣
3) 马哈拉诺比斯距离
给定一个样本集 X X X, X = [ x i j ] m × n X=[x_{ij}]_{m \times n} X=[xij]m×n,其协方差矩阵为S,样本 x i x_i xi与样本 x j x_j xj之间的马哈拉诺比斯距离距离 d i j d_{ij} dij定义为
d i j = [ ( x i − x j ) T S − 1 ( x i − x j ) ] 1 2 x i = ( x 1 i , x 2 i , . . . , x m i ) T , x j = ( x 1 j , x 2 j , . . . , x m j ) T d_{ij}=[(x_i-x_j)^TS^{-1}(x_i-x_j)]^{\frac{1}{2}} \\ x_i=(x_{1i},x_{2i},...,x_{mi})^T,x_j=(x_{1j},x_{2j},...,x_{mj})^T dij=[(xi−xj)TS−1(xi−xj)]21xi=(x1i,x2i,...,xmi)T,xj=(x1j,x2j,...,xmj)T
4) 相关系数
样本 x i x_i xi与样本 x j x_j xj之间的相关系数定义为:
r i j = ∑ k = 1 m ( x k i − x ‾ i ) ( x k j − x ‾ j ) [ ∑ k = 1 m ( x k i − x ‾ i ) 2 ∑ k = 1 m ( x k j − x ‾ j ) 2 ] 1 2 x ‾ i = 1 m ∑ k = 1 m x k i , x ‾ j = 1 m ∑ k = 1 m x k j r_{ij}=\frac{\sum_{k=1}^m(x_{ki}-\overline{x}_i)(x_{kj}-\overline{x}_j)}{[\sum_{k=1}^m(x_{ki}-\overline{x}_i)^2\sum_{k=1}^m(x_{kj}-\overline{x}_j)^2]^{\frac{1}{2}}} \\ \overline{x}_i=\frac{1}{m}\sum_{k=1}^mx_{ki},\overline{x}_j=\frac{1}{m}\sum_{k=1}^mx_{kj} rij=[∑k=1m(xki−xi)2∑k=1m(xkj−xj)2]21∑k=1m(xki−xi)(xkj−xj)xi=m1k=1∑mxki,xj=m1k=1∑mxkj
5) 夹角余弦
s i j = ∑ k = 1 m x k i x k j [ ∑ k = 1 m x k i 2 ∑ k = 1 m x k j 2 ] 1 2 s_{ij}=\frac{\sum_{k=1}^mx_{ki}x_{kj}}{[\sum_{k=1}^mx_{ki}^2\sum_{k=1}^mx_{kj}^2]^\frac{1}{2}} sij=[∑k=1mxki2∑k=1mxkj2]21∑k=1mxkixkj
参考资料
https://zhuanlan.zhihu.com/p/100557559
8.4 原型聚类(划分式聚类)
8.4.1 K均值(k-means)
1) 概念
K-means是基于损失函数最小化的思想的,给定样本集 D = { x 1 , x 2 , … , x m } D=\{x_1,x_2,\dots,x_m\} D={x1,x2,…,xm},聚类划分后簇为 C = { c 1 , c 2 , … , c k } C=\{c_1,c_2,\dots,c_k\} C={c1,c2,…,ck},K-means的损失函数定义为:
E = ∑ i = 1 k ∑ x ∈ C i ∣ ∣ x − μ i ∣ ∣ 2 μ i = 1 ∣ C i ∣ ∑ x ∈ C i x E=\sum_{i=1}^k\sum_{x\in C_i}||x-\mu_i||^2 \\ \mu_i=\frac{1}{|C_i|}\sum_{x\in C_i}x E=i=1∑kx∈Ci∑∣∣x−μi∣∣2μi=∣Ci∣1x∈Ci∑x
μ i \mu_i μi 是簇 C i C_i Ci的均值向量
既然要最小化这个东西,那么只要把各个样本归到离自己最近的那个类别就是啦。
说人话就是
样本之间的欧氏距离为 d i j = ∑ k = 1 m ( x k i − x k j ) 2 = ∣ ∣ x i − x j ∣ ∣ 2 d_{ij}=\sum_{k=1}^m(x_{ki}-x_{kj})^2=||x_i-x_j||^2 dij=∑k=1m(xki−xkj)2=∣∣xi−xj∣∣2
损失函数为样本与所属类中心之间距离的总和: W ( C ) = ∑ l = 1 k ∑ C ( i ) = l ∣ ∣ x i − x ‾ l ∣ ∣ 2 W(C)=\sum_{l=1}^k\sum_{C(i)=l}||x_i-\overline{x}_l||^2 W(C)=∑l=1k∑C(i)=l∣∣xi−xl∣∣2
x ‾ l = { x ‾ 1 l , x ‾ 2 l , … , x ‾ m l } \overline{x}_l=\{\overline{x}_{1l},\overline{x}_{2l},\dots,\overline{x}_{ml}\} xl={x1l,x2l,…,xml}为第I类的均值或者中心, W ( C ) W(C) W(C)称为能量函数
k均值聚类就是求解最优化问题: C ∗ = a r g m i n W ( C ) = a r g m i n C ∑ l = 1 k ∑ C ( i ) = l ∣ ∣ x i − x ‾ l ∣ ∣ 2 C^*=argminW(C)=argmin_{C}\sum_{l=1}^k\sum_{C(i)=l}||x_i-\overline{x}_l||^2 C∗=argminW(C)=argminC∑l=1k∑C(i)=l∣∣xi−xl∣∣2
2) 算法推导
输入: n n n个样本的集合 X X X
输出:样本集合的聚类 C ∗ C^* C∗
-
初始化,令 t = 0 t=0 t=0,随机选择 k k k个样本点作为初始聚类中心
m ( 0 ) = ( m 1 ( 0 ) , … , m l ( 0 ) , … , m k ( 0 ) ) m^{(0)}=(m_1^{(0)},\dots,m_l^{(0)},\dots,m_k^{(0)}) m(0)=(m1(0),…,ml(0),…,mk(0))
-
对样本进行聚类,对固定的类中心 m ( t ) = ( m 1 ( t ) , … , m l ( t ) , … , m k ( t ) ) m^{(t)}=(m_1^{(t)},\dots,m_l^{(t)},\dots,m_k^{(t)}) m(t)=(m1(t),…,ml(t),…,mk(t)),其中 m k ( t ) m_k^{(t)} mk(t)为类 C l C_l Cl的中心,
计算每个样本到类中心的距离,将每个样本指派到与其最近的中心的类中,构成聚类结果 C ( t ) C^(t) C(t)
-
计算新的类中心,对聚类结果 C ( t ) C^{(t)} C(t),计算当前各个类中的样本的均值,作为新的类中心
m ( t + 1 ) = ( m 1 ( t + 1 ) , … , m l ( t + 1 ) , … , m k ( t + 1 ) ) m^{(t+1)}=(m_1^{(t+1)},\dots,m_l^{(t+1)},\dots,m_k^{(t+1)}) m(t+1)=(m1(t+1),…,ml(t+1),…,mk(t+1))
-
如果迭代收敛或符合停止条件,输出 C ∗ = C ( t ) C^*=C^{(t)} C∗=C(t),后者令 t = t + 1 t=t+1 t=t+1
算法复杂度 O ( m n k ) O(mnk) O(mnk),其中m为样本维数,n为样本个数,k为类别个数
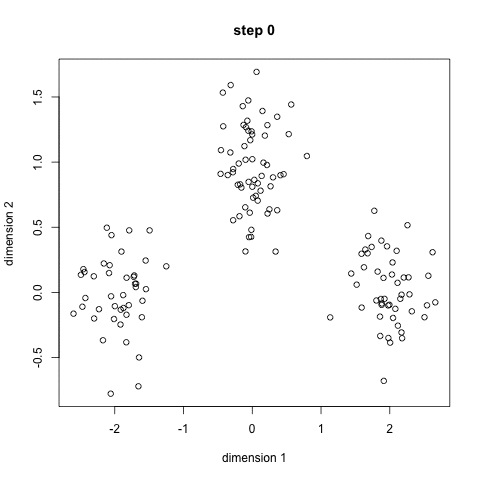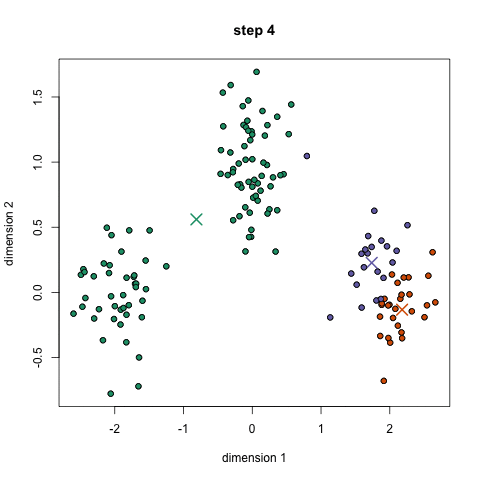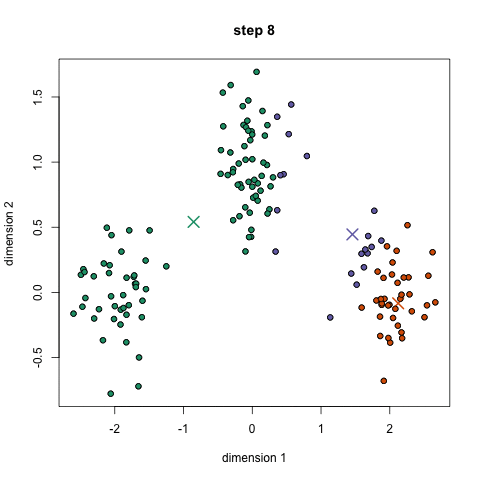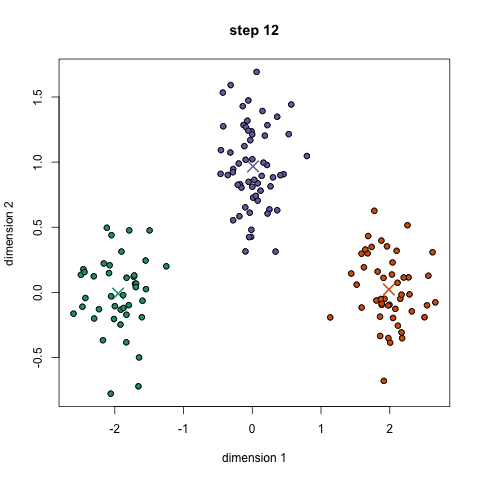
3) 例子
迭代过程
import re
import random
import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt
from time import *
from sklearn.datasets import make_blobs
def find_closet_centroids(X, centroids):
"""
对样本进行分类
"""
result = []
for x in X:
# 计算每个点 到中心点的距离
distance = np.sum((x - centroids) ** 2, axis=1)
# 获取每个点到哪个中心点的位置最小,就划归为哪类
result.append(np.argmin(np.sqrt(distance)))
# print(result)
# [0, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
# 0 表示是第1 类
# 2 表示是第2 类
return np.array(result)
def compute_centroids(X, idx):
"""
计算新的簇中心
"""
# K是一共分成的类数
K = int(np.max(idx)) + 1
# m为X的行数,300,
# n 就是2
m = X.shape[0]
n = X.shape[-1]
# 新的簇中心
centroids = np.zeros((K, n))
# 计算每个簇,有多少个
counts = np.zeros((K,n))
for i in range(m):
centroids[int(idx[i])] += X[i]
counts[int(idx[i])] += 1
# 对簇中心,计算平均值。得到的就是新的簇中心
centroids = centroids / counts
# print(counts)
return centroids
def cost(X, idx, centrodis):
"""
计算损失函数
:param X:
:param idx:
:param centrodis:
:return:
"""
c = 0
for i in range(len(X)):
c += np.sum((X[i] - centrodis[int(idx[i])]) ** 2)
c /= len(X)
return c
def random_initialization(X, K):
"""
随机选择K组数据,作为簇中心
:param X: ndarray,所有点
:param K: int,聚类的类数
:return: ndarray,簇中心
"""
res = np.zeros((1, X.shape[-1]))
m = X.shape[0]
rl = []
while True:
index = random.randint(0, m)
if index not in rl:
rl.append(index)
if len(rl) >= K:
break
for index in rl:
res = np.concatenate((res, X[index].reshape(1, -1)), axis=0)
return res[1:]
def k_means(X, K):
"""
k-means聚类算法,
:param X: ndarray,所有的数据
:param K: int,分成聚类的类数
:return: tuple,(idx, centroids_all)
idx,ndarray 为每个数据所属类标签
centroids_all,[ndarray,...]计算过程中每轮的簇中心
"""
centroids = random_initialization(X, K)
centroids_all = [centroids]
idx = np.zeros((1,))
last_c = -1
now_c = -2
# iterations = 200
# for i in range(iterations):
while now_c != last_c: # 当收敛时结束算法,或者可以利用指定迭代轮数
# 算出每个点所属簇类
idx = find_closet_centroids(X, centroids)
last_c = now_c
# 计算损失函数
now_c = cost(X, idx, centroids)
# 根据重新规划后的簇类,重新规划簇类中心点
centroids = compute_centroids(X, idx)
# 记录训练过程中所有的中心点
centroids_all.append(centroids)
return idx, centroids_all
def visualizing(X, idx, centroids_all):
"""
可视化聚类结果和簇中心的移动过程
:param X: ndarray,所有的数据
:param idx: ndarray,每个数据所属类标签
:param centroids_all: [ndarray,...]计算过程中每轮的簇中心
:return: None
"""
# 绘制图像
plt.scatter(X[..., 0], X[..., 1], c=idx)
xx = []
yy = []
for c in centroids_all:
xx.append(c[..., 0])
yy.append(c[..., 1])
plt.plot(xx, yy, 'rx--')
plt.show()
if __name__ == '__main__':
begin_time = time()
print("========程序开始============")
# data = sio.loadmat("ex7data2.mat")
# X = np.array(data['X']) # (300,2)
# 随机生成5组数据
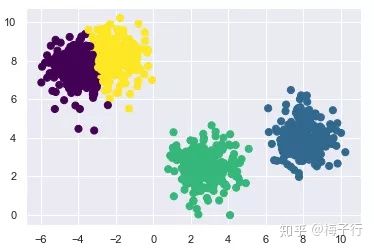
X, y = make_blobs(centers=5, random_state=20, cluster_std=1)
# print(x)
idx, centroids_all = k_means(X, 5)
visualizing(X, idx, centroids_all)
end_time = time()
run_time = end_time - begin_time
print("========程序结束============")
print('该循环程序运行时间:', run_time)
4) 优缺点
优点:
原理比较简单,实现也是很容易,收敛速度快;聚类效果较优;算法的可解释度比较强;主要需要调参的参数仅仅是簇数k。
缺点:
1、聚类中心的个数K需要事先给定,这个K值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适;一般通过交叉验证确定;
2、不同的初始聚类中心可能导致完全不同的聚类结果。算法速度依赖于初始化的好坏,初始质点距离不能太近;
3、如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳;
4、该方法不适于发现非凸面形状的簇或大小差别很大的簇,对于不是凸的数据集比较难收敛;
5、对噪音和异常点比较的敏感。
6、需样本存在均值(限定数据种类)。
7、采用迭代方法,得到的结果只是局部最优。
8.4.2 LVQ
8.4.3 高斯混合聚类GMM
1) 介绍
高斯混合模型(GMM)可以看做是k-means模型的一个优化。它既是一种工业界常用的技术手段,也是一种生成式模型。
高斯混合模型试图找到多维高斯模型概率分布的混合表示,从而拟合出任意形状的数据分布。在最简单的场景中,GMM可以用与k-means相同的方式进行聚类。
只是将高斯分布、贝叶斯公式、极大似然法和聚类的思路混合在这一种方法中,容易被绕来绕去感到云里雾里的。
2) 数学准备
a) 高斯分布
首先是高斯分布的概念。高斯分布即正态分布。一般我们最常见最熟知的一元正态分布的标准形式和曲线是这样的:
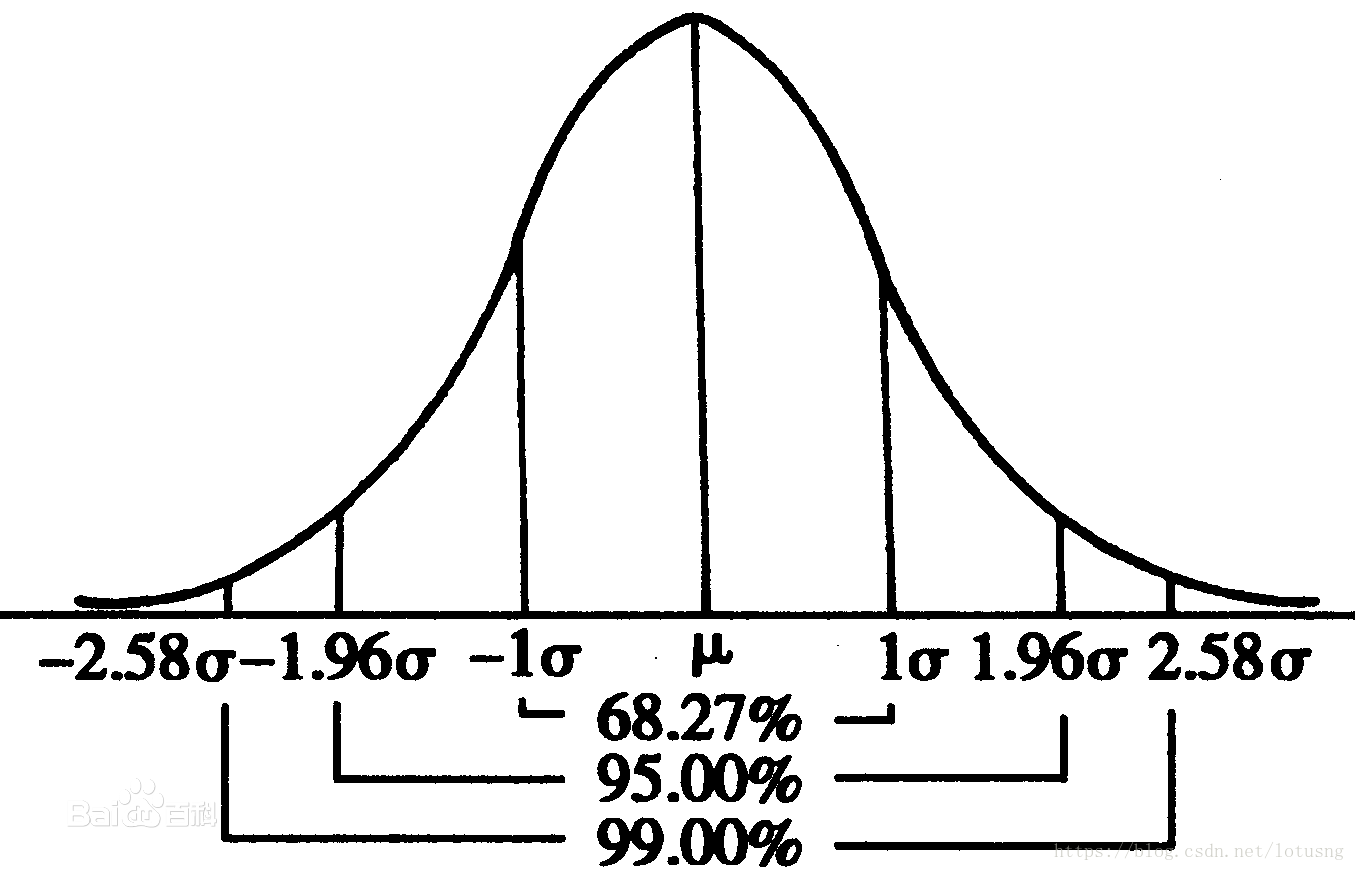
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2
正态分布可以记为 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2),从上面的公式很明显可以看出一元正态分布只有两个参数 μ \mu μ和 σ \sigma σ,且这两个参数决定了正态曲线的“宽窄”、“高矮”。 曲线下面积为1。
b) 多元高斯分布
资料参考
https://www.cnblogs.com/bingjianing/p/9117330.html
https://www.zhihu.com/question/36339816
先假设n个变量 x = [ x 1 , x 2 , … , x n ] T x=[x_1,x_2,\dots,x_n]^T x=[x1,x2,…,xn]T,且服从正态分布(维度不相关多元正态分布),
各个维度的均值 E ( x ) = [ μ 1 , μ 2 , … , μ n ] T E(x)=[\mu_1,\mu_2,\dots,\mu_n]^T E(x)=[μ1,μ2,…,μn]T,
方差 σ ( x ) = [ σ 1 , σ 2 , … , σ n ] T \sigma(x)=[\sigma_1,\sigma_2,\dots,\sigma_n]^T σ(x)=[σ1,σ2,…,σn]T
根据联合概率密度公式:
f ( x ) = p ( x 1 , x 2 , … , x n ) = p ( x 1 ) p ( x 2 ) … p ( x n ) = 1 ( 2 π ) n σ 1 σ 2 … σ n e − ( x 1 − μ 1 ) 2 2 σ 1 2 − ( x 2 − μ 2 ) 2 2 σ 2 2 ⋯ − ( x n − μ n ) 2 2 σ n 2 f(x)=p(x_1,x_2,\dots,x_n)=p(x_1)p(x_2)\dots p(x_n) \\ =\frac{1}{(\sqrt{2\pi})^n\sigma_1\sigma_2\dots\sigma_n}e^{-\frac{(x_1-\mu_1)^2}{2\sigma_1^2}-\frac{(x_2-\mu_2)^2}{2\sigma_2^2}\dots-\frac{(x_n-\mu_n)^2}{2\sigma_n^2}} f(x)=p(x1,x2,…,xn)=p(x1)p(x2)…p(xn)=(2π)nσ1σ2…σn1e−2σ12(x1−μ1)2−2σ22(x2−μ2)2⋯−2σn2(xn−μn)2
令 z 2 = − ( x 1 − μ 1 ) 2 2 σ 1 2 − ( x 2 − μ 2 ) 2 2 σ 2 2 ⋯ − ( x n − μ n ) 2 2 σ n 2 , σ z = σ 1 σ 2 … σ n 令z^2=-\frac{(x_1-\mu_1)^2}{2\sigma_1^2}-\frac{(x_2-\mu_2)^2}{2\sigma_2^2}\dots-\frac{(x_n-\mu_n)^2}{2\sigma_n^2},\sigma_z=\sigma_1\sigma_2\dots\sigma_n 令z2=−2σ12(x1−μ1)2−2σ22(x2−μ2)2⋯−2σn2(xn−μn)2,σz=σ1σ2…σn
这样多元正态分布又可以写成一元那种漂亮的形式了(注意一元与多元的差别):
f ( z ) = 1 ( 2 π ) n σ n e − z 2 2 f(z)=\frac{1}{(\sqrt{2\pi})^n\sigma_n}e^{-\frac{z^2}{2}} f(z)=(2π)nσn1e−2z2
因为多元正态分布有着很强的几何思想,单纯从代数的角度看待z很难看出z的概率分布规律,这里需要转换成矩阵形式:
z 2 = z T z = [ x 1 − μ 1 , x 2 − μ 2 , … , x n − μ n ] [ 1 σ 1 2 0 … 0 0 1 σ 2 2 … 0 ⋮ … … ⋮ 0 0 … 1 σ n 2 ] [ x 1 − μ 1 , x 2 − μ 2 , … , x n − μ n ] T z^2=z^Tz=[x_1-\mu_1,x_2-\mu_2,\dots,x_n-\mu_n] \begin{bmatrix} \frac{1}{\sigma_1^2}&0&\dots&0 \\ 0&\frac{1}{\sigma_2^2}&\dots&0 \\ \vdots&\dots&\dots&\vdots \\ 0&0&\dots&\frac{1}{\sigma_n^2} \end{bmatrix} [x_1-\mu_1,x_2-\mu_2,\dots,x_n-\mu_n]^T z2=zTz=[x1−μ1,x2−μ2,…,xn−μn]⎣⎢⎢⎢⎢⎡σ1210⋮00σ221…0…………00⋮σn21⎦⎥⎥⎥⎥⎤[x1−μ1,x2−μ2,…,xn−μn]T
等式比较长,让我们要做一下变量替换:
x − μ x = [ x 1 − μ 1 , x 2 − μ 2 , … , x n − μ n ] T x-\mu_x=[x_1-\mu_1,x_2-\mu_2,\dots,x_n-\mu_n]^T x−μx=[x1−μ1,x2−μ2,…,xn−μn]T
定义一个符号
∑ = [ σ 1 2 0 … 0 0 σ 2 2 … 0 ⋮ … … ⋮ 0 0 … σ n 2 ] \sum=\begin{bmatrix}\sigma_1^2&0&\dots&0\\ 0&\sigma_2^2&\dots&0\\ \vdots&\dots&\dots&\vdots\\ 0&0&\dots&\sigma_n^2\end{bmatrix} ∑=⎣⎢⎢⎢⎡σ120⋮00σ22…0…………00⋮σn2⎦⎥⎥⎥⎤
∑ \sum ∑代表变量 X X X的协方差矩阵, i行j列的元素值表示 x i 与 x j x_i与x_j xi与xj的协方差
因为现在变量之间是相互独立的,所以只有对角线上 ( i = j ) (i = j) (i=j)存在元素,其他地方都等于0,且 x i x_i xi与它本身的协方差就等于方差
∑ \sum ∑是一个对角阵,根据对角矩阵的性质,它的逆矩阵:
( ∑ ) − 1 = [ 1 σ 1 2 0 … 0 0 1 σ 2 2 … 0 ⋮ … … ⋮ 0 0 … 1 σ n 2 ] (\sum)^{-1}=\begin{bmatrix} \frac{1}{\sigma_1^2}&0&\dots&0 \\ 0&\frac{1}{\sigma_2^2}&\dots&0 \\ \vdots&\dots&\dots&\vdots \\ 0&0&\dots&\frac{1}{\sigma_n^2} \end{bmatrix} (∑)−1=⎣⎢⎢⎢⎢⎡σ1210⋮00σ221…0…………00⋮σn21⎦⎥⎥⎥⎥⎤
对角矩阵的行列式 = 对角元素的乘积
σ z = ∣ ∑ ∣ 1 2 = σ 1 σ 2 … σ n \sigma_z=|\sum|^{\frac{1}{2}}=\sigma_1\sigma_2\dots\sigma_n σz=∣∑∣21=σ1σ2…σn
替换变量之后,等式可以简化为:
z T z = ( x − μ x ) T ∑ 1 2 ( x − μ x ) z^Tz=(x-\mu_x)^T\sum^{\frac{1}{2}}(x-\mu_x) zTz=(x−μx)T∑21(x−μx)
代入以z为自变量的标准高斯分布函数中:
一般的多元高斯具有形式:
f ( z ) = 1 ( 2 π ) n σ n e − z 2 2 f ( x ) = 1 ( 2 π ) n ∣ ∑ ∣ 1 2 e − ( x − μ x ) T ( ∑ ) − 1 ( x − μ x ) 2 f(z)=\frac{1}{(\sqrt{2\pi})^n\sigma_n}e^{-\frac{z^2}{2}} \\ f(x)=\frac{1}{(\sqrt{2\pi})^n|\sum|^{\frac{1}{2}}}e^{-\frac{(x-\mu_x)^T(\sum)^{-1}(x-\mu_x)}{2}} f(z)=(2π)nσn1e−2z2f(x)=(2π)n∣∑∣211e−2(x−μx)T(∑)−1(x−μx)
注意前面的系数变化:从非标准正态分布->标准正态分布需要将概率密度函数的高度压缩 ∣ ∑ ∣ 1 2 |\sum|^{\frac{1}{2}} ∣∑∣21倍, 从一维 -> n维的过程中,每增加一维,高度将压缩 2 π \sqrt{2\pi} 2π倍
二元高斯曲线如下图。曲线下面积为1。它多了一个变量。例如x轴是身高,y轴是体重,有了身高体重的数据就可以在z轴找到该身高体重在人群中所占的比例(即概率)。同样地,中等身高且中等体重的人在人群中是最常见的,正如路上普普通通的路人。
c) 贝叶斯公式
P ( A i ∣ B ) = P ( A i ) P ( B ∣ A i ) ∑ j = 1 n P ( A j ) P ( B ∣ A j ) P(A_i|B)=\frac{P(A_i)P(B|A_i)}{\sum_{j=1}^nP(A_j)P(B|A_j)} P(Ai∣B)=∑j=1nP(Aj)P(B∣Aj)P(Ai)P(B∣Ai)
d) 极大似然
2) 算法推导
n维样本的高斯分布为:
p ( x ) = 1 ( 2 π ) n ∣ ∑ ∣ 1 2 e − ( x − μ x ) T ( ∑ ) − 1 ( x − μ x ) 2 p(x)=\frac{1}{(\sqrt{2\pi})^n|\sum|^{\frac{1}{2}}}e^{-\frac{(x-\mu_x)^T(\sum)^{-1}(x-\mu_x)}{2}} p(x)=(2π)n∣∑∣211e−2(x−μx)T(∑)−1(x−μx)
由贝叶斯定理,样本 x j x_j xj属于 i i i类的后验概率为:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p_M(z_j=i|x_j)…
将上式简写为 γ j i \gamma_{ji} γji
则样本 x j x_j xj分类公式为
λ j = a r g m a x i ∈ { 1 , 2 , … , k } γ j i \lambda_j=argmax_{i\in \{1,2,\dots,k\}}\gamma_{ji} λj=argmaxi∈{1,2,…,k}γji
给每一个分类一个系数,采用对数似然,得
L L ( D ) = l n ( ∏ j = 1 m P M ( x j ) ) ∑ j = 1 m l n ( ∑ i = 1 k α i ⋅ P ( x j ∣ μ i , ∑ i ) ) LL(D)=ln(\prod_{j=1}^mP_M(x_j)) \\ \sum_{j=1}^mln(\sum_{i=1}^k\alpha_i\cdot P(x_j|\mu_i,\sum_i)) LL(D)=ln(j=1∏mPM(xj))j=1∑mln(i=1∑kαi⋅P(xj∣μi,i∑))
上式分别对 ∑ , μ \sum,\mu ∑,μ求导。令导数为0,得
μ i = ∑ j = 1 m γ j i x j ∑ j = 1 m γ j i ∑ i = ∑ j = 1 m γ j i ( x j − μ i ) ( x j − μ i ) T ∑ j = 1 m γ j i \mu_i=\frac{\sum_{j=1}^m\gamma_{ji}x_j}{\sum_{j=1}^m\gamma_{ji}} \\ \sum_i=\frac{\sum_{j=1}^m\gamma_{ji}(x_j-\mu_i)(x_j-\mu_i)^T}{\sum_{j=1}^m\gamma_{ji}} μi=∑j=1mγji∑j=1mγjixji∑=∑j=1mγji∑j=1mγji(xj−μi)(xj−μi)T
系数求和为1,引入此约束,对数似然的拉格朗日形式为
α i = 1 m ∑ j = 1 m γ j i \alpha_i=\frac{1}{m}\sum_{j=1}^m\gamma_{ji} αi=m1∑j=1mγji
3) 例子
代码
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
#产生实验数据
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=700, centers=4,
cluster_std=0.5, random_state=2019)
X = X[:, ::-1] #方便画图
from sklearn.mixture import GaussianMixture as GMM
gmm = GMM(n_components=4).fit(X) #指定聚类中心个数为4
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
它使用EM算法进行迭代:1.选择位置和初始形状2.循环直至收敛:
E步骤:对于每个点,为每个点分别计算由该混合模型内的每个分量生成的概率。
M步骤:调整模型参数以最大化模型生成这些参数的可能性。
该算法保证该过程内的参数总会收敛到一个局部最优解。
例二
参考资料
https://www.cnblogs.com/lunge-blog/p/11792226.html
数据
序号,密度,含糖量
1,0.697,0.460
2,0.774,0.376
3,0.634,0.264
4,0.608,0.318
5,0.556,0.215
6,0.403,0.237
7,0.481,0.149
8,0.437,0.211
9,0.666,0.091
10,0.243,0.267
11,0.245,0.057
12,0.343,0.099
13,0.639,0.161
14,0.657,0.198
15,0.360,0.370
16,0.593,0.042
17,0.719,0.103
18,0.359,0.188
19,0.339,0.241
20,0.282,0.257
21,0.748,0.232
22,0.714,0.346
23,0.483,0.312
24,0.478,0.437
25,0.525,0.369
26,0.751,0.489
27,0.532,0.472
28,0.473,0.376
29,0.725,0.445
30,0.446,0.459
代码
file='xigua4.txt'
x=[]
with open(file) as f:
f.readline()
lines=f.read().split('\n')
for line in lines:
data=line.split(',')
x.append([float(data[-2]),float(data[-1])])
y=np.array(x)
# 2 算法部分
import numpy as np
import random
def probability(x,u,cov):
cov_inv=np.linalg.inv(cov)
cov_det=np.linalg.det(cov)
return np.exp(-1/2*((x-u).T.dot(cov_inv.dot(x-u))))/np.sqrt(cov_det)
def gauss_mixed_clustering(x,k=3,epochs=50,reload_params=None):
features_num=len(x[0])
r=np.empty(shape=(len(x),k))
# 初始化系数,均值向量和协方差矩阵
if reload_params!=None:
a,u,cov=reload_params
else:
a=np.random.uniform(size=k)
a/=np.sum(a)
u=np.array(random.sample(list(x),k))
cov=np.empty(shape=(k,features_num,features_num))
# 初始化为只有对角线不为0
for i in range(k):
for j in range(features_num):
cov[i][j]=[0]*j+[0.5]+[0]*(features_num-j-1)
step=0
while step<epochs:
# E步:计算r_ji
for j in range(len(x)):
for i in range(k):
r[j,i]=a[i]*probability(x[j],u[i],cov[i])
r[j]/=np.sum(r[j])
for i in range(k):
r_toal=np.sum(r[:,i])
u[i]=np.sum([x[j]*r[j,i] for j in range(len(x))],axis=0)/r_toal
cov[i]=np.sum([r[j,i]*((x[j]-u[i]).reshape((features_num,1)).dot((x[j]-u[i]).reshape((1,features_num)))) for j in range(len(x))],axis=0)/r_toal
a[i]=r_toal/len(x)
step+=1
C=[]
for i in range(k):
C.append([])
for j in range(len(x)):
c_j=np.argmax(r[j,:])
C[c_j].append(x[j])
return C,a,u,cov
验证
res,A,U,COV=gauss_mixed_clustering(y)
import matplotlib.pyplot as plt
%matplotlib inline
colors=['green','blue','red','black','yellow','orange']
for i in range(len(res)):
plt.scatter([d[0] for d in res[i]],[d[1] for d in res[i]],color=colors[i],label=str(i))
plt.scatter([d[0] for d in U],[d[1] for d in U],color=colors[-1],marker='^',label='center')
plt.xlabel('density')
plt.ylabel('suger')
plt.legend()
50论过后
res,A,U,COV=gauss_mixed_clustering(y,reload_params=[A,U,COV])
for i in range(len(res)):
plt.scatter([d[0] for d in res[i]],[d[1] for d in res[i]],color=colors[i],label=str(i))
plt.scatter([d[0] for d in U],[d[1] for d in U],color=colors[-1],marker='^',label='center')
plt.xlabel('density')
plt.ylabel('suger')
plt.legend()
参考资料
https://zhuanlan.zhihu.com/p/81255623
https://blog.csdn.net/lotusng/article/details/79990724
8.5 密度聚类
8.5.1 概念
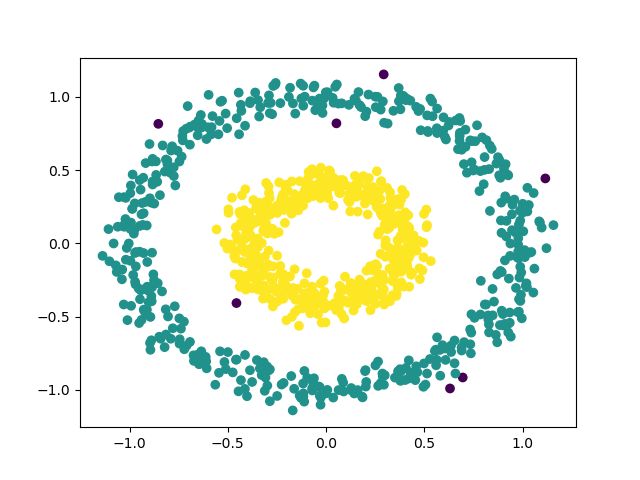
k-means算法对于凸性数据具有良好的效果,能够根据距离来讲数据分为球状类的簇,但对于非凸形状的数据点,就无能为力了,当k-means算法在环形数据的聚类时,我们看看会发生什么情况。
从上图可以看到,kmeans聚类产生了错误的结果,这个时候就需要用到基于密度的聚类方法了,
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法,类似于均值转移聚类算法,但它有几个显著的优点。
DBSCAN算法的核心思想是:用一个点的ε邻域内的邻居点数衡量该点所在空间的密度,该算法可以找出形状不规则的cluster,而且聚类的时候事先不需要给定cluster的数量。
常用的密度聚类算法:DBSCAN、MDCA、OPTICS、DENCLUE等。
密度聚类的主要特点是:
- 发现任意形状的簇
- 对噪声数据不敏感
- 一次扫描
- 需要密度参数作为停止条件
- 计算量大、复杂度高
8.5.2 相关概念
定义一个数据集 D = { x 1 , x 2 , … , x m } D=\{x_1,x_2,\dots,x_m\} D={x1,x2,…,xm}
-
ϵ \epsilon ϵ 表示半径
-
ϵ \epsilon ϵ领域( ϵ \epsilon ϵ neighborhood,也称为Eps),给定对象在半径 ϵ \epsilon ϵ内的区域
N ϵ ( x ) = { y ∈ X : d i s t ( x , y ) ≤ ϵ } N_\epsilon(x)=\{y\in X:dist(x,y)\le \epsilon\} Nϵ(x)={y∈X:dist(x,y)≤ϵ}
-
密度
ϵ \epsilon ϵ领域中x的密度,是一个整数值,依赖于半径 ϵ \epsilon ϵ
p ( x ) = ∣ N ϵ ( x ) ∣ p(x)=|N_\epsilon(x)| p(x)=∣Nϵ(x)∣
-
MinPts
ε-邻域内样本个数最小值。也简记为M
-
核心对象
若 x i x_i xi的 ϵ \epsilon ϵ领域至少包含MinPts个样本,即| N ϵ ( x i ) ∣ ≥ M i n P t s N_\epsilon(x_i)|\ge MinPts Nϵ(xi)∣≥MinPts,则 x i x_i xi是一个核心对象
-
密度直达
若 x j x_j xj位于 x i x_i xi的 ϵ \epsilon ϵ领域中,且 x i x_i xi是核心对象,则称 x j x_j xj和 x i x_i xi是密度直达
-
密度可达(density-reachable)
如果存在一个对象链 p 1 , p 2 , . . p m p_1,p_2,..p_m p1,p2,..pm,其中 p 1 = x i , p n = x j , p_1=x_i,p_n=x_j, p1=xi,pn=xj,且 p i + 1 p_{i+1} pi+1由 p i p_i pi密度直达,那么称 x j x_j xj是从 x i x_i xi密度可达的。
-
密度相连(density-connected)
在集合X中,如果存在一个对象o,使得对象x和y是从o关于ε和m密度可达的,那么对象x和y是关于ε和m密度相连的。
可以发现,密度可达是直接密度可达的传递闭包,并且这种关系是非对称的。密度相连是对称关系。DBSCAN目的是找到密度相连对象的最大集合。
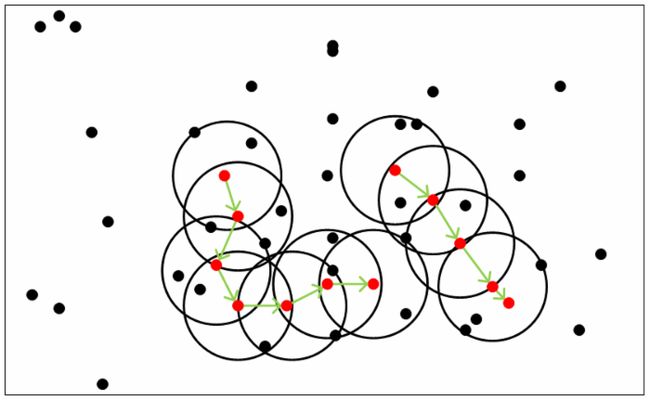
从下图可以很容易看出理解上述定义,图中MinPts=5,红色的点都是核心对象,因为其ϵ-邻域至少有5个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内,如果不在超球体内,则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的ϵ-邻域内所有的样本相互都是密度相连的。
8.5.3 DBSCAN算法推导
1、如果一个点x的ε邻域包含多余m个对象,则创建一个x作为核心对象的新簇;
2、寻找并合并核心对象直接密度可达的对象;
3、没有新点可以更新簇的时候,算法结束。
输入:样本集 D = { x 1 , x 2 , … , x m } D=\{x_1,x_2,\dots,x_m\} D={x1,x2,…,xm},领域参数 ( ϵ , M i n P t s ) (\epsilon,MinPts) (ϵ,MinPts),样本距离度量方式
输出:簇划分
初始化核心对象集合 Ω = ϕ \Omega=\phi Ω=ϕ,初始化聚类簇k=0,初始化为访问样本集合 F F F.簇划分 C = ϕ C=\phi C=ϕ
对于j=1,2,…,m,按照下面的步骤找出所有的核心对象
a) 通过距离度量的方式没找到样本 x j x_j xj的 ϵ \epsilon ϵ领域子样本集 N ϵ ( x j ) N_\epsilon(x_j) Nϵ(xj)
b) 如果子样本集样本个数满足 ∣ N ϵ ( x j ) ∣ ≥ M i n P t s |N_\epsilon(x_j)|\ge MinPts ∣Nϵ(xj)∣≥MinPts,将样本 x j x_j xj加入核心对象样本集合 Ω = Ω ⋃ { x j } \Omega=\Omega \bigcup\{x_j\} Ω=Ω⋃{xj}
如果核心对象集合 Ω = ϕ \Omega=\phi Ω=ϕ,则算法结束,否则转入步骤4
在核心对象集合Ω中,随机选择一个核心对象o,初始化当前簇核心对象队列 Ω c u r r e n t = { o } \Omega_{current}=\{o\} Ωcurrent={o},初始化类别序号k=k+1,初始化当前簇样本集合 C k = { o } C_k=\{o\} Ck={o},更新未访问核心对象为未访问集合 F = F − { o } F=F-\{o\} F=F−{o}。
如果当前簇核心对象队列 Ω c u r r e n t = ϕ \Omega_{current}=\phi Ωcurrent=ϕ,则当前聚类簇 C k C_k Ck生成完毕,更新簇划分 C = { C 1 , C 2 , . . C k } C=\{C_1,C_2,..C_k\} C={C1,C2,..Ck},更新核心对象集合 Ω = Ω − C k \Omega=\Omega-C_k Ω=Ω−Ck,转入步骤3,否则更新核心对象集合 Ω = Ω − C k \Omega=\Omega-C_k Ω=Ω−Ck。
在当前簇核心对象队列 Ω c u r r e n t \Omega_{current} Ωcurrent中取出一个核心对象 o ′ o^\prime o′。通过领域距离阈值 ϵ 领 域 \epsilon领域 ϵ领域子样本集 N ϵ ( o ′ ) N_\epsilon(o^\prime) Nϵ(o′),令 Δ = N ϵ ( o ′ ) ⋂ F \Delta=N_\epsilon(o^\prime)\bigcap F Δ=Nϵ(o′)⋂F,更新当前簇集合 C k = C k ⋃ Δ C_k=C_k\bigcup \Delta Ck=Ck⋃Δ,更新为访问样本集合 F = F − Δ F=F-\Delta F=F−Δ,更新 Ω c u r r e n t = Ω c u r r e n t ⋃ ( Δ ⋂ Ω ) − o ′ \Omega_{current}=\Omega_{current}\bigcup (\Delta\bigcap \Omega)-o^\prime Ωcurrent=Ωcurrent⋃(Δ⋂Ω)−o′,转入步骤5
输出结果,簇划分 C = { C 1 , C 2 , . . . , C k } C=\{C_1,C_2,...,C_k\} C={C1,C2,...,Ck}
算法特征描述:
1、每个簇至少包含一个核心对象。
2、非核心对象可以是簇的一部分,构成簇的边缘。
3、包含过少对象的簇被认为是噪声。
8.5.4 代码
import re
import random
from sklearn.cluster import DBSCAN
import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt
from time import *
from sklearn.datasets import make_blobs
from sklearn import datasets
def dbscan(data_set, eps, min_pts):
"""
data_set 数据集,[n,2]
eps 邻域大小范围
min_pts 一个邻域至少包含多少个样本
"""
examples_nus = np.shape(data_set)[0] # 样本数量
unvisited = [i for i in range(examples_nus)] # 未被访问的点
visited = [] # 已被访问的点
# cluster为输出结果,表示对应元素所属类别
# 默认是一个长度为examples_nus的值全为-1的列表,-1表示噪声点
cluster = [-1 for i in range(examples_nus)]
k = - 1 # 用k标记簇号,如果是-1表示是噪声点
while len(unvisited) > 0: # 只要还有没有被访问的点就继续循环
p = random.choice(unvisited) # 随机选择一个未被访问对象
unvisited.remove(p)
visited.append(p)
nighbor = [] # nighbor为p的eps邻域对象集合,密度直接可达
for i in range(examples_nus):
if i != p and np.sqrt(np.sum(np.power(data_set[i, :] - data_set[p, :], 2))) <= eps: # 计算距离,看是否在邻域内
nighbor.append(i)
if len(nighbor) >= min_pts: # 如果邻域内对象个数大于min_pts说明是一个核心对象
k = k + 1
cluster[p] = k # 表示p它属于k这个簇
for pi in nighbor: # 现在要找该邻域内密度可达
if pi in unvisited:
unvisited.remove(pi)
visited.append(pi)
# nighbor_pi是pi的eps邻域对象集合
nighbor_pi = []
for j in range(examples_nus):
if np.sqrt(np.sum(np.power(data_set[j] - data_set[pi], 2))) <= eps and j != pi:
nighbor_pi.append(j)
if len(nighbor_pi) >= min_pts: # pi是否是核心对象,通过他的密度直接可达产生p的密度可达
for t in nighbor_pi:
if t not in nighbor:
nighbor.append(t)
if cluster[pi] == -1: # pi不属于任何一个簇,说明第pi个值未改动
cluster[pi] = k
else:
cluster[p] = -1 # 不然就是一个噪声点
return np.array(cluster)
if __name__ == '__main__':
# centers = [[1, 1], [-1, -1], [1, -1]]
# 生成非凸数据 factor表示内外圈距离比
X, Y1 = datasets.make_circles(n_samples=1000, factor=.4, noise=.07)
print(X)
eps = 0.1 # 邻域半径
min_pts = 2 # 核心对象
cluster = dbscan(X, eps, min_pts)
print(cluster.shape)
print(np.unique(cluster))
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=cluster)
plt.show()
plt.figure()
y_pred = DBSCAN(eps=0.1).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
结果如下
想要换个模型
X, Y1 = datasets.make_moons(n_samples=200, noise=None, shuffle=True, random_state=None)
可以自己玩
datasets.make_biclusters() # 为双聚类生成具有常数块对角结构的数组。
datasets.make_blobs() # 生成用于聚类的各向同性高斯斑点。
datasets.make_checkerboard() # 为双聚类生成具有方块棋盘结构的数组。
datasets.make_circles() # 在2维中制作一个包含一个小圆的大圆。
datasets.make_classification() # 生成一个随机n类分类问题。
datasets.make_friedman1() # 生成“Friedman#1”回归问题。
datasets.make_friedman2() # 生成“Friedman#2”回归问题。
datasets.make_friedman3() # 生成“Friedman#3”回归问题。
datasets.make_gaussian_quantiles() # 生成各向同性高斯并按分位数标记样本。
datasets.make_hastie_10_2() # 为Hastine等人使用的二进制分类生成数据。
datasets.make_low_rank_matrix() # 生成具有钟形奇异值的低秩矩阵。
datasets.make_moons() # 做两个交叉的半圆。
datasets.make_multilabel_classification() # 生成一个随机多标签分类问题。
datasets.make_regression() # 生成一个随机回归问题。
datasets.make_s_curve() # 生成S曲线数据集。
datasets.make_sparse_coded_signal() # 将信号生成为字典元素的稀疏组合。
datasets.make_sparse_spd_matrix() # 生成稀疏对称正定矩阵。
datasets.make_sparse_uncorrelated() # 生成具有稀疏不相关设计的随机回归问题。
datasets.make_spd_matrix() # 生成一个随机对称正定矩阵。
datasets.make_swiss_roll() # 生成瑞士卷数据集。
8.5.5 优缺点
**优点:**不需要确定要划分的聚类个数,聚类结果没有偏倚;抗噪声,在聚类的同时发现异常点,对数据集中的异常点不敏感;处理任意形状和大小的簇,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
**缺点:**数据量大时内存消耗大,相比K-Means参数多一些;样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合;
参考资料
https://www.jianshu.com/p/5e5bcf3ec9d6
(3条消息) python实现DBSCAN聚类_啃西瓜的小煤球的博客-CSDN博客_dbscan聚类python实现
8.6 层次聚类
8.6.1 概念
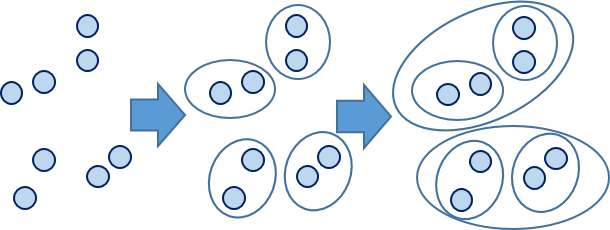
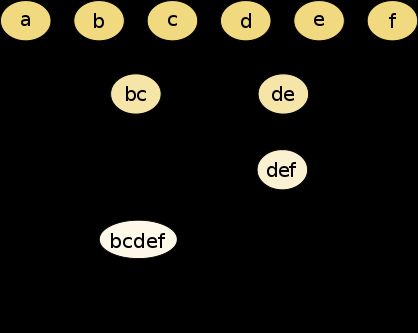
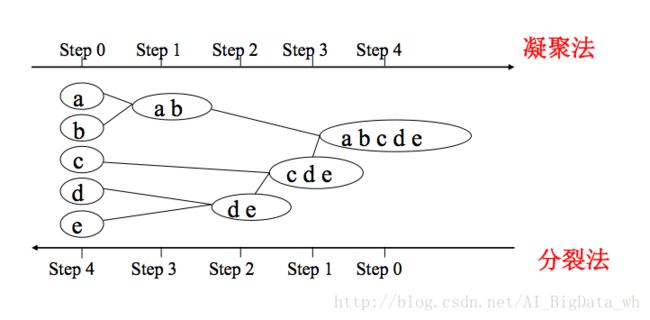
层次聚类(Hierarchical Clustering)是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法,本篇文章介绍合并方法
源数据:
层次聚类:
1.凝聚层次聚类:AGNES算法(自底向上)
首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到某个终结条件被满足
2.分裂层次聚类:DIANA算法(自顶向下)
首先将所有对象置于一个簇中,然后逐渐细分为越来越小的簇,直到达到了某个终结条件。
8.6.2 数学准备
给定聚类簇 C i C_i Ci和 C j C_j Cj,两个簇的距离可以通过以下定义得到
最短距离: d m i n ( C i , C j ) = m i n p ∈ C i , q ∈ C j ∣ p − q ∣ d_{min}(C_i,C_j)=min_{p\in C_i,q\in C_j}|p-q| dmin(Ci,Cj)=minp∈Ci,q∈Cj∣p−q∣
最大距离 d m a x ( C i , C j ) = m a x p ∈ i , q ∈ C j ∣ p − q ∣ d_{max}(C_i,C_j)=max_{p\in _i,q\in C_j}|p-q| dmax(Ci,Cj)=maxp∈i,q∈Cj∣p−q∣
均值距离 d m e a n ( C i , C j ) = ∣ p ‾ − q ‾ ∣ , 其 中 p ‾ = 1 ∣ C i ∣ ∑ p ∈ C i p , q ‾ = ∑ q ∈ C j q d_{mean}(C_i,C_j)=|\overline{p}-\overline{q}|,其中\overline{p}=\frac{1}{|C_i|}\sum_{p\in C_i}p,\overline{q}=\sum_{q\in C_j}q dmean(Ci,Cj)=∣p−q∣,其中p=∣Ci∣1∑p∈Ci