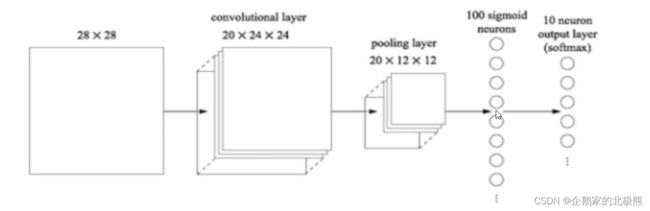
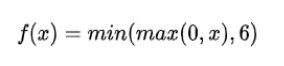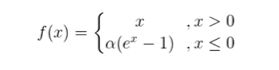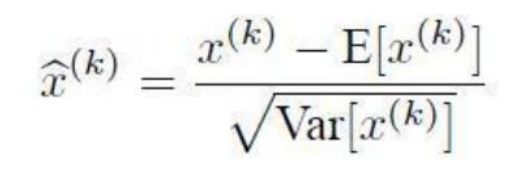深度学习——神经网络之CNN卷积神经网络

深度学习——神经网络之CNN卷积神经网络

本篇文章开始介绍卷积神经网络，卷积神经网络分为很多种，在后面的《高阶段卷积》章节介绍，这个、里主要介绍卷积神经网络用到的基础知识。所有负责的模型都是根据简单的模型优化而来的。

1、回顾神经网络知识

1.1、BP神经网络回顾

第一个问题：为什么有了BP神经网（DNN网络中有介绍）络还要有深度学习？

• BP神经网络不适合深层的模型，太深以后BP反向传播过程中容易造成梯度消失或者梯度暴涨，只适合浅层的
• 算力问题，没有GPU，CUP算力不够，随着深度的加深，参数的增多，模型训练困难，时间长。

第二个问题：影响模型复杂程度的因素

• 隐含层的层数
• 单个隐含层的神经元个数

这两个因素都是影响模型参数的条件，后期优化模型的思路大多也是从这两个方面做得优化，层而产生新的模型。

1.2、激活函数

• Sigmoid函数的缺点，从图中可以看出，Sigmoid激活函数具有饱和区域，随着值的增加，到一定程度时，函数的值趋向于1,0，这样就会造成梯度消失（为0）,模型收敛不了。
• tanh同Sigmoid一样，也具有饱和区。
• Relu:更多用于图像模型，后面的好多激活函数都是在这个激活函数上优化的，优化的就是他的缺点——>当值为负数（权重为负数）的时候，直接置为0了
• Leaky ReLU：在Relu上做的改进，当值为负数的时候，加上一个0.1的斜率（乘0.1）
• Maxout，ELU也是分段函数，对Relu做一个改进

2、卷积神经网络

第一个问题：为什么有了DNN神经网络，RNN神经网络，BP神经网络，还要CNN神经网络？

• 对于图像得处理，如果用DNN,RNN,BP神经网络，不能捕捉图像得局部信息。
• 图像得维度很大，输入就很大（要将图片拉平），这样如果做全连接的话，参数就会很多，下面我们看一个例子：

• 图像维度5x5
  第一层隐含层神经元个数 9
  输入：25
  输出 ：9
  参数：25 x 9

第二个问题：卷积的作用目的

• 卷积的目的还是作为特征的提取，做了卷积以后，如果做分类的任务，同样要加上全连接层，在进行激活，或者softmax做分类。

2.1、卷积的过程

卷积神经网络通DNN神经网络一样，也分为，输入层，输出层，和卷积层三部分。
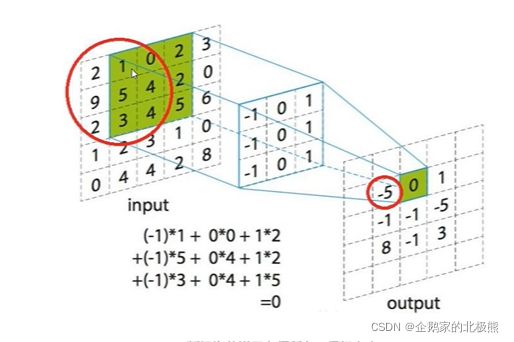
不同的是，这里的卷积层用的是卷积核来做卷积，不再是神经元。如下图：

在这里，你可以把卷积核看成是一个窗口，拿着这个“窗口”去扫描图片，扫描到的区域称之为感受野，这样的操作，就保证了模型可以考虑的图像得局部特征。

卷积的输出结果：
卷积核的每一个值，与对应感受野的值相乘，之后左右的结果相加。有偏置项的加上偏置项，在做一个激活函数进行激活，作为输出结果（上图中的例子没有做激活）

那么此时，一个卷积核的大小，就是对应参数的个数。

同样是上边的例子，我们看一下利用卷积来做的参数

图像维度 5x5
输出为3x3 = 9
卷积核大小 ：3x3
参数的个数 = 9

很明显，在兼顾了局部特征的前提下，参数个数大大降低。

2、卷积的参数

2.1、Padding填充

在Tensorflow中padding有两种属性：

• valid，表示不需要padding操作
  • 假设输入大小为n*n,卷积核大小为f *f，此时输出大小为(n-f+1);
• same，表示输入和输出的大小相同
  • 假设padding的大小为p，此时为了保持输出和输入消息相同p =(f-1)/2，但是此时卷积核要是奇数大小。

2.2、Stride步长

stride是指卷积核在输入上移动时每次移动的距离，直接上图来说明。其中
按红框来移动的话stride = 1;按蓝色框来移动的话stride = 2。加入stride后，输出的计算有一些变化，假设输入大小为n*n，卷积核大小为ff， padding大小为p,stride大小为s,那么最后的输出大小为:

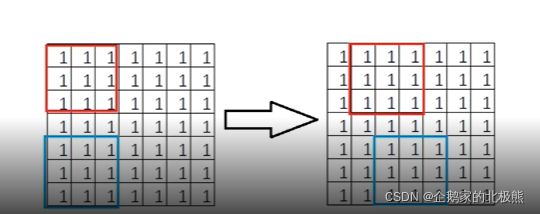
下面这个公式要熟记，有了这个公式，就可以计算应该Padding的大小，或者步长Stride的大小

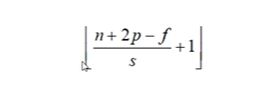
3、卷积核通道数的计算

卷积核有三种属性，分别为，大小，个数，通道数。
卷积核的个数不一定是一个，卷积核的通道数也不一定是一个。

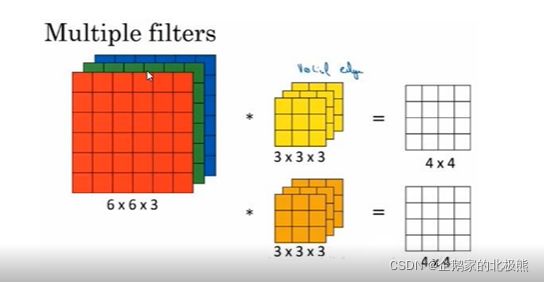
重点来了：这贯穿了整个卷积的计算和模型的优化

单个卷积核通道数 = 输入的通道数
卷积核的个数 = 输出通道数

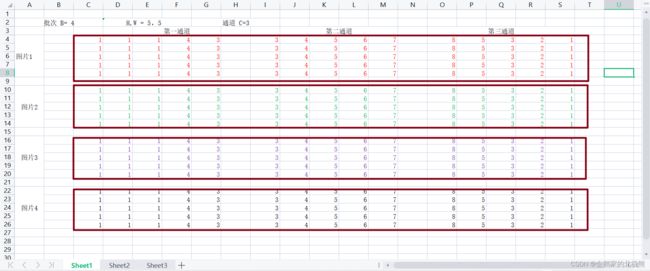
多通道卷积计算

每个通道做单通道卷积计算，不同通道结果相加
有偏置项的加上偏置项

多卷积核输出计算：拼接

每个卷积核做单个卷积核计算，多个卷积核的运算结果片接在一起，记得是拼接
拼接就说明，有多少个卷积核，输出就有多少通道。

这三个知识点很重要，后期产生的新模型的理解离不开这三个知识。
下面这个动图网址可以很好的帮助你理解多核多通道卷积的计算：http://cs231n.github.io/assets/conv-demo/index.html

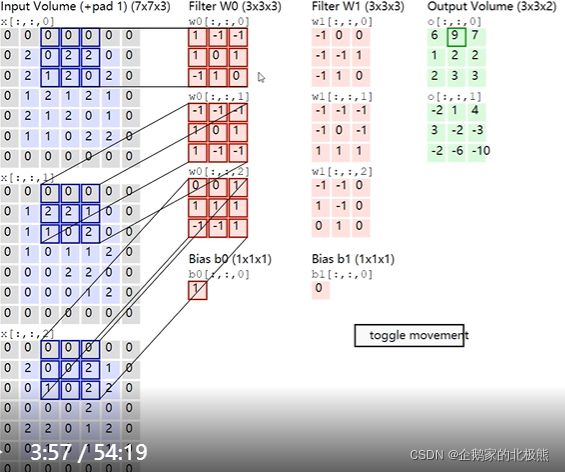
4、池化层

卷积网络中，除了卷积层以外，还有池化曾和归一化层。我们先来看一下池化层。池化层有最大值池化max-pooling,mean-pooling，自适应池化等。

做池化的目的是，对图片进行压缩，减少特征层大小
池化层同样具有步长和尺寸
池化层是不能改变通道数的
池化层是没有参数的

4.1、max-pooling

池化层依然是在窗口中做计算，如下图：
取窗口中数据的最大值
步长为2，大小2x2

4.2、mean-pooling

池化层依然是在窗口中做计算，如下图：
对窗口中的数据求平均值
步长为2，大小2x2

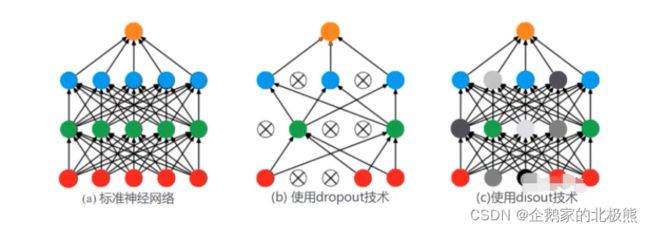
5、dropout和dropconnect、DropBlock、Disout提升模型精准率

前面我们提到在做卷积之后，要加上全连接层才可以做图像分类等任务，那么dropout一般在全连接层会用到
训练神经网络模型时，如果训练样本比较少，可以使用Dropout来一定程度减少过拟合。

重点：

dropout，等机制都只训练的时候才会用，预测的时候不能用。

1、dropout

为什么在在训练的时候才可以用，预测的时候不能用呢，因为作用机制：

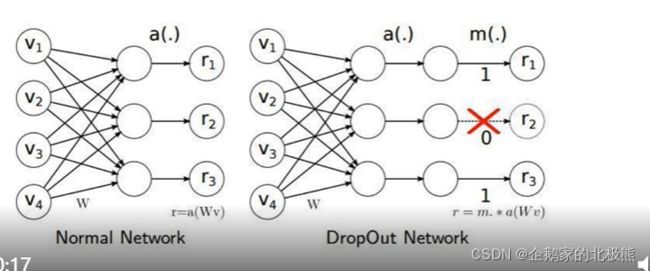
Dropout:随机抑制某一神经元作用（工作），使得输出为0
抑制的是神经元的输出

2、dropconnect

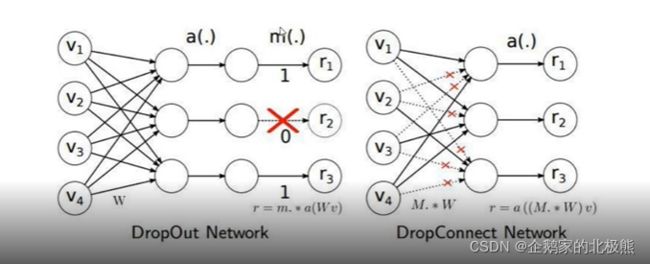
DropConnect：训练过程中，不是随机的将隐藏节点变为0，而是将节点中每个与其相连接的输入权值以1-p的概率编程0
抑制的是神经元的输入权值。

3、DropBlock
DropBlock一般在卷积中用

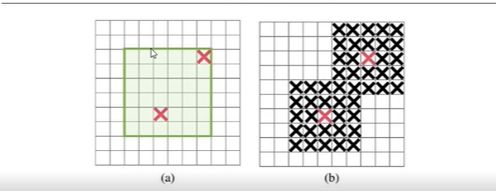
DropBlock和dropout的区别在于：

• dropout删除的是独立的随机单元（输出）
• DropBlock是从某层的feature map中删除相邻区域

Dropout的参数

block_size:控制要删除的块的大小
y:控制删除多少个激活单元

改进：

相比于所有feature channel共享一个DropBlock，每个 feature channel独立一个DropBlock更好

4、Disout
Disout是提出的新型替代方案，是一种通过研究“特征图扰动”来增强神经网络的泛化能力的方法。
作用机制（同样对比dropout看）：

简单来说：对输出特征记性扰动（加入噪音），而不是丢弃
具体实现：根据网络中间层的Rademacher复杂度（ERC），确定给定深度神经网络的误差上届。将扰动图引入特征图，来降低网络的Rademacher复杂度，从而提升泛化能力

6、不同激活函数大PK

激活函数的作用是做一和非线性的映射，在反向传播的过程中，根据激活函数的导数来更新权重。

6.1、sigmoid函数

作用机制：

将所有数据映射到（0,1）之间，很好的表达了神经元的激活与未激活的状态，适合二分类。

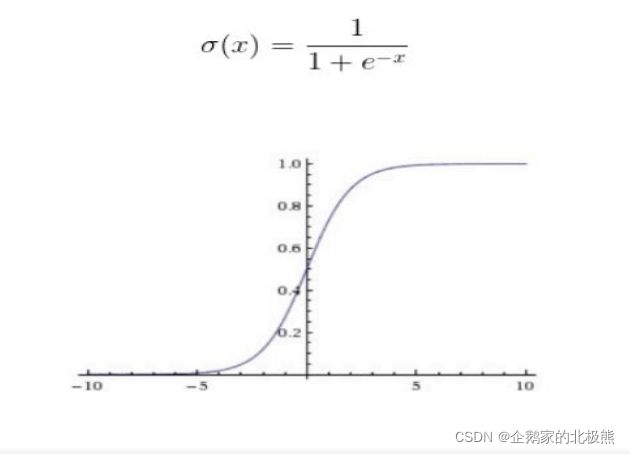
缺点：
sigmoid容易饱和，到那个输入非常大或者非常小的时候，函数曲线非常平坦，如上图所示，梯度非常接近于0，
在反向传播中，我们需要用sigmoid的导数来更新权重，如果导数基本为0，会导致权重没有什么更新，造成梯度弥散（梯度消失）。

与梯度消失相对应的时梯度暴涨，即梯度很大，这个时候要进行梯度裁剪。来解决。

6.2、tanh函数

作用机制：
tanh是在sigmoid基础上进行改进，将压缩范围调整到（-1.1）。

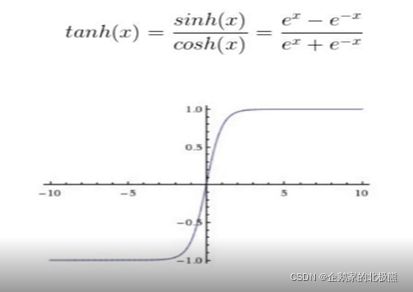
缺点：
任然存在梯度弥散问题

6.3、relu函数

作用机制：
relu函数是是目前比较主流的激活函数，多用于图像模型，他的公式简单，输入小于零的时候为0，输入大于零的时候为本身。

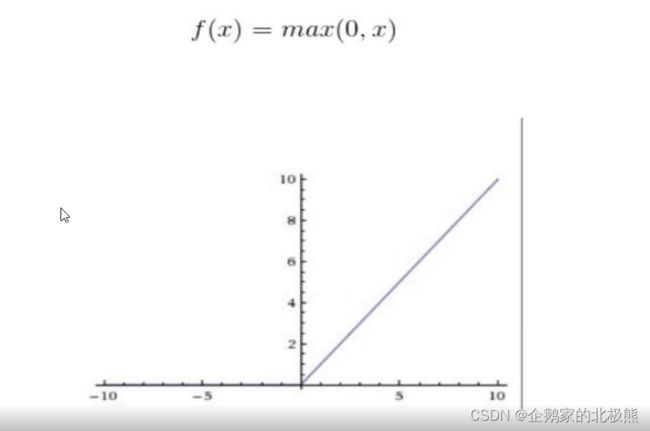
缺点：
当值为负数（权重为负数）的时候，直接置为0了。

6.4、Relu6函数

作用机制：
多Relu做了一个限制，限制最大输出值为6

**应用场景（目的）：**用在移动端设备的float16（float16这种低精度不能很好的描述大的数值范围）的低精度场景。

函数：

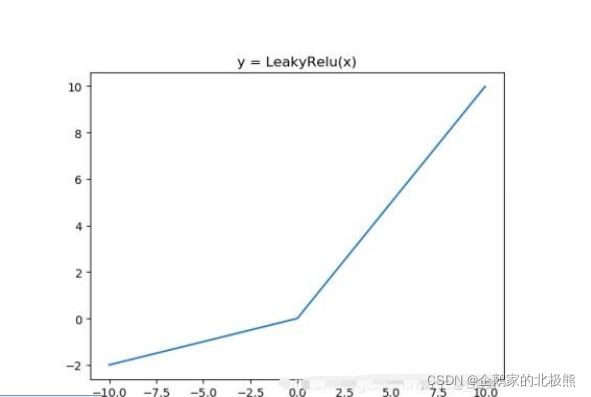
6.5、Leaky ReLU & PReLU

这两个函数是分段函数

作用机制：
在Relu上做的改进，当值为负数的时候，加上一个为a的斜率（乘a）
a一般取值0.25
a也可以作为学习参数参与到网络的训练中去。

表达式和导数公式：

6.6、ELU函数

作用机制：
改进Relu函数，使得在值为负数的时候有一定的输出，而这部分的输出还具有一定的抗干扰能力

缺点：
还是具有梯度饱和和知乎运算问题
公式：

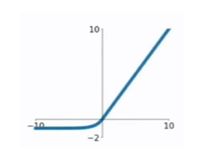
6.7、SELU函数

表达式：

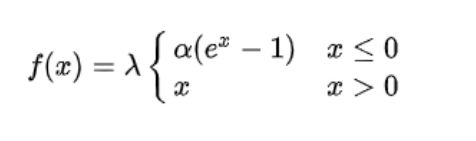
作用机制：自我标准化
当其中参数取值为
时，在网络权重服从正态分布的情况下，各层输出的分布会向标准正态分布靠拢。

优点:
避免梯度消失和爆照问题。让结构简单的前馈盛景网络获得甚至超越state - of - the - art的性能

6.8、Swish函数

表达式：

b是个常数或者可以训练的参数

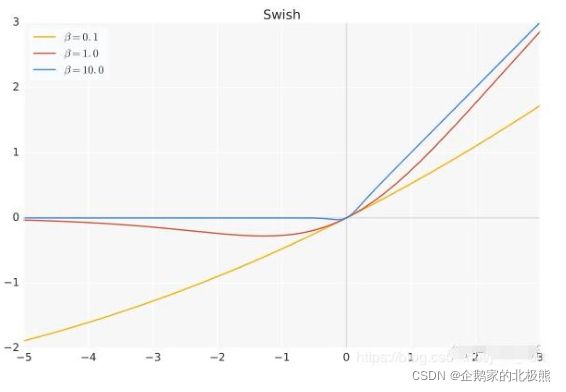
Swish特点
无上界，有下界，平滑，非单调
Swish在深层模型上优于Relu（也不一定，还是看数据集）

还有很多，不写了，有的时候就是试验，那个好用哪个。

7、卷积后的全连接层

全连接层在整个卷积的过程中起到的是“分类器”的作用，全连接的核心操作就是矩阵向量乘积 y = Wx

值得注意的是，在进入全连接层之前要把卷积的结果进行拉平。

8、深度学习的归一化层

在网络的每一层输入的时候，往往要加入归一化层，先做一个归一化处理，在进入网络的下一层。归一化层也属于网络的一层：
基本流程：
卷积————>归一化————>激活————>池化

做归一化必不可少的是求两个值：

• 平均值
• 方差

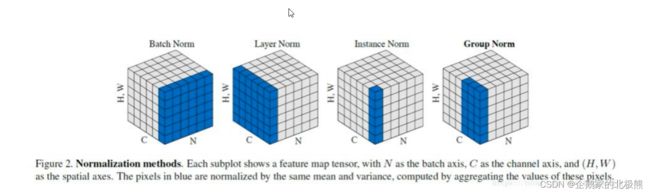
那么这四种归一化的不同 就在于在哪个维度上求这两个值。根据上边的图我们举个例子

现在假设：
训练数据的形状 【B,C,W,H】
B：代表一个批次的图片数量
C：代表通道数
W,H：代表图片的维度

一个批次数据形式如下：

8.1、Batch Normalization(BN)批归一化

对于上面的例子，BN即对这些值做归一化：

具体操作：

在训练神经网络时，同样学习归一化中的两个参数。

加入BN层的优点：

• 梯度传递更加顺畅，加速收敛
• 不容易导致神经元饱和，防止梯度消失，保证模型收敛（梯度弥散，梯度爆炸）
• 但是最好不要使用rlue激活函数，因为归一化以后，数据满足正太分布，在0~1之间波动，使用sigmiod，tanch更好
• 学习率可以设置的大一点
• 对于初始值的依赖更少

缺点：

• 如果网络层比较深，加入BN层，可能会导致模型训练速度很慢
• 受批次大小影响
• BN层慎用

均值和方差的传递：

上一批次的归一化操作，得出一个用于归一化的均值和方差值
当前次进来时，先计算当前批次的均值，方差u2，再上一批次得到的均值和方差同样进行传递下来，传递的方式是以一定的比例进行传递，比如上一批次得到的是u1，那么当前批次归一化值等于 a x u1 +u2
训练模型结束后保存最后批次的归一化结果，用于新数据做归一化操作的均值和方差。

import numpy as np
arr = np.arange(24).reshape(2,3,2,2)#B,C,H,W
def BN(X,gamma,beta):
    arr = X
    eps = 1e-5
    arr_m_ln = np.mean(arr,axis=(0,2,3),keepdims=True)
    arr_v_ln = np.var(arr, axis=(0,2,3), keepdims=True)
    x_normalized = (arr - arr_m_ln) / np.sqrt(arr_v_ln + eps)  # 层归一化
    result = gamma * x_normalized + beta

8.2、Group Normalization(GN)组归一化

这个要与LN对着看，LN是所有通道，GN是分组后一个组中的通道，这里我们假设分成两组

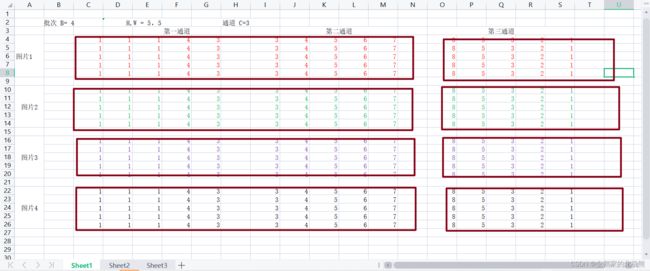
用在分组卷积上
主要是针对Batch Normalization对小batchsize效果差，GN将channel方向分group，然后每个group内做归一化，算(C//G)Hw的均值，这样与batchsize无关，不受其约束。

def GN(X,gamma,beta):
    arr2 = X.reshape(2,3,1,2,2)#B,C,H,W——>B表示不同的批次，即不同的样本
    #LN层归一化
    eps = 1e-5
    arr_m_ln = np.mean(arr2,axis=(2,3,4),keepdims=True)#让不同的样本做归一化
    arr_v_ln = np.var(arr2,axis=(2,3,4),keepdims=True)#求方差
    x_normalized = (arr2 - arr_m_ln)/np.sqrt(arr_v_ln + eps)#层归一化
    result = gamma * x_normalized + beta#gamma,beta是要学习的参数
    print('我们的数组是：\n',arr2)
    print('arr_m_ln:\n',arr_m_ln)

8.3、Layer Normalization(LN)层归一化

层归一化，对于对于上面的BN归一化，他是对批次的大小比较敏感，由于每次计算的均值和方差都在同一个批次内，则计算的均值和方差不足以代表整个数据的分布，这也可以看做是BN归一化的一个缺点。

• LN中同层神经元的输入具有相同的均值和方差，不同的样本具有不同的均值和方差。
• BN中则针对不同神经元的输入计算均值和方差，同batch中拥有相同的均值和方差
• LN用于RNN效果比较明显，但是在CNN上不如BN
  

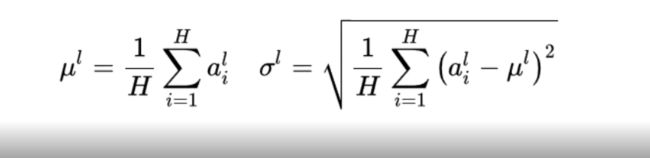
def LN(X,gamma,beta):

    arr = X#B,C,H,W——>B表示不同的批次，即不同的样本
    #LN层归一化
    eps = 1e-5
    arr_m_ln = np.mean(arr,axis=(1,2,3),keepdims=True)#让不同的样本做归一化
    arr_v_ln = np.var(arr,axis=(1,2,3),keepdims=True)#求方差
    x_normalized = (arr - arr_m_ln)/np.sqrt(arr_v_ln + eps)#层归一化
    result = gamma * x_normalized + beta#gamma,beta是要学习的参数
    print('我们的数组是：\n',arr)
    print('arr_m_ln:\n',arr_m_ln)

8.4、Instance Normalization(IN)归一化

图像风格华中，生成结果，主要依赖于某个图像的图像实例，因而要对H,W做归一化操作

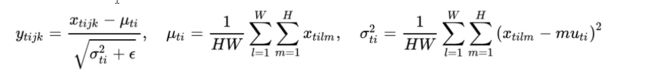
优点：

• 加速模型收敛
• 保重每个图像实例之间的独立性

def IN(X,gamma,beta):
    arr3 = X  # B,C,H,W——>B表示不同的批次，即不同的样本
    # LN层归一化
    eps = 1e-5
    arr_m_ln = np.mean(arr3, axis=(2, 3), keepdims=True)  # 让不同的样本做归一化
    arr_v_ln = np.var(arr3, axis=(2, 3), keepdims=True)  # 求方差
    x_normalized = (arr3 - arr_m_ln) / np.sqrt(arr_v_ln + eps)  # 层归一化
    result = gamma * x_normalized + beta  # gamma,beta是要学习的参数
    print('我们的数组是：\n', arr3)
    print('arr_m_ln:\n', arr_m_ln)

重点在BN层的原理一节优缺点，面试常问

9、参数初始化操作

神经网络的各种层都要学习参数，开始的时候要初始化参数，太大太小都不好。

• 参数过小：会导致神经元输入过小，经过多层之后，信号慢慢消失，参数过小还会使得sigmoid型函数丢失非线性能力（参考sigmoid曲线，在靠近0的位置，趋近于线性，）。
• 参数过大，导致输入状态过大，同样对于sigmoid型函数，激活值变得饱和，导致梯度接近于0.

9.1、random initialization 随机初始化

随机初始化的弊端：

• 一旦随机分布不当，会导致网络优化陷入困境（局部最优解）。从而影响模型收敛速度，甚至不收敛。

9.2、Xavier初始化

Xavier initialization可以解决上面的问题! Xavier初始化的基本思想是保持输入和输出的方差一致，这样就避免了所有输出值都趋向于0。tanh激活函数下，输出值依然保持着良好的分布，那么ReLU神经元。

9.3、其他初始化方法

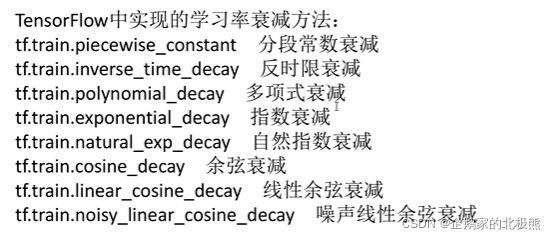
10、学习率

学习率（Learning rate）,作为监督学习以及深度学习中的超参数：

• 决定着目标函数能否收敛到局部的最小值
• 决定着收敛到最小值的速度
• 合适的学习率可以兼顾以上两点
  在机器学习中学习率我们是设定的固定超参值，实际上学习lv也是可以随着训练变化的。
  对比大小学习率的优缺点：
  
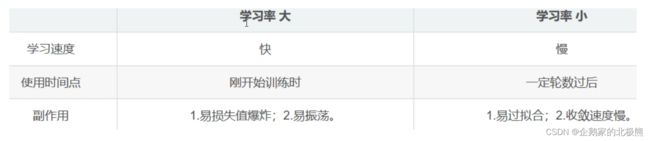
  经过试验得到：

刚开始训练时：学习率以0.1~~0.001为宜
一定轮次后：逐渐减缓
接近训练结束：学习率的衰减应该在100倍以上

另外，除了修改激活函数，修改学习率也是一种优化模型的方法。

11、数据增强必不可少

对于图像模型，数据增强常用的两种方式

• 翻转
• 裁剪

数据增强是从数据本身提升模型效果。

12、优化器

12.1、SGD+动量

在训练的时候我们更新梯度的时候会用到优化器，这里的优化器我们用SGD+动量的形式
普通的SGD方式；

theat = theta - lr*grad

SGD+动量：在grad上加上一个记忆参数，用来传递上一次grad的信息

初始化：
v0
monentum = 0.9 一般都设置成0.9
theta0
第一次迭代：
v1 = v0+monentumgrade
theta1 = theta0 - lrv1
第二次迭代：
v2 = v2+monentumgrade
theta2 = theta1 - lrv2

是这样迭代更新的

12.1、Adam+动量

后面再更新