遗传算法求解一元函数最大值||python

最近学习了人工智能这门课，就尝试着编写了一个小程序；

话不多说直接上（具体原理就自行百度吧）

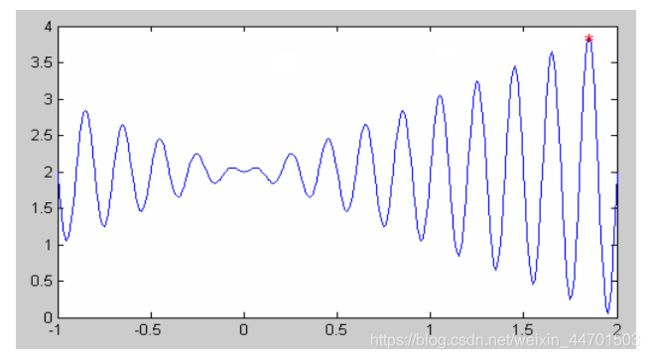
例：求一元函数的最大值   其中 

# -*- coding: utf-8 -*-
"""
Created on Tue Jun 03 16:22:15 2021

@author: Overcoming
"""
'''求一元函数的最大值
f (x) = xsin(10  x) + 2.0 x[−1,2]
'''
import random
from math import *
import matplotlib.pyplot as plt


#没写精英解保持容易陷入局部最优？ 和种群数量有关系


N = 200
Pcross = 0.75
Pchange = 0.05

def ori (N):
    #产生初始种群
    
    X = []
    JY1 = []
    #JY2 = []
    i = 0
    while i>d&1 for d in range(22)][::-1] #22位数以列表存储
        #JY2.append(jy2)
        x = (-1.0 + x*(2-(-1))/(2**22 - 1)) #原始坐标上对应的x取值
        X.append(x)
        i+=1
    return X,JY1


def Y_v(X):
    #计算个体适应度
    
    Y = []
    for i in range (0,len(X)):
        y = X[i]*sin(10*pi * X[i]) + 2.0 #适应度
        Y.append(y)
    return Y

def cross(JY1,X,N):
    #单点交叉产生下一代
    
    while len(JY1)< 2*N:
        p = random.uniform(0,1) # 随机产生概率
        if p <= Pcross:  #75%概率交叉
            i = random.randint(0,N-1)
            j = random.randint(0,N-1)
            k = random.randint(0,22)
            a = JY1[i][:k] + JY1[j][k:]
            x = int(a,2)  #二进制转为十进制
            x = (-1.0 + x*(2-(-1))/(2**22 - 1))
            X.append(x)
            JY1.append(a)
            
            b = JY1[j][:k] + JY1[i][k:]
            x = int(b,2)  #二进制转为十进制
            x = (-1.0 + x*(2-(-1))/(2**22 - 1))
            X.append(x)
            JY1.append(b)
        else:
            i = random.randint(0,N-1)
            a = JY1[i]
            x = int(a,2)  #二进制转为十进制
            x = (-1.0 + x*(2-(-1))/(2**22 - 1))
            X.append(x)
            JY1.append(a)
       
            
            
    return X,JY1

def cg (JY1,X):
    #突变
    
    N = len(JY1)
    p = random.uniform(0,1) #随机产生概率
    if p <= Pchange:
        i = random.randint(0,N-1)
        k = random.randint(0,21)
        x = int((X[i]+1.0)*(2*22-1)/(2-(-1))) #将实际x值映射到编码前十进制数
        JY2 = [x>>d&1 for d in range(22)][::-1] #22位数以列表存储
        JY2[k] = -JY2[k]+1 #该点突变
        jy2 = [str(i) for i in JY2]
        JY1[k] = ''.join(jy2)
        x = int(JY1[k],2)
        X[k] = (-1.0 + x*(2-(-1))/(2**22 - 1)) #算出对应值。
    
    return X,JY1    

    
def P (Y):
    # 计算个体被挑选概率
    N = len(Y)
    PS = []
    PC = []
    for i in range(0,N):
        ps = (Y[i]/sum(Y))  # 被选取概率
        PS.append(ps)
        pc = sum(PS[:i]) + ps #累计概率
        PC.append(pc)
    return PS,PC

def sel (PC,N):
    #轮盘赌挑选新个体
    l =[]
    k = len(l)
    while k < N:
        i = random.uniform(0,1)
        for j in range(0,len(PC)):
            if PC[j]>= i :
                l.append(j)
                break  #没加break要命。。。
        k = len(l) 
    return l

def diedai(X,JY1,N):
    T =[]
    Y_m = []
    Y_av = []
    X_m = []
    m = 0
    while m <200:
        m += 1
        [X,JY1] = cross(JY1,X,N)
        [X,JY1] = cg(JY1,X)
        Y=Y_v(X)
        [PS,PC] = P(Y)
        index_N = sel(PC,N)
        #print(len(index_N))
        X = [X[i] for i in index_N]
        JY1= [JY1[i] for i in index_N]
        Y=Y_v(X)
        T.append(m)
        max_index = Y.index(max(Y, key = abs))
        Xm = X[max_index]
        X_m.append(Xm)
        Ym = Y[max_index]
        Y_m.append(Ym)
        Yav = sum(Y)/len(Y)
        Y_av.append(Yav)
    print('第%d代'%m)
    return X,JY1,Y,Y_m,X_m,Y_av,T
    




[X,JY1] = ori(N)
[X,JY1,Y,Y_m,X_m,Y_av,T]=diedai(X,JY1,N)
#print('PS= '+ str(PS)+'\n')
#print('PC='+ str(PC) + '\n')
max_index = Y.index(max(Y, key = abs))
JY1m = JY1[max_index]
Xm = X[max_index]
Ym = Y[max_index]
print('最佳个体：')
print('JY1m = '+ JY1m)
print('Xm = '+ str(Xm))
print('Ym = '+ str(Ym))
fig, ax = plt.subplots()  #ax在这里定义。
plt.subplot(2,1,1)
plt.plot(T,Y_m,T,Y_av)
plt.title('The change with the ages')  
plt.legend(['Y_m','Y_av'])
plt.text(30, 2.8, "The final Y is "+str(Ym), size = 15, alpha = 0.5,color = 'b')
#plt.show()
plt.subplot(2,1,2)
plt.plot(T,X_m)
plt.legend('X_m')
plt.text(0.2, 0.2, "The final X is "+str(Xm), size = 15, alpha = 0.5,color = 'b',transform=ax.transAxes)
#上面text 用的是绝对位置
plt.show()

附上其中一次运行结果

代码写的实在垃圾常常陷入局部最优也不规范，希望大佬们多多指正。