动态规划算法讲解(小白也看得懂)

    在讲解题目之前，读者需要初步了解动态规划算法。动态规划只要运用到数学归纳法的思想，也就是可以通过子问题的解推出父问题的解，为了让读者能够进一步的理解我就举个例子吧。

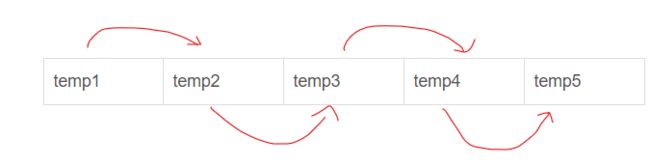
    下面为一个数组，该数组的长度为5。假设temp1的值已知，并且我们能同过temp 1推出temp2,通过temp2推出temp3,通过temp3推出temp4, 通过temp4推出temp5。我们就称此方法为数学归纳法。(一步步的先后推来得到最终答案) 

    由于数学归纳法特性，大多数读者可能都会采用递归的方法来解题，确实采用递归的方法会很方便，整体的代码看起来也会比较整洁。由于这里还未涉及到代码，所以读者可能很难发现解决此类问题用递归的弊端。所以在此我建议读者先观看我的上一篇文章,上篇文章会帮助你加快对下文代码的理解速度。

https://blog.csdn.net/Ostkakah/article/details/118160844?spm=1001.2014.3001.5502

    接下来我写的代码都会采用'备忘录'的思想和空间压缩的思想对代码进行优化。

    题目一：最长公共子序列(str1 = "abcde", str2 = "aceb",算法应输出3,因为最长公共子序列为"ace",它的长度为3)

    首先我们应该都会想到同时对两个字符串进行遍历，但遍历时又要添加一些条件是什么呢？

    因为要对两字符串同时遍历，所以我们可以创建一个二维数组，以列出所有情况。

str1\str2	null	b	a	b	c	d	e
null	0	0	0	0	0	0	0
a	0
c	0
e	0

    如上图所示，二维数组data[][8],null 为空字符串，空字符串于其他字符串求最长公共子序列时都为0，所有接下来

我们只要求出二维数组中未赋值的项再取最后一个值，就可以求出最终答案了。

  但未赋值项与已知项存在着什么关系呢？这算是一个难点，我们可以知道横纵序号代表的是指向对应字符串中的值。假设这两个值相等，我们就可以通过data[i-1][j-1]的值就可以求出data[i][j]的值。(i,j为遍历指针)因为两值相等，所以只要对data[i-1][j-1] + 1就是data[i][j]的值。这是第一种情况，当两个值不相等时我们就要另外考虑了，我们要分别求出data[i - 1][j]和data[i][j-1]的值，data[i - 1][j]代表str1[i -1]字符串和str2[j]间的最长公共子序列，data[i][j - 1]代表str1[i]字符串和str2[2]字符串的最长公共子序列。由于我们要求的时最公共长子序列 ,所以就取data[i - 1][j]和data[i][j-1]两者间较大的值，前面的情况中都至少有str1[i]或str2[j]存在于当前的最公共长子序列中，可能会有读者会问那str[i],str[j]都不在最长公共子序列的情况呢？

    其实已经包含在data[i - 1][j]和data[i][j - 1]中了，当两者都不存在时，在data[i -1][j]和data[i][j - 1]中求出的最长公共子序列不会包含str1[i]和str2[j]。

    所以我们已经考虑出了所有情况,为了方便读者的理解，我就用图来表示二维数组中项于项间的关系。

data[i - 1][j - 1](str1[i]和str2都存在于最长公共子序列的子问题情况)	data[i  - 1][j](str[j]存在于最长公共子序列的情况或str1[i]str2[j]都不存在图最长公共子序列的情况)
data[i][j  - 1](str[i]存在于最长公共子序列的情况或str1[i]str2[j]都不存在图最长公共子序列的情况)	data[i][j]

有了这些思路我们就可以写出代码：

#include
#include
#define M 255

int longest(char *,char *);

int main()
{
	char str1[M], str2[M];
	gets(str1);
	gets(str2);
	 
	printf("最长公共子序列为: %d", longest(str1, str2));
	return 0;
}

int longest(char *str1, char *str2)
{
	int str1Size, str2Size, i, j;
	str1Size = strlen(str1);
	str2Size = strlen(str2);
	int data[str1Size + 1][str2Size + 1];
	//初始化
	 for(i = 0; i <= str1Size; i++){
	 	for(j = 0; j <= str2Size; j++){
	 		if(i==0||j==0){
	 			data[i][j] = 0;
			 }
		 }
	 }
	 //主循环,从未赋值项开始赋值 
	 for(i = 1; i <= str1Size; i++){
	 	for(j = 1; j<=str2Size; j++){
	 		if(str1[i - 1] == str2[j - 1]){
	 			data[i][j] = data[i - 1][j - 1] + 1;
			 }else{//不相等的情况 
			 	data[i][j] = (data[i - 1][j] >= data[i][j - 1]) ? data[i - 1][j] : data[i][j - 1];
			 }
		 }
	 }
	 return data[str1Size][str2Size]; 
}

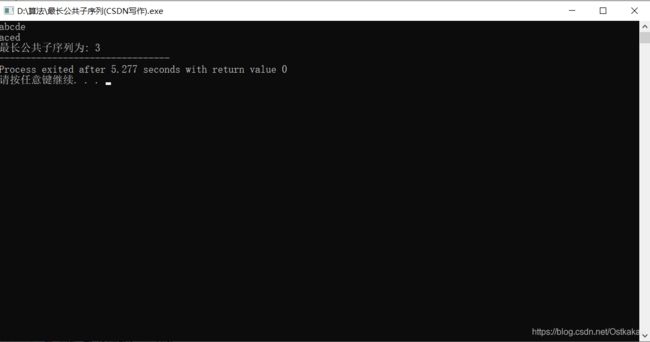
其运行结果为：

    这里有个小技巧，我推荐读者可以先采用递归的方法来解题，因为通过递归的方法我们可以快速的理清解题的思路，便于后期的代码优化,后期的代码优化无非就是采用'备忘录'的思想具体，这题我采用二维数组作为'备忘录'。

    以下是递归的方法，便于读者理解。

int longest(int str1Size, int str2Size, char *str1, char *str2)//str1Size为str1的长度-1, str2Size为str2的长度-1;
{
	if(str1Size<0||str2Size<0){
		return 0;
	}else{
		if(str1[str1Size] == str2[str2Size]){
			return longest(str1Size - 1, str2Size - 1, str1, str2);
		}else{
			int temp1 = longest(str1size - 1, str2size, str1, str2), temp2 = longest(str1size, str2size - 1, str1, str2);
			return (temp1 >= temp2) ? temp1 : temp2;
		}
	}
}

  我想通过上面这道题，读者应该对动态规划的理解有了很大的提高，所以接下来我们再来试一道题。

   题目二：最长回文子序列(s = "aecda"，算法返回3，因为最长回文子序列str为"aca")

   此题重点讲代码的优化思路。

  首先想一想递归的思路(可以在自己的脑子里构造一个二维数组)。

设i为从左向右走的指针，j为从右向左走的指针，结束条件应该是i>j,并且结束的结果应该为1，因为一个字母本身就是一个回文。接下来我们就开始考虑子问题推出父问题的关系式，我们先来判断一下s[i]和s[j]是否相等，如果相等我们就考虑第一种情况，也就是去求s[i + 1]和s[j - 1]的最长回文子序列数，将此子回文数+2就是str[i]和str[j]对应的子回文数。第二种情况为s[i]！=s[j],也就是求出s[i + 1]，str[j]和s[i][j - 1]中较大的回文子序列数, 该情况包含了只有一个字母存在于str和两字母都不存在于str的两种情况。

递归代码为:

#include
#include
#define Max 255

int longest(int, int, char *);

int main()
{
	char s[Max];
	gets(s);
	printf("最长回文子序列的个数为 ：%d", longest(0, strlen(s), s));
	return 0;
}

int longest(int i, int j, char *s)
{
	if(i >= j){
		return (i > j) ? 0 : 1;
	}else{
		if(s[i] == s[j]){
			return longest(i + 1, j - 1, s) + 2;
		}else{
			int temp1 = longest(i + 1, j, s), temp2 = longest(i, j - 1, s);
			return (temp1 >= temp2) ? temp1 :temp2;
		}
	}
}

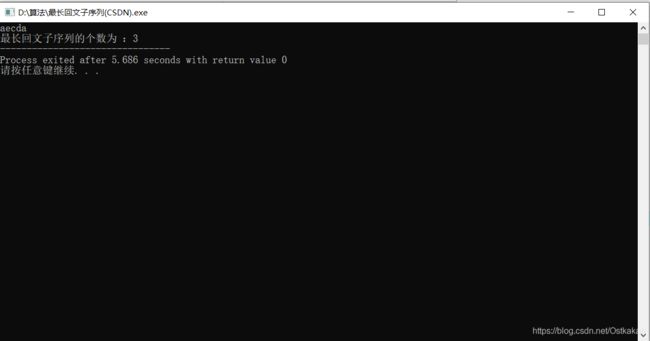
运行结果为：

代码优化一：备忘录法

接下来我们来优化代码也就是使用'备忘录'思想实现,我们需要创建一个二维数组。

下图为初始0状态：

1
0	1
0	0	1
0	0	0	1
0	0	0	0	1

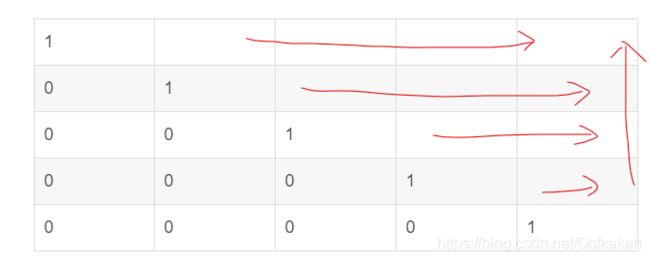
为了保证数据项的下，左，左下,都有值，我们需要采用逆遍历。

逆遍历的遍历方向入下图：

最终的实现代码如下：

#include
#include
#define Max 255

int longest(char *);

int main()
{
	char s[Max];
	gets(s);
	printf("最长回文子序列数为 ：%d", longest(s));
	return 0;
}

int longest(char * s)
{
	int size = strlen(s), i ,j;
	int data[size][size];
	//初始化,当i>j时说明不存在回文所以初始化为0,当i==j时说明回文就为字母本身所以初始化为1; 
	for(i = 0;i < size; i++){
		for(j = 0; j <= i; j++){
			data[i][j] = (i == j) ? 1 : 0;
		}
	}
	//主循环;
	for(i = size - 2; i >= 0; i--){
		for(j = i + 1; j < size; j++){//逆遍历; 
			if(s[i] == s[j]){
				data[i][j] = data[i + 1][j - 1] + 2;
			}else{
				data[i][j] = (data[i][j - 1] >= data[i + 1][j]) ? data[i][j - 1] : data[i + 1][j]; 
			}
		}
	}
	return data[0][size - 1]; 
}

    在此我们就实现里代码的优化任务，这里读者思考一个问题：这是最优解法吗？答案显然是否。

我们可以计算出空间复杂度为O(n^2)，我们通过观察不难发现，逆遍历完的数据除了在逆遍历行的下一行(i + 1行)有用， 其他已遍历完的数据已经没用了，还用空间去储存它们实在是浪费，所以我们能否用一维数组来代替二维数组，这就涉及到空间压缩的问题。

代码优化二：状态压缩法(适合进阶，小白可跳过)

此方法难点在于如何用一维数组(number[strlen(s)])来表示题目的两种情况，因为逆遍历时每行开始遍历的位置对应的data[i][j -1](左)为1，所以我们要将二维数的值全部初始化为1。data[i + 1][j](下)的值其实就是开始遍历 i 行时的初始值也就是i + 1行对应的数值，那data[i + 1][j - 1]的值怎么表示呢？其实也是比较容易的，我们需要一个临时变量temp,用它来记录number[i -1]的初始值(i + 1行对应number[i - 1]的值)，最终我们就可以写出代码了。

对应代码如下：

#include
#include
#define Max 255

int longest(char *);

int main()
{
	char s[Max];
	gets(s);
	printf("最长回文子序列的个数为：%d", longest(s));
	return 0;
}

int longest(char *s)
{
	int size = strlen(s), i, j;
	int number[size];
	//初始化;
	for(i = 0;i < size; i++){
		number[i] = 1;
	}
	//主循环(在脑子里构造一个二维数组);
	for(i = size - 2; i >= 0; i--){
		int pre = 0;//遍历每行的首项对应的data[i + 1][j - 1]都为 0,所以初始化为 0,且为'左下'; 
		for(j = i + 1; j < size; j++){
			int temp = number[i];
			if(s[i] == s[j]){
				number[j] = pre + 2;
			}else{
				//初始number[j]的值对应为'下' ,number[j - 1]为'左'; 
				number[j] = (number[j] >= number[j - 1]) ? number[j] : number[j - 1];
			}
			pre = temp;//将项一项对应的'左下'的值赋给pre; 
		}
	}
	return number[size - 1];//返回data[0][j]对应的值; 
}

运行结果为：

    此代码的空间复杂度为O(n)，减少内存的开销的效果非常好，但是此代码还是存在着可读性差的缺点,且仅能用在特殊的遍历顺序上， 所以空间压缩有好有坏，最终还是要看读者的选择。

---

总结

1.动态规划的解法框架为：

if(最小子问题的条件){

        //最小子问题子问题的解；
}else{

        if(两指针指向的值相等){

                //减少范围求子问题；

        }else{

                //两指针指向的值不相等

                //减少范围求子问题；

        }

}

2. 动态规划算法实现的对应代码的优化方向有涉及到 '备忘录'思想,  '空间压缩'思想。