吴恩达机器学习课程-第二周
1.多变量线性回归
1.1 多维特征
在第一周的学习中探讨了单变量的回归模型,现在对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为 ( x 1 , x 2 , . . . x n ) (x_1,x_2,...x_n) (x1,x2,...xn)。 x j ( i ) x^{(i)}_j xj(i)代表特征矩阵中第 i i i行的第 j j j个特征,也就是第 i i i个训练实例的第 j j j个特征
综上, h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxn,其中 x 0 = 1 x_0=1 x0=1
1.2 多变量梯度下降
重复执行下面公式直至收敛:需要同时更新 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、… θ n \theta_n θn(第一项中的 x 0 = 1 x_0=1 x0=1,所以在第一周中省略了)
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) ) x 0 ( i ) \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))x^{(i)}_0 θ0:=θ0−αm1∑i=1m(hθ(x(i)−y(i)))x0(i)
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) ) x 1 ( i ) \theta_1:=\theta_1-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))x^{(i)}_1 θ1:=θ1−αm1∑i=1m(hθ(x(i)−y(i)))x1(i)
θ 2 : = θ 2 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) ) x 2 ( i ) \theta_2:=\theta_2-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))x^{(i)}_2 θ2:=θ2−αm1∑i=1m(hθ(x(i)−y(i)))x2(i)
…
θ n : = θ n − α 1 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) ) x n ( i ) \theta_n:=\theta_n-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))x^{(i)}_n θn:=θn−αm1∑i=1m(hθ(x(i)−y(i)))xn(i)
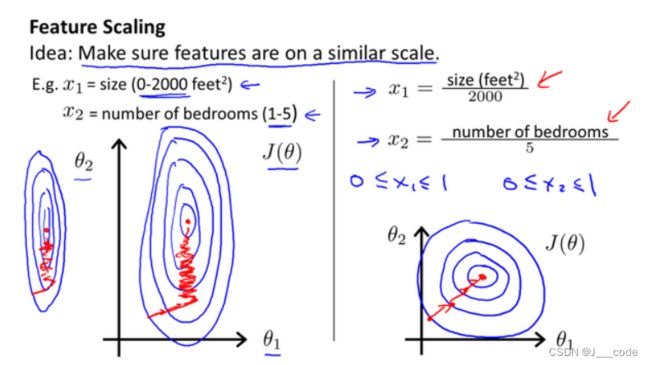
1.3 梯度下降法-特征缩放
在面对多维特征问题的时候,要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。以房价问题为例,如果使用两个特征:房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图(左边图像),看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛:
特征缩放最简单的方式就是 x n = x n − μ n s n x_n=\frac{x_n-\mu_n}{s_n} xn=snxn−μn,其中 μ n \mu_n μn是平均值, s n s_n sn是标准差
1.4 梯度下降法-学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛:
除此之外,还可以依靠自动收敛测试,即如果每一次迭代 J ( θ ) J(\theta) J(θ)下降的值小于某个值 δ \delta δ(一般为 1 0 − 3 10^{-3} 10−3),就认为收敛。但是该方式的缺点在于选取一个合适的 δ \delta δ比较困难
如果 J ( θ ) J(\theta) J(θ)随着迭代次数在不断增加,则可能是因为学习率 α \alpha α过大,导致在 J ( θ ) J(\theta) J(θ)的局部最小值附近不停摆动并且不断增大,所以需要减少 α \alpha α。当然 α \alpha α太小会导致收敛速度过慢
可以尝试以下学习率: α = 0.01 , 0.03 , 0.1 , 0.3 , . . . \alpha=0.01,0.03,0.1,0.3,... α=0.01,0.03,0.1,0.3,...
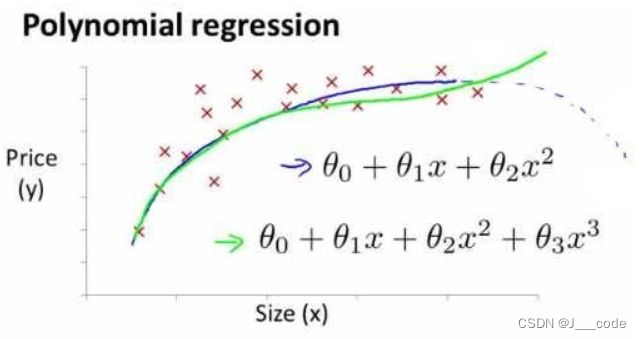
1.5 特征和多项式回归
假设在房价预测问题上, h ( θ ) = θ 0 + θ 1 × f r o n t a g e + θ 2 × d e p t h h(\theta)=\theta_0+\theta_1×frontage+\theta_2×depth h(θ)=θ0+θ1×frontage+θ2×depth,其中 x 1 = f r o n t a g e x_1=frontage x1=frontage表示临街宽度, x 2 = d e p t h x_2=depth x2=depth表示纵向深度,但实际上影响房价的元素很大概率是面积 x 3 = f r o n t a g e × d e p t h = a r e a x_3=frontage×depth=area x3=frontage×depth=area。所以为了使用数据,可能需要多项式模型,下图是一个特征的多项式模型图像:
如果采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要,因为使用到平方、立方等
2.正规方程
目前使用的都是梯度下降算法,需要经过多次迭代才会获得最优参数。但是对于某些线性回归问题,正规方程方法是更好的解决方案,它可以一次性得到最优参数:
①假设 J ( θ ) = a θ 2 + b θ + c J(\theta)=a\theta^2+b\theta+c J(θ)=aθ2+bθ+c,其中参数 θ \theta θ为实数时(即只有一个特征),正规方程通过 d d θ J ( θ ) = 0 \frac{d}{d\theta}J(\theta)=0 dθdJ(θ)=0求出 θ \theta θ
②假设 J ( θ 0 , θ 1 , . . , θ m ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1,..,\theta_m)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1,..,θm)=2m1∑i=1m(hθ(x(i))−y(i))2,其中参数 θ \theta θ为 n + 1 n+1 n+1维的向量时,正规方程通过 θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy求出 θ \theta θ,其中 X X X为训练集的特征矩阵, y y y为训练集结果向量(当然也可以①一样 d d θ j J ( θ ) = 0 \frac{d}{d\theta_j}J(\theta)=0 dθjdJ(θ)=0逐个求出 θ j \theta_j θj)
对于不可逆的矩阵,即特征之间存在联系(如不同单位的尺寸特征这样在数值上存在联系的特征)或者特征数大于训练集数,正规方程无法使用,需要采用到正则化进行处理
综上梯度下降和正规方程的区别如下:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要学习率 |
| 可能需要对特征进行缩放 | 一次性得到最优参数,不需要缩放 |
| 需要多次迭代 | 一次运算 |
| 特征数目n较大时也适用 | 特征数n较大时运算代价增加(矩阵逆的时间复杂度为 O ( n 3 ) O(n^3) O(n3)) |
| 适用于各种类型的模型 | 只适用线性模型,不使用于逻辑回归等模型 |
注意:可以通过判别决策边界是否为直线判断模型是否为线性模型,不能直接认定 y = 1 1 + a ⋅ e b + c ⋅ x y=\frac{1}{1+a·e^{b+c·x}} y=1+a⋅eb+c⋅x1就不是线性模型(参数 x x x只受一个系数 c c c的影响)
2.1 正规方程推导
下图中的 J ( θ ) J(\theta) J(θ)是由原来向量形式 J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2转换为矩阵形式 J ( θ ) = 1 2 ( X θ − y ) J(\theta)=\frac{1}{2}(X\theta-y) J(θ)=21(Xθ−y),其中 X X X为 m m m行 n n n列的矩阵, θ \theta θ为 n n n行1列的矩阵, y y y为 m m m行1列的矩阵( m m m为样本数, n n n为特征数)
3.参考
https://www.bilibili.com/video/BV164411b7dx?p=19-24
http://www.ai-start.com/ml2014/html/week2.html