PyTorch学习之autograd(自动求导)
autograd
1. 最常用的方法就是 torch.autograd.backward()
torch.autograd.backward(tensors,
grad_tensors=None,
retain_graph=None,
create_graph=False)作用:自动求取梯度
-
tensors:用于求导的张量,比如loss
-
retain_graph:保存计算图
-
create_graph:创建导数计算图,用于高阶求导
-
grad_tensors:多梯度权重
用例子来展示一下:假如求以下计算中y对w的偏导:
![]()
设
![]()
则有
![]()
那么
当我们取w = 2 ,x = 1时,结果等于7
用代码示例:
import torch
# y = (x+w)*(w+2)
# 创建叶子结点
w = torch.tensor([2.], requires_grad=True)
x = torch.tensor([1.], requires_grad=True)
a = torch.add(x,w)
b = torch.add(w,2)
y = torch.mul(a,b)
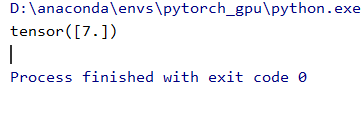
y.backward()
print(w.grad)运行结果也是和手动计算一样的
在backward之后程序会释放计算图,你可以尝试在y.backward()再添加一句y.backward()
y.backward()
y.backward()运行报错,可以看到提示说明在进行第二次backward时计算图已经被释放掉了
可以添加retain_graph = True保存计算图
y.backward(retain_graph=True)
y.backward()下面讲一下grad_tensors的使用方法
代码如下:
w = torch.tensor([2.],requires_grad=True)
x = torch.tensor([1.],requires_grad=True)
a = torch.add(x,w)
b = torch.add(w,2)
y0 = torch.mul(a,b) # y0 = (x+w)*(w+2) dy/dw = 7
y1 = torch.add(a,b) # y1 = (x+w)+(w+2) dy/dw = 2
loss = torch.cat([y0,y1],dim=0)
grad_tensors = torch.tensor([1.,2.]) # 梯度权重
loss.backward(gradient=grad_tensors) #将gradient传入torch.autograd.backward()中的grad_tensors
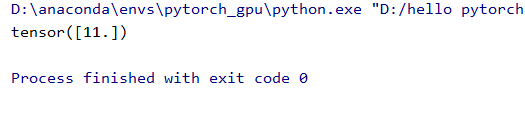
print(w.grad) #7*1+2*2 = 11相当于设置各个损失梯度的权重,最后将gradient传入torch.autograd.backward()中的grad_tensors
各行代码解释可以看下注释,运行也是得到了11的结果
2. torch.autograd.grad
作用:求取梯度
- outputs:用于求导的张量,比如loss
- inputs:需要梯度的张量
- create_graph:保存计算图
- grad_outputs:多梯度权重
torch.autograd.grad(outputs,
inputs,
grad_outputs=,
retain_graph=,
create_graph=False)用代码示例一下:![]()
求一阶导![]()
x = torch.tensor([3.],requires_grad=True)
y = torch.pow(x,2) #y = x**2
grad_1 = torch.autograd.grad(y,x,create_graph=True)#创建导数的计算图,否则无法进行高阶求导
print(grad_1)运行
求二阶导![]()
grad_2 = torch.autograd.grad(grad_1[0],x)# 注意grad_1是一个tuple,取第一个元素
print(grad_2)运行
关于autograd有几点需要注意:
- 梯度不会自动清零,下面用代码体现。
w = torch.tensor([2.], requires_grad=True)
x = torch.tensor([1.], requires_grad=True)
for i in range(2):
a = torch.add(x,w)
b = torch.add(w,2)
y = torch.mul(a,b)
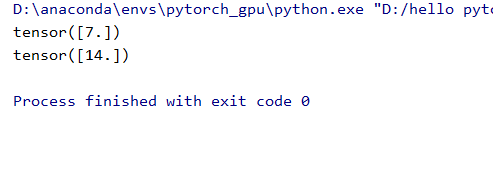
y.backward()
print(w.grad)运行结果如下,梯度会随着循环的次数累加。
当然可以通过代码(如下)实现梯度清零
w.grad.zero_()- 依赖于叶子结点的结点,require_grad默认为True
代码示例
w = torch.tensor([2.], requires_grad=True)
x = torch.tensor([1.], requires_grad=True)
a = torch.add(x,w)
b = torch.add(w,2)
y = torch.mul(a,b)
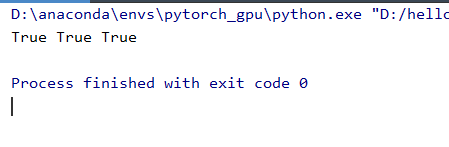
print(a.requires_grad,b.requires_grad,y.requires_grad)运行结果:
- 叶子结点不可以进行in-place操作(原位操作)
什么是原位操作?可以用代码解释一下
假设我们设定一个a,如果加上一个1向量,得到的地址和结果是什么样的呢?
a = torch.ones((1,))
print(id(a),a)
a = a + torch.ones((1,))
print(id(a),a)运行:
发现a的操作前后的地址不同,但是用原位操作进行加1试试
a += torch.ones((1,))
print(id(a),a)运行发现前后地址是一致的
但是在autograd中是不支持原位操作的,代码试一下:
w = torch.tensor([2.], requires_grad=True)
x = torch.tensor([1.], requires_grad=True)
a = torch.add(x,w)
b = torch.add(w,2)
y = torch.mul(a,b)
w.add_(1)
y.backward()
print(w.grad)
运行发现报错不能进行in-place操作
为什么不能进行原位操作呢?因为在正向传播时候,用到了叶子结点的数值,之后反向传播用到的叶子结点依然还是通过这个内存地址进行取值的,如果原位操作就会造成传播前后的数值不一致问题。