新冠疫情预测模型--逻辑斯蒂回归拟合、SEIR模型

  通过构建统计学模型、数学模型，或者利用机器学习、深度学习方法拟合疫情发展趋势，利用历史数据对未来的确诊病例等疫情形势进行预测，比如说，逻辑斯蒂生长曲线拟合数据，预测未来几天可能的发展趋势；或者利用时间序列模型构建预测模型；也可用LSTM构建预测模型，一种特殊的RNN网络。以上方法，除生长曲线外，其他模型，需要大量数据做训练，就目前情况看，数据量并不大，即使构建出模型，参考价值并不大，并没有与业务做融合，只是以数据理解数据。

  另外一个建模思路，可以从传统疾病传播模型（SIS、SIR、SEIR等），建立传染病模型，结合此次冠状病毒的传播特性，利用现有的样本数估计出一个大概的参数，建立适当的传染病数学模型，能较为精准的预估疫情的发展趋势，当然这是一个较为复杂且专业的问题。近日，由钟南山院士团队研究构建的「具有饱和发病率（其解释，任何传染病都具有饱和发病率，即不可能完全被消灭） SIQS 传染病模型」虽然被国外权威期刊退回，但研究成果还是符合国内疫情发展趋势。

  据有关学者介绍，SIQS传染病模型实际上是在传统SEIR模型基础上，加上两个干预因素，即国家的强力干预和春节后的回程高峰，另外，2020年2月28日，钟南山院士团队发表了一篇名为《公共卫生干预下COVID-19流行趋势的 SEIR和AI预测修正》，将2020年1月23日前后的人口迁移数据及最新的新冠肺炎流行病学数据整合到SEIR模型中生成流行曲线，同时，团队还利用人工智能技术，以2003年SARS数据为基础进行训练，从而更好地预测新冠疫情。研究团队还使用长短期记忆模型，预测新增感染数随时间的变化。对于基本训练数据集的处理，研究团队利用 2003年4-6 月SARS的病例统计，纳入COVID-19流行病学参数。从钟南山院士团队的研究成果来看，假设是一支纯技术团队，是无法作出解释性强、可信度高的预测模型，所以说数据建模不仅仅依靠的是技术工具，更多的是业务理论背景，模型不应该是冰冷的技术实现，更应该是有温度、有内涵的业务与技术的融合。

  因本人不具备传染病、医疗专业领域相关知识，从非专业角度，尝试利用Logistic生长曲线模拟泰安地区累计确诊病例数量，并试着简单叙述传统疾病传播模型-SEIR。
  （一）Logistic生长曲线
逻辑斯蒂曲线是由比利时数据学家首次发现的特殊曲线，后来，生物学家皮尔(R．Pearl)和L·J·Reed根据这一理论研究人口增长规则，因此，逻辑斯蒂生长曲线也被称为生长曲线或者珍珠德曲线。逻辑斯蒂生长曲线一般形式如下：

          Yt=L1+ae-bt

L,a,b均为未知参数，需要根据历史数据进行估计。生长曲线在现代商业、生产行业、生物科学等方面有着非常广泛的应用。

我们利用生长曲线模型，拟合上海2022年3月1日到4月30日累计确诊病例数据，建立生长曲线模型。数据拟合如下图所示，蓝色部分显示的确诊病例观测值，橙色部分显示的是确诊病例预测值，并计算出3天的确诊预测病例数据（5月7日，5月8日，5月9日）。

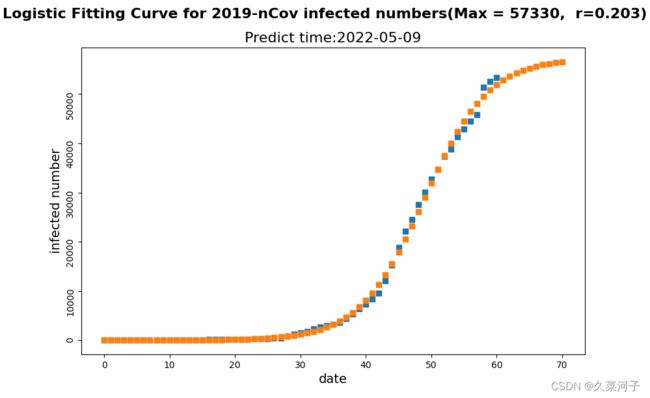
  截止本论文完成时间（5月9号），新冠确诊的实际人数是55599、55921、56155（分别为5月7日、5月8日、5月9日的数据），而根据此模型预测这三天的确诊人数分别为55926、56179、56387，可见预测值与实际值基本一致。

逻辑斯蒂拟合的代码

# -*- codeing = utf-8 -*- 
# @Time :2022/5/8 21:50 
# @File : logistics.py 
# @Software: PyCharm
import pandas as pd

csv_file = "covid19_3.csv"
df = pd.read_csv(csv_file, encoding="utf-8")
from scipy.optimize import curve_fit
import urllib
import json
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import time

csv_file = "covid19_3.csv"


def logistic_function(t, K, P0, r):
    t0 = 0
    exp = np.exp(r * (t - t0))
    return (K * exp * P0) / (K + (exp - 1) * P0)


def predict(province_code):
    predict_days = 10  # 预测未来天数

    df = pd.read_csv(csv_file, encoding="utf-8")
    df = df[df.province_code == province_code]
    confirm = df['confirmed'].values
    x = np.arange(len(confirm))

    # 用最小二乘法估计拟合
    popt, pcov = curve_fit(logistic_function, x, confirm)
    print(popt)

    # 近期情况预测
    predict_x = list(x) + [x[-1] + i for i in range(1, 1 + predict_days)]
    predict_x = np.array(predict_x)
    predict_y = logistic_function(predict_x, popt[0], popt[1], popt[2])
    ######################################################################################数据点写进mysql，目的是为了制作透明图片
    print(predict_y)

    ##########################################################################################################################
    # 绘图
    plt.figure(figsize=(15, 8))
    plt.plot(x, confirm, 's', label="confimed infected number")
    plt.plot(predict_x, predict_y, 's', label="predicted infected number")
    #     plt.xticks(predict_x, date_labels[:len(predict_x) + 1], rotation=90)
    plt.yticks(rotation=90)

    plt.suptitle(
        "Logistic Fitting Curve for 2019-nCov infected numbers(Max = {},  r={:.3})".format(int(popt[0]), popt[2]),
        fontsize=16, fontweight="bold")
    plt.title("Predict time:{}".format(time.strftime("%Y-%m-%d", time.localtime())), fontsize=16)
    plt.xlabel('date', fontsize=14)
    plt.ylabel('infected number', fontsize=14)
    plt.plot()


    plt.show()


province_codes = [1]
for province_code in province_codes:
    predict(province_code)

数据格式如下

从上图预测值生成的曲线来看，生长曲线模型整体呈现“S”型，按照相关参考文献说明，生长曲线可以分为初期、中期和末期三个阶段：

  在初期，虽然 t处于增长阶段，但是 y 的增长较为缓慢，这时曲线呈现较为平缓的上升；在中期，随着t的增长，y 的增长速度逐渐增快，曲线呈现快速上升的态势；当达到拐点(t，Y)后，因函数饱和程度的增长达到末期，随着t的增长 y 的增长较为缓慢，增长速度趋近于0，曲线呈水平状发展。

  在了解模型特点后，假设外部因素干预事件发展，就会导致数据的突然增多或减少，会影响模型的预测精度。因此，logistic增长模型只是对疾病进行预估，并不能准确判断，也并不是最佳模型。当然可以通过模型优化，来提高预测精度，有的文献提出可以根据华罗庚提出的0.618选优法，对得到的模型进行优化（计算该模型是否能得到预测值和测量值最小残差平方和）。这里我们就不再展开，可以后期进行探讨学习。

（二）疾病传播模型-SEIR
  查阅相关文献后，发现常见的传染病模型按照传染病类型分为SI、SIR、SIRS、SEIR 模型等，用于研究传染病的传播速度、空间范围、传播途径等问题，用来指导对传染病的预防和控制。模型中涉及S、E、I、R、r、β、γ、α参数：

  S类：表示易感者 (Susceptible)，指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；E类：表示暴露者 (Exposed)，指接触过感染者，但暂无能力传染给其他人的人，对潜伏期长的传染病适用；I类：表示感病者 (Infectious)，指染上传染病的人，可以传播给 S 类成员，将其变为 E 类或 I 类成员；R类：表示康复者 (Recovered)，指被隔离或因病愈而具有免疫力的人。如免疫期有限，R类成员可以重新变为 S 类。

  r：感染患者（I）每天接触的易感者数目；β：传染系数，由疾病本身的传播能力，人群的防控能力决定；γ：恢复系数，一般为病程的倒数，例如流感的病程5天的话，那么它的γ就是1/5；α：潜伏者的发病概率，一般为潜伏期的倒数。

  我们这里不再利用采集到的数据，模拟疫情发展形式，一方面原因是我们并不能较好的估计模型中涉及到各个参数, 需要考虑的的参数较多，另一方面数据并不能支撑其模型推导，特别是疫情的政府干预因素、社会舆情因素，对疫情发展趋势都会产生一定的影响，应将相关的因素考虑进去，所以这个问题相对来说是比较复杂的过程，我们这里不再进行过多探讨。大家有兴趣的可以去查找相关文献材料，进行深入研究学习。

SEIR模型代码

# -*- codeing = utf-8 -*- 
# @Time :2022/5/8 21:47 
# @Author:Liujie 
# @File : SEIR.py 
# @Software: PyCharm
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import pylab


# 计算SEIR的值
def calc(T):
    for i in range(0, len(T) - 1):
        S.append(S[i] - r * beta * S[i] * I[i] / N - r2 * beta2 * S[i] * E[i] / N)
        E.append(E[i] + r * beta * S[i] * I[i] / N + r2 * beta2 * S[i] * E[i] / N - alpha * E[i])
        I.append(I[i] + alpha * E[i] - gamma * I[i])  # 计算累计确诊人数
        R.append(R[i] + gamma * I[i])


# 画图
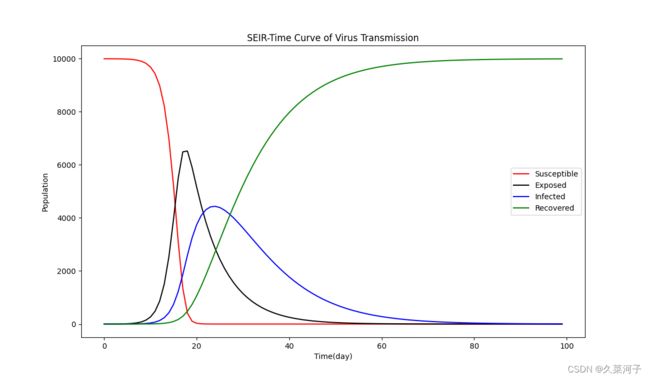
def plot(T, S, E, I, R):
    plt.figure()
    plt.title("SEIR-Time Curve of Virus Transmission")
    plt.plot(T, S, color='r', label='Susceptible')
    plt.plot(T, E, color='k', label='Exposed')
    plt.plot(T, I, color='b', label='Infected')
    plt.plot(T, R, color='g', label='Recovered')

    plt.grid(False)
    plt.legend()
    plt.xlabel("Time(day)")
    plt.ylabel("Population")
    plt.show()


S, E, I, R = [], [], [], []
N = 10000  # 人口总数
I.append(1)
S.append(N - I[0])
E.append(0)
R.append(0)
r = 20  # 传染者接触人数
r2 = 30
beta = 0.03  # 传染者传染概率
beta2 = 0.03  # 易感染者被潜伏者感染的概率
alpha = 0.14  # 潜伏者患病概率 1/7
gamma = 0.1  # 康复概率

pylab.rcParams['figure.figsize'] = (12.0, 7.0)
T = [i for i in range(0, 100)]
calc(T)
plot(T, S, E, I, R)

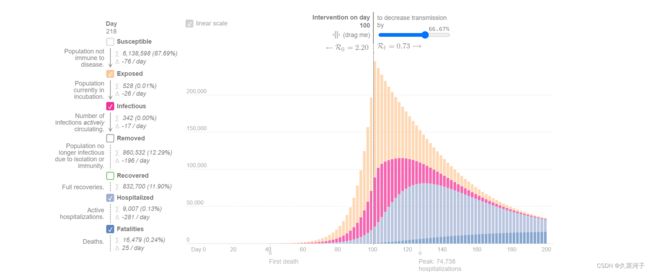
一个在线的SEIR模型可视化平台