疫情分析(4)基于流动模型的SEIR病毒模型
之前我们已经获得了疫情数据和百度迁徙的相关数据。接下来就要针对疫情进行数据建模和数据分析。
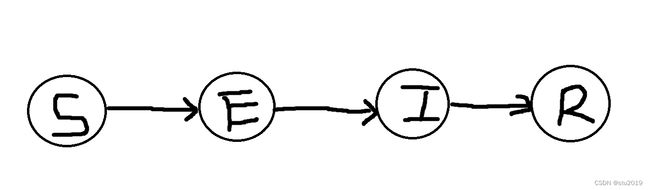
本次我们使用到的数学模型是SEIR病毒传播动力学的模型,其具体模型的内容不在本次记录中。简而言之SEIR病毒模型就是根据相关参数针对S(易感染者),E(潜伏者),I(感染者),R(康复者)的数据进行数学运算之后得到相关结果。本人针对学习了几个大佬的相关博客后
,在SEIR模型的基础上,引入新的参数和新的算法公式来对SEIR模型进行改进,做出相关的预测。
模型预测内容:假设不进行封城的举措,中国疫情形式将会是如何?也就是说封城的举措对疫情传播的发展的影响。
改进1:在SEIR模型的基础上引入D人数,和d;在传播通途上引入迁入和迁出数据作为新的易感者和潜伏期人群。
SEIR模型设计:
一:符号说明:
| 符号 | 相关意义 |
| N | 区域总人数 |
| E | 潜伏携带者 |
| I | 感染者 |
| S | 易感者 |
| R | 治愈者 |
| D | D者 |
| r | 接触人数 |
| b | 传染概率 |
| a | 潜伏者发病率 |
| y | 治愈率 |
| k | d率 |
| Move_in | 迁入人数 |
| Move_out | 迁出人 |
传统SEIR公式:
dS/dt=−rbIS/N
dE/dt = rbIS/N − aE
dI/dt=aE−yI
dR/dt=yI
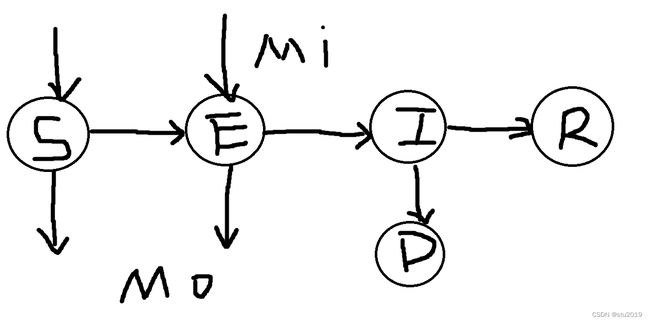
二:改进模型
改进后的SEIR模型 :
首先D和d很好引入,只需要引入列表D和d。
迁入和迁出的引入方式比较困难,我们需要首先需要假定只用S和E的人群可以自由流动,所以迁入和迁出的人群全都是S和E,在此基础上因为SEIR模型的N人口总数量的一定的(水平有限先先埋个坑,以后如果有能力再改进为N能变动的模型),所以S的人口流动是没有意义的(对原本的模型不产生影响),综上人口的流动仅仅影响E的大小。所以我们可以改进SEIR模型如下:
dS/dt=−rbIS/N
dE/dt = rbIS/N − aE+Move_in*E湖北/(N湖北)-Move_out*E/(N)
dI/dt=aE−yI-kI
dR/dt=yI
dD/dt = kI
三:相关参数的确定:
我们已经初步完成了初步改进完成的具有迁入数据影响的SEIR病毒动力模型的数学公式的推导。
下一步我们将进行参数的确定,来完成数学建模。
N:总人口:爬取各省的人口数据。
r:接触人数:通过百度百科得到没人每天平均接触20人左右
b:传播概率;和y:治愈率的求法比较特殊。
传播概率和治愈率以及d率的求法:
为什么说这三个值比较特殊,在建模起初我像直接使用国家统计出来的疫情传播概率和治愈率,但仔细思考一下这样是不正确的做法,因为首先我们模拟的是无干预下的疫情发展趋势,所以其传播率和治愈率都和现实中不一样(我们采用了封城来阻止传染源,用口罩和手套来限制传播途径,最后还用疫苗的方式来增加治愈率和d率),所以直接使用网上的统计数据是不正确的。
求法:我参考了终南山院士团队所研究的模型进行数据的分析:
假设,第一例病例和病毒自己变异形成的,所以初试感染人数就是1,S=N-1 S约等于N
所以dI/dt = rbIS/N - yI 约等于 rbI - yI = I(rb-y) 我们手动解微分方程 I = exp((rb-y)*t)
我们用早期的湖北数据拟合函数就可以算出无干预下的covid-19的传播概率和治愈率以及d率。
封城之前湖北数据17号到23号(作为拟合数据):
函数拟合:
指定的公式
x = np.arange(1, 9)
y = np.array([45, 62, 121, 198, 270, 375, 444, 549])
print(x)
print(y)
def func(x,a,b):
return np.exp((15*a-b)*x)
popt, pcov = curve_fit(func, x, y, [0.05, 0.1])#训练函数
a=popt[0]
b=popt[1]
print(a)
print(b)
yvals=func(x,a,b)
plot1=plt.plot(x, y, '*',label='original values')
plot2=plt.plot(x, yvals, 'r',label='curve_fit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4)
plt.title('curve_fit')
plt.show()人口迁徙数据的使用:
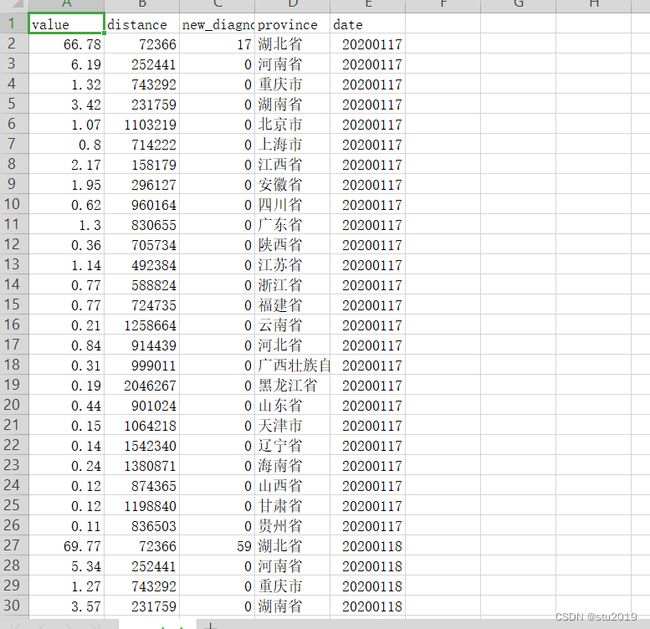
上次我们已经拿到了湖北向各省市的人口流动的数据。
计算出湖北流入其他各省的人口百分比
得到
1:2020年一月的时候,湖北向各个城市的人口流动数据百分比。
2:我们需要通过百分比计算具体值,就先得到湖北人口流动总数。
3:因为我们要计算从1月23号到之后的若干天后的疫情传播情况,1月23到2月要经历春运和之后的非春运时间,所以针对春运和非春运人口流动的情况也是大不相同的。
我们首先通过2019年春节统计数据得到春运流量大概是4000万人次。
在百度迁徙上通过计算春运时期和非春运时期的迁徙比例,大致算出非春运的人口流动情况。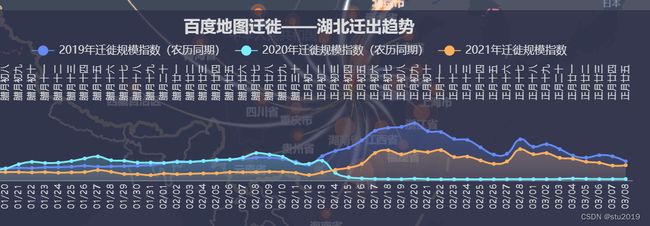
最后,我们就可以算出湖北向各个省人口流动的大致数据。
注意:在赋微分方程初值的时候,我们要将I(0) = 0 ,让第一例“感染者”是由迁入E中数据来的,这样更能真实的模拟疫情传播的情况。
四:模型的关键代码实现:
迁徙参数
N_GD = 113460000
N_HEN = 96050000
N_HUB = 59170000
N_HUN = 68990000
N_ZJ = 57370000
HU_Bei_move = 40000000
P_spring_out = int((HU_Bei_move/2 * 0.2389)/40)
P_normal_out = int((HU_Bei_move/2 * 0.2389)/80)
percent_GD = 0.008马科夫链的迭代调用。
for i in range(0, len(self.T) - 1):
self.S.append(
self.S[i] - self.r * self.b * self.S[i] * self.I[i] / self.N)
if len(self.S) <= 40:
self.E.append(self.E[i] + self.r * self.b * self.S[i] * self.I[i] / self.N - self.a * self.E[
i] + P_spring_out*percent_GD*self.E_HB[i]*100)
else:
self.E.append(self.E[i] + self.r * self.b * self.S[i] * self.I[i] / self.N - self.a * self.E[
i] + P_normal_out * percent_GD * self.E_HB[i]*100)
self.I.append(self.I[i] + self.a * self.E[i] - self.g * self.I[i] - self.I[i]*self.d)
self.R.append(self.R[i] + self.g * self.I[i])
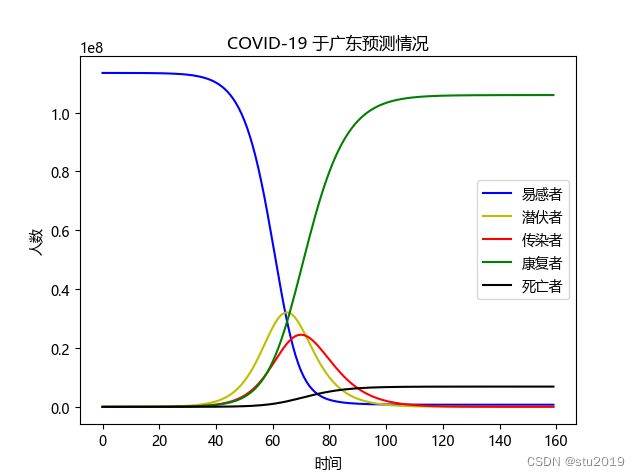
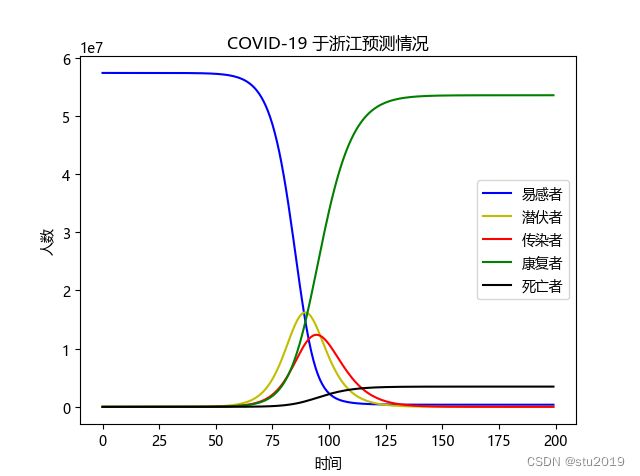
self.D.append(self.D[i] + self.I[i]*self.d)五:预测结果:
我们选取了2020年收到疫情影响最严重的两个省(广东省和浙江省)进行分析。
| 累计确诊 | 无症状感染者 | D人数 |
| 32051046 | 32051046 | 293545 |
| 累计确诊 | 无症状感染者 | 最终d人数 |
| 16206345 | 12373786 | 148485 |
通过预测结果我们可以清楚的看到封城这一举措的正确性,它有效快捷的切断了传播源头,让其他城市不受到大规模迁徙的影响。如不是封城的举措疫情将会更加肆无忌惮的弥漫开来,对我国各行各业造成不可估计的损失。
本次湖北疫情的预测到此结束,我们所构造的SEIR模型还有很多不足和没有考虑的地方,因为我想把本次重点放在刚刚发生的上海疫情上,所以本次就当练习一下。接下来我会完善和再次改进我们的SEIR模型来对上海刚刚发生的疫情进行建模和预测。届时我将会考虑疫苗等相关对疫情有很大影响的参数。