基于SIR模型的新型冠状病毒动力学建模与参数辨识（附Python代码）

0 前言

最近看了几篇关于传染病模型的科普文章觉得很有趣，于是自己动手撸了一遍。虽然貌似传染病模型和运筹学和控制论好像没有关系，实际上传染病模型很多都是动力学模型（常微分方程），这些模型我们在Control theory里边并不陌生哈。有了动力学模型也就必然会有模型参数的辨识，而模型参数的辨识往往可以被建模为一个优化问题，而优化问题的求解也是我的老本行运筹学了。

在此声明，本文的模型还是比较toy的，能有多少准确性很难保证，不过我觉得是一个很好的练手的project，毕竟作为一个科研工作者我们以我们的方式来做点什么。

1 SIR模型简介

SIR模型是常见的一种描述传染病传播的数学模型，其基本假设是将人群分为以下三类：
1 易感人群（Susceptible）：指未得病者，但缺乏免疫能力，与感病者接触后容易受到感染。
2 感染人群（Infective）：指染上传染病的人，他可以传播给易感人群。
3 移除人群（Removed）：被移出系统的人。因病愈（具有免疫力）或死亡的人。这部分人不再参与感染和被感染过程。

如下图所示，在SIR 模型中以上三类人群之间存在两个转换的关系：

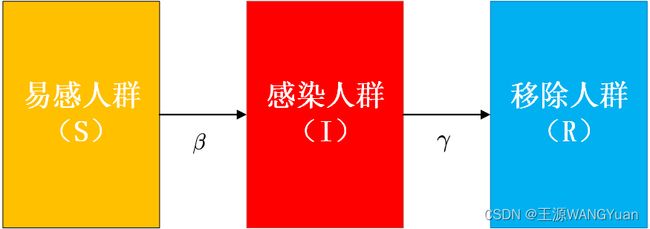
易感人群与感染人员接触时被传染，传染率为 $\beta$ 传染率反映了疾病传播的强度，传染率越大则易感人群和感染人员接触后被传染的可能性越大。

感染人群以固定平均速率 恢复或死亡。恢复率 $\gamma$，取决于感染的平均持续时间 。

简化起见分别用三类人群的首字母 $S,I,R$表示三类人群的数量，$N$ 表示人工总数。那么三类人群数量随时间的动态变化的规则可用以下常微分方程组表示：
$$\frac{dS}{dt}=-\beta \frac{SI}{N}(1)$$
$$\frac{dI}{dt}=\beta \frac{SI}{N}-\gamma I(2)$$
$$\frac{dR}{dt}=\gamma I(3)$$

2 采用优化算法对传染率进行参数辨识

通过上面的介绍我们知道SIR模型实际上是采用动力学模型（三个常微分方程）对三类人群随时间变化的过程进行建模，采用传染率和恢复率来量化描述疾病传染和疾病被治愈等行为。很重要的一点是只有获得准确的动力学模型参数才有可能建立一个相对精确的模型。那么要采用SIR模型对新型肺炎传播进行建模其主要问题就是确定出以下参数

• 1 传染率$\beta$和 恢复率$\gamma$
• 2 易感人群（Susceptible）初值，感染人群（Infective）初值，移除人群（Removed）初值

由于第一例病例是在12月8日被确诊，因此选择初始时间在12月8日。感染人群初值为1，易感人群初值为$N-1$，移除人群初值为0，其中 $N$为武汉市总人口数。$\gamma$为恢复率，因为新型冠状病毒肺炎的恢复期大约是14天，因此取 $\gamma =1/14$。因此下面我们主要是围绕如何辨识出准确的传染率 $\beta$

为了方便进行参数辨识，我们对上述SIR模型进行一个简化，我们认为在疾病传播的早期有 $S\approx N$(传播早期患病人数较少，所以可以近似认为所有人都是易感人群)，将这个条件带入到式（2）中可得
$$\frac{dI}{dt}=(\beta -\gamma )I(4)$$
易知该微分方程的通解为：
$$I(t)=C{e}^{(\beta -\gamma )t}(5)$$
由 $I(t=0)=1$可得$C=1$ ，带入式（5）中可得
$$I(t)=e^{(\beta -\gamma )t}(6)$$

由此可以构建如下参数辨识问题：

决策变量：传染率 $\beta$
目标函数： $$\min \sum _{t\in T}{\left(e^{\left(\beta -\gamma \right)t}-I\left(t\right)\right)}^2(7)$$

其中 $I$为实际的患病人数(从实际数据来)， $T$为时间集合，以天为单位。
通过求解上述优化问题即可得到新型肺炎的传染率$\beta$，易知该优化问题是一个非线性非凸的优化问题。

3 参数辨识所需数据获得与选取

从上面的参数辨识问题可以看出，我们需要武汉市的新型肺炎患病的历史数据（主要是每天的患病人数$I$）。我们从github上下载了全国主要城市1月20日至2月1日患病人数的数据(数据来源：839Studio/Novel-Coronavirus-Updates)，其数据格式如下：

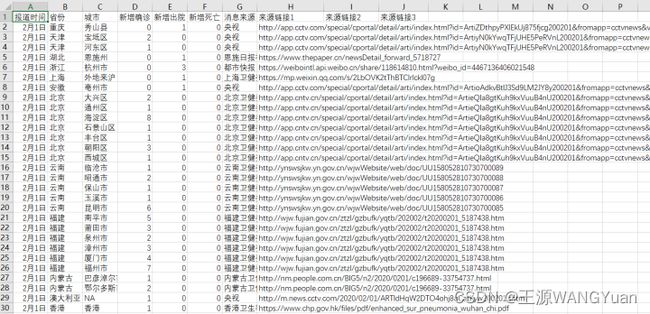
我们从中提取武汉市1月18日至1月22日的数据来进行参数辨识
为何选取18日至22日的数据？因为武汉封城是在23日，在封城之前疾病的传播受到人为因素影响较小，所以采用封城前的数据来做参数辨识。同时由于18日之前武汉患病数据统计不准确，所以18日之前的数据也不采用。
通过数据预处理后，得到用来辨识的数据格式如下所示：

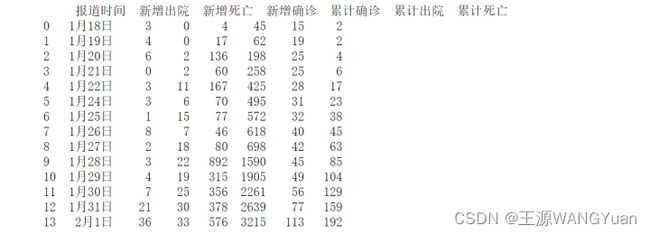
4 Python代码实现

数据处理要用到Numpy和Pandas，解微分方程和求解辨识问题需要Scipy，画图需要Matplotlib

import numpy as np
import pandas as pd
import math
import datetime
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt

主干代码分为三大块，1是数据预处理部分，主要功能是从原始数据中提取出我们辨识问题所需的数据，2是辨识问题部分，主要功能是求解优化问题，得到准确的传染率，3是SIR模型，主要是动力学模型的求解。

1 数据预处理部分，原始数据存储在Updates_NC.csv文件中，主要是提取出武汉市的数据，然后计算出每天累计患病人数，最后提取1月18日之后的数据。

Updates_NC = pd.read_csv('Updates_NC.csv')
class preProcess():
    def __init__(self):
        self.wuHan = Updates_NC[Updates_NC['城市'] == '武汉市']
        wuHanInfection = self.wuHan.groupby('报道时间')['新增确诊'].sum()
        wuHanRecovered = self.wuHan.groupby('报道时间')['新增出院'].sum()
        wuHanDead = self.wuHan.groupby('报道时间')['新增死亡'].sum()
        self.wuHan = {'报道时间':wuHanInfection.index, '新增确诊':wuHanInfection.values, '新增出院': wuHanRecovered.values, '新增死亡':wuHanDead.values}
        self.wuHan = pd.DataFrame(self.wuHan, index = [i for i in range(wuHanInfection.shape[0])])
    
    def getTotal(self):
        wuHanTotalInfection = [self.wuHan.loc[0:i,'新增确诊'].sum() for i in range(self.wuHan.shape[0])]
        wuHanTotalRecovered = [self.wuHan.loc[0:i,'新增出院'].sum() for i in range(self.wuHan.shape[0])]
        wuHanTotalDead = [self.wuHan.loc[0:i,'新增死亡'].sum() for i in range(self.wuHan.shape[0])]
        self.wuHan = self.wuHan.join(pd.DataFrame([wuHanTotalInfection,wuHanTotalRecovered ,wuHanTotalDead], index = ['累计确诊', '累计出院','累计死亡']).T)
        print(self.wuHan)
    
    def removeNoisyData(self):
        self.wuHan = self.wuHan[self.wuHan['报道时间'] >= '1月18日']
        self.wuHan.index = [i for i in range(self.wuHan.shape[0])]
        print(self.wuHan)
        
    def report(self):
        plt.plot(self.wuHan.index, self.wuHan['累计确诊'])
        plt.xlabel('Day')
        plt.ylabel('Number of people(Wu Han)')
        plt.show()

2 定义出参数辨识问题，主要是定义出目标函数（costfunction）即可调用Scipy来帮助我们求解优化问题。实际上在代码中我们在求解辨识问题的时候，将传染率拆成了2项相乘的形式 $\beta =nContact\times infectionProb$，其中$nContact$为感染人员每天接触的正常人的数量（假设为5人），$infectionProb$ 为感染概率

class estimationInfectionProb():
    def __init__(self, estUsedTimeIndexBox, nContact, gamma):
        self.timeRange = np.array([i for i in range(estUsedTimeIndexBox[0],estUsedTimeIndexBox[1] + 1)])
        self.nContact, self.gamma = nContact, gamma
        self.dataStartTimeStep = 41
    
    def setInitSolution(self, x0):
        self.x0 = 0.04
        
    def costFunction(self, infectionProb):
        #print(infectionData.wuHan.loc[self.timeRange - self.dataStartTimeStep,'累计确诊'])
        #print(np.exp((infectionProb * self.nContact - self.gamma) * self.timeRange))
        res = np.array(np.exp((infectionProb * self.nContact - self.gamma) * self.timeRange) - \
                       infectionData.wuHan.loc[self.timeRange - self.dataStartTimeStep,'累计确诊'])
        return (res**2).sum() / self.timeRange.size
    
    def optimize(self):
        self.solution = minimize(self.costFunction, self.x0, method='nelder-mead', options={'xtol': 1e-8, 'disp': True})
        print('infection probaility: ', self.solution.x)
        return self.getSolution()
    
    def getSolution(self):
        return self.solution.x
    
    def getBasicReproductionNumber(self):
        self.basicReproductionNumber = self.nContact * self.solution.x[0] / (self.gamma)
        print("basic reproduction number:", self.basicReproductionNumber)
        return self.basicReproductionNumber

定义出SIR 模型的类，代码写得比较直观和简单，此处就不多解释了，相信很容易看懂。主要是用scipy来求解常微分方程，即式（1-3）。需要注意的是此处的传染率 $\beta$ 要用上面参数辨识得到的值。

class wuHanSIRModel():
    def __init__(self, N, beta, gamma):
        self.beta, self.gamma, self.N = beta, gamma, N
        self.t = np.linspace(0, 360, 361)
        self.setInitCondition()
    
    def odeModel(self, population, t):
        diff = np.zeros(3)
        s,i,r = population
        diff[0] = - self.beta * s * i / self.N
        diff[1] = self.beta * s * i / self.N - self.gamma * i
        diff[2] = self.gamma * i
        return diff
    
    def setInitCondition(self):
        self.populationInit = [self.N - 1, 1, 0]
        
    def solve(self):
        self.solution = odeint(self.odeModel,self.populationInit,self.t)
    
    def report(self):
        #plt.plot(self.solution[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
        plt.plot(self.solution[:,1],color = 'orange',label = 'Infection',marker = '.')
        plt.plot(self.solution[:,2],color = 'green',label = 'Recovery',marker = '.')
        plt.title('SIR Model' + ' infectionProb = '+ str(infectionProb))
        plt.legend()
        plt.xlabel('Day')
        plt.ylabel('Number of people')
        plt.show()

最近在家上github很慢，我就把全套代码放到网盘上吧。网盘链接如下： https://pan.baidu.com/s/1X4oiPhU5d8CQX01DOg6zPA 提取码: abqa

5 结果分析

5.1 武汉市患病人数分析

如下图所示是武汉市患病人数数据，用红色框圈出的是累计患病人数，可以很明显地看到从1月11日至1月18日的累计患病人数基本保持不变。

5.2 传染率辨识结果分析

我们得到的辨识结果为 infection probaility: 0.03926041，传染率 $\beta =0.19630$
同时可以采用如下公式估算出 新型肺炎病毒基本传染数（basic reproduction number）
$$R_0=\frac{\beta }{\gamma }=0.19630/(1/14)=2.74822898865$$

$R_0$ 基本传染数是指在没有外力介入，同时所有人都没有免疫力的情况下，一个感染某种传染病的人，会把疾病传染给其他多少个人的平均数，基本传染数是衡量疾病传染性的一个重要指标。若$R_0<1$则传染病将会逐渐消失，若$R_0>1$传染病会以指数方式散布，成为流行病。非典的基本传染数约为0.85-3，埃博拉基本传染数约1.5-2.5。

5.3 用SIR模型预测武汉市患病人数

定义nContact为 每个患病人员每天会接触nContact个正常人，nContact越大表明隔离和管制措施越弱，同时接触后正常人的患病概率为0.03926的情况下SIR模型结果如下
即若不采取任何管制和防控措施的条件下，假设nContact=5，武汉市患病人数随时间变化的曲线如下所示：

当nContact=4，武汉市患病人数随时间变化的曲线如下所示：

当nContact=3，武汉市患病人数随时间变化的曲线如下所示：

当nContact=2 (表明已经采用了比较严厉的隔离和管制措施)，武汉市患病人数随时间变化的曲线如下所示：

从上面的结果可以非常清晰得看出随着nContact的减少，患病人数急剧减少，当nContact=2时 患病人数甚至不超过100人，可见采取严厉的管制和防控隔离措施对新型冠状病毒患病人数的减少有着非常明显的效果。

6 总结

• 采用动力学模型对疾病传播建模并不难，难点在于如何利用真实数据辨识动力学模型中的参数。
• 对真实数据的收集，预处理等工作看起来不起眼，实际上在我们的工作中是一个非常重要的部分。
• SIR模型还是比较粗糙的一个模型，主要是没有考虑到潜伏期，那么SEIR模型会更加精确一些，后期有兴趣可以再做一做。
• 还可以考虑两阶段的模型，例如武汉市在1月23日采取了封城措施，那么可以将封城前后分别进行建模，构成一个两阶段模型会更加准确一些。

参考文献

【1】新型冠状病毒的疫情评估与预测报告，北京航空航天大学计算机学院智慧城市（BIGSCity）课题组和经管学院数据智能（DIG）课题组
【2】https://zhuanlan.zhihu.com/p/103974270
【3】https://zhuanlan.zhihu.com/p/104371621