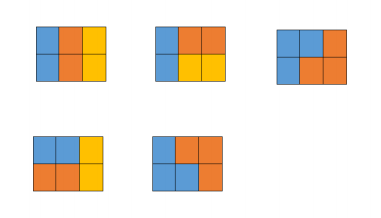蓝桥杯2022年第十三届省赛真题-积木画
写在前面
这道题我有在网上去搜索了一下其他博主的题解,因为我实在无法理解 d p [ i ] = d p [ i − 1 ] ⋅ 2 + d p [ i − 3 ] dp[i] = dp[i-1]\cdot2+dp[i-3] dp[i]=dp[i−1]⋅2+dp[i−3] 这个状态转移方程是如何得到的(可能是自己太笨了),他们的题解大多都是草草两句收尾讲的有些含糊不清,作为菜狗的我真的很难懂啊啊啊啊!在思考良久后对于这道题我想到了一种自己的解题想法,与网上主流的状态转移方程不同不过同样能够解题。
蓝桥杯2022年第十三届省赛真题-积木画
时间限制: 1Sec 内存限制: 256MB 提交: 623 解决: 135
题目描述
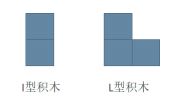
小明最近迷上了积木画,有这么两种类型的积木,分别为 I 型(大小为 2 个单位面积)和 L 型(大小为 3 个单位面积):
同时,小明有一块面积大小为 2 × N 的画布,画布由 2 × N 个 1 × 1 区域构成。小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式? 积木可以任意旋转,且画布的方向固定。
输入
输入一个整数 N,表示画布大小。
输出
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 取模后的值。
样例输入复制
3
样例输出复制
5
提示
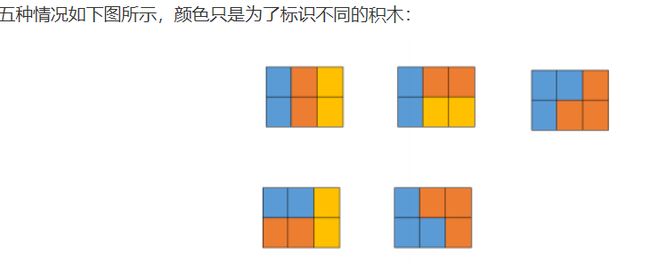
五种情况如下图所示,颜色只是为了标识不同的积木:
对于所有测试用例,1 ≤ N ≤ 10000000.
解题思路1️⃣:
哎,但凡是比赛的时候再测一个数据也不会不过,太可惜了,但是写的时候思路是对的,可惜a[2][1]写错了。
思路:a[i][0]:i列积木的堆法,a[i][1]:i列多一块小方格的堆法。
如:

或者

不管这三块是怎么放的,都叫a[3][0].
如果在此基础上右边多一个小方格就叫a[3][1],注意小方格可以在第四列上一行也可以在第四列下一行(不好找图就不给了,自行想象)
给出动态规划方程:
a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;
a[i][1]=(a[i-1][0]*2+a[i-1][1])%mod;
画布大小为i的排法,既a[i][0]的值:
- 先考虑少一块I型积木的排法,既a[i-1][0],这时加上一块I型积木就行了,
- 再考虑少一块L型积木的排法,既a[i-2][1],这时加上一块L型积木就行了,
- 考虑少两块I型积木的排法,既a[i-2][0],加上两块I型积木,注意,两块必需横着加进去,如果是竖着加,就相当于第一种类型排法了,重复了。
- 涉及缺更多积木时,会发现无论怎么排,排法都会和上述情况重复,也就是说,以上三种情况涵盖了a[i][0]的所有排法。
所以有:
a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;
a[i][1]的排法,大家可以自行画图写出来。
写出初始状态:
a[1][0]=1,a[2][0]=2,a[1][1]=2,a[2][1]=4;
给出完整代码:
#include解体思路2️⃣:
首先这个题肯定是用动态规划来做的,正好它也符合动态规划做题的思想,无后效性也满足所以我们用动态规划做会好做一点.
那怎么想这个题呢,首先它是二维的一个矩阵模式,并且有摆放还是有顺序的,所以我们如果要用二维dp来做还确实不好做,拿我们所幸直接用一维来简化拼积木的过程,但是怎么简化呢.
我们先来看下题目给的案例:
首先我们直接来看三阶的,第一个和第二个我们可以发现I型积木拼放的方式是有2种的,或者看一和四都行,然后L型积木的拼接方式是1种看三和五(你把他们两个反转过来就是一种),那我们不妨想的简单一点所以递推公式就是:dp[i]=dp[i-1]*2+dp[i-3];
证明的方法就是我们刚才的思想过程,我们讲二维的矩阵看成了一维的,所以I型积木就是等于1个方格,所以我们记为i-1,L型积木就是等于1.5个方格,但是L型积木不能单独出现,必须成双的出现,所以我们记为i-3,又由于I型积木出现在一个位置有两种方式,所以我们乘以二,L型积木出现只有一直方式我们乘以1,就结束了。
但是我们还要进行初始化前三个:
当i等于1的时候dp就是1,这个没啥说的,只能放一种I型不管咋放都一样.
当i等于2的时候dp是2,因为可以放两个I型,可以水平放可以竖直放2种.
当i等于3的时候就是题目当中的情况dp等于5,
参考代码:
#include解题思路3️⃣:
状态表示
本题解题的关键是使用动态规划,定义一维数组 d p dp dp , d p [ i ] dp[i] dp[i] 存储画布的大小为 2 × i 2\times i 2×i 时积木的填充方法数。
状态初始化
不难发现:
- 当画布大小为 2 × 1 2\times 1 2×1 时,只能放下一个 I 型积木,因此 d p [ 1 ] = 1 dp[1] =1 dp[1]=1。
当画布大小为 2 × 2 2\times 2 2×2 时,只能放下两个 I 型积木,但积木可以旋转,如下图所示,因此 d p [ 2 ] = 2 dp[2] = 2 dp[2]=2
当画布大小为 2 × 3 2\times3 2×3时,如题目中所示,共有五种方式,因此 d p [ 3 ] = 5 dp[3] = 5 dp[3]=5
情况梳理
梳理状态转移方程之前,不妨思考下,积木画出现在最后且符合题意的积木块只能出现哪几种情况呢?
情况一:单独使用 I 型积木拼接
完全可以使用单独的
拼接在任意一个符合题意的积木画尾部中,使积木画总长度 + 1。
情况二:使用两个 I 型积木拼接
使用
同样能够拼接到任意一个符合题意的积木画尾部,使其积木画总长度 + 2。
情况三:使用两个 L 型积木拼接
使用
或
拼接到任意一个符合题意的积木画尾部,使其积木画总长度 +3,但要注意此时存在这两种 L 型积木拼接方式属于不同的方式,因此需要单独计算!
情况四:使用两个 L 型积木与 i ( 1 , 2 , 3 , . . . . n ) i(1,2,3,…n) i(1,2,3,…n) 个 I 型积木拼接
最容易被忽略的情况!使用 I 型积木与 两个 L 型积木同样能完成拼接。
不要忘记翻转后的情况:
状态转移方程
-
情况一:单独使用 I 型积木拼接, d p [ i ] + = d p [ i − 1 ] dp[i] += dp[i-1] dp[i]+=dp[i−1]
-
情况二:使用两个 I 型积木拼接, d p [ i ] + = d p [ i − 2 ] dp[i]+=dp[i-2] dp[i]+=dp[i−2]
-
情况三:使用两个 L 型积木拼接, d p [ i ] + = 2 ⋅ d p [ i − 3 ] dp[i]+=2\cdot dp[i-3] dp[i]+=2⋅dp[i−3]
-
情况四:情况四只有 i > = 4 i>=4 i>=4 时才可能出现,具体讨论如下:
-
若 i = = 4 i4 i4 ,只存在长度为 4 的拼接情况,假设 d p [ 0 ] = 1 dp[0]=1 dp[0]=1,也就是说 d p [ 4 ] + = d p [ 0 ] ⋅ 2 dp[4]+=dp[0]\cdot 2 dp[4]+=dp[0]⋅2
-
若 i = = 5 i5 i5,存在长度为 4 , 5 4,5 4,5 的拼接情况,即 d p [ 5 ] + = ( d p [ 0 ] + d p [ 1 ] ) ⋅ 2 dp[5] += (dp[0]+dp[1])\cdot 2 dp[5]+=(dp[0]+dp[1])⋅2
-
若 i = = 6 i 6 i6,继续推导有: d p [ 6 ] + = ( d p [ 0 ] + d p [ 1 ] + d p [ 2 ] ) ⋅ 2 dp[6]+=(dp[0]+dp[1]+dp[2])\cdot 2 dp[6]+=(dp[0]+dp[1]+dp[2])⋅2
-
若 i = = 7 i7 i7,推导有: d p [ 7 ] + = ( d p [ 0 ] + d p [ 1 ] + d p [ 2 ] + d p [ 3 ] ) ⋅ 2 dp[7]+=(dp[0]+dp[1]+dp[2]+dp[3])\cdot 2 dp[7]+=(dp[0]+dp[1]+dp[2]+dp[3])⋅2
按照上述推导,不难发现 d p [ i ] + = ( d p [ 0 , 1 , 2 , . . . , i − 4 ] ) ⋅ 2 dp[i]+=(dp[0,1,2,…,i-4])\cdot 2 dp[i]+=(dp[0,1,2,…,i−4])⋅2,因此可以定义一个变量 s u m sum sum 存储 d p [ 0 , 1 , 2 , . . i ] dp[0,1,2,…i] dp[0,1,2,…i] 的值,在 i i i 增大的同时更新 s u m sum sum 的值,初始情况 s u m = 0 sum=0 sum=0。
返回结果
最终 d p [ N ] dp[N] dp[N] 就是题目所求值,这道题就这样解决了。
需要注意:下面代码中仅使用 a 1 , a 2 , a 3 a1,a2,a3 a1,a2,a3 分别代表 d p [ i − 1 ] , d p [ i − 2 ] , d p [ i − 3 ] dp[i-1],dp[i-2],dp[i-3] dp[i−1],dp[i−2],dp[i−3]。
代码编写
#include 写在最后
如果有哪里看不懂,可以评论区或者私信我,
如果觉得对你有用,就给本蒟蒻一个好评吧。