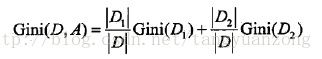实验四 决策树

代码地址 Github

题目：

某连锁餐饮企业想了解周末和非周末对销量是否有很大影响，以及天气好坏、是否有促销活动对销量的影响，从而公司的辅助决策。现有单个门店的历史数据。请按要求完成实验。建议使用python 编程实现。

数据集：

文件ex3data.xls 为该实验的数据集，第1-5 列分别表示序号、天气好坏、是否周末、是否有促销和销量高低。

实验要求：

选择ID3、C4.5、CART 三种常见决策树算法中的一种建立决策树模型，并画出决策树。（采用多种算法实现并进行算法的比较分析者，将获得更高分数）

文件的读取:

本次文件不是之前的txt文件，而是excel文件。所以需要重写readfile函数。

def read_xls_file():                            #读取excel文件
    data = xlrd.open_workbook('./ex3data.xls')  #打开文件
    sheet1 = data.sheet_by_index(0)             #获取sheet
    m = sheet1.nrows                            #获取行大小
    n = sheet1.ncols                            #获取列大小
    dataMat = []                         
    label = []                                  #标签
    for i in range(m):                          #枚举每一行
        row_data = sheet1.row_values(i)         #获取一行数据
        del(row_data[0])                        #删除第一列元素
        if(i == 0):                             #标签
           label = row_data                     #获取标签 
        elif(i > 0 ):                           #其他数据      
           dataMat.append(row_data)
    return dataMat,label

得到特征：

得到数据：

决策树模型

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部节点和叶节点，内部节点表示一个特征或属性，叶节点表示一个类。分类的时候，从根节点开始，当前节点设为根节点，当前节点必定是一种特征，根据实例的该特征的取值，向下移动，直到到达叶节点，将实例分到叶节点对应的类中。

决策树学习

决策树学习算法包含特征选择、决策树的生成与剪枝过程。决策树的学习算法一般是递归地选择最优特征，并用最优特征对数据集进行分割。开始时，构建根节点，选择最优特征，该特征有几种值就分割为几个子集，每个子集分别递归调用此方法，返回节点，返回的节点就是上一层的子节点。直到数据集为空，或者数据集只有一维特征为止。

信息熵

对于一个可能有n种取值的随机变量：

其熵为：

X的熵与X的值无关，只与分布有关，所以也可以将X的熵记作H(p)，即:

条件熵H(Y|X)

表示在已知随机变量X的条件下随机变量Y的不确定性，定义为在X给定的条件下，Y的条件概率分布对X的数学期望：

信息增益

信息增益表示得知特征X的信息而使类Y的信息的熵减少的程度。形式化的定义如下：

特征的选取

如何判断一个特征的分类能力呢？信息增益大的特征具有更强的分类能力。只要计算出各个特征的信息增益，找出最大的那一个就行。形式化的描述如下：

分类函数

def classify(inputTree,featLabels,testVec):  #根据已有的决策树，对给出的数据进行分类
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)  #这里是将标签字符串转换成索引数字
    for key in secondDict.keys():
        if testVec[featIndex] == key:       #如果key值等于给定的标签时
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key],featLabels,testVec) #递归调用分类
                #print classLabel
            else: classLabel = secondDict[key] #此数据的分类结果

    return classLabel

ID3算法

从根节点开始，计算所有可能的特征的信息增益，选择信息增益最大的特征作为当前节点的特征，由特征的不同取值建立空白子节点，对空白子节点递归调用此方法，直到所有特征的信息增益小于阀值或者没有特征可选为止。

算法实现：

def id3(data):
    numFeatures = len(data[0]) - 1  # 最后一列是分类
    base = shannon_data(data)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):  # 遍历所有维度特征
        infoGain = Infor_Gain(data, base, i)
        if (infoGain > bestInfoGain):  # 选择最大的信息增益
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature  # 返回最佳特征对应的维度

调用ID3算法生成决策树

def createTree(data, labels):
    classlist = [example[-1] for example in data]
    if classlist.count(classlist[0]) == len(classlist):
       return classlist[0]
    if len(data[0]) == 1:
       return majority(classlist)
    bestfeat = id3(data)
    bestfeatlabel = labels[bestfeat]
    mytree = {bestfeatlabel:{}}
    del(labels[bestfeat])
    featvalues = [example[bestfeat] for example in data]
    unique = set(featvalues)
    for value in unique:
        sublabel = labels[:]
        mytree[bestfeatlabel][value] = createTree(splitData(data,bestfeat, value),sublabel)
    return mytree

正确率

算法运行时间

决策树

C4.5算法

C4.5算法与ID3相似，但是在选择的时候使用的是信息增益比，形式化地描述如下：

代码实现：

def C4_5(data):
    numFeatures = len(data[0]) - 1  # 最后一列是分类
    baseEntropy = shannon_data(data)
    bestInfoGainRate = 0.0
    bestFeature = -1
    for i in range(numFeatures):  # 遍历所有维度特征
        infoGainRate = Infor_GainRate(data, baseEntropy, i)
        if (infoGainRate > bestInfoGainRate):  # 选择最大的信息增益
            bestInfoGainRate = infoGainRate
            bestFeature = i
    return bestFeature  # 返回最佳特征对应的维度

调用c4.5算法生成决策树

def createTree(data, labels):
    classlist = [example[-1] for example in data]
    if classlist.count(classlist[0]) == len(classlist):
       return classlist[0]
    if len(data[0]) == 1:
       return majority(classlist)
    bestfeat = C4_5(data)
    bestfeatlabel = labels[bestfeat]
    mytree = {bestfeatlabel:{}}
    del(labels[bestfeat])
    featvalues = [example[bestfeat] for example in data]
    unique = set(featvalues)
    for value in unique:
        sublabel = labels[:]
        mytree[bestfeatlabel][value] = createTree(splitData(data,bestfeat, value),sublabel)
    return mytree

正确率

算法运行时间

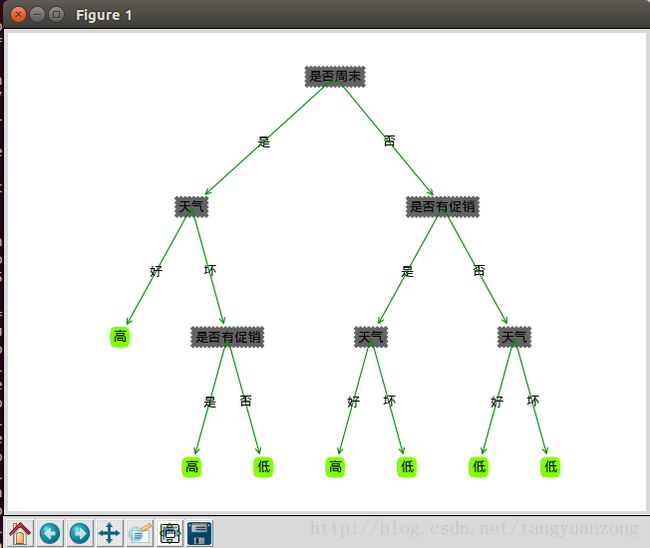
决策树

居然是一样的结果。。

CART算法

CART生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选取，生成二叉树。与回归树算法流程类似，只不过选择的是最优切分特征和最优切分点，并采用基尼指数衡量。基尼指数定义：

对于给定数据集D，其基尼指数是：

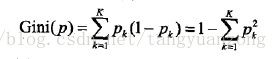
Ck是属于第k类的样本子集，K是类的个数。Gini(D)反应的是D的不确定性（与熵类似），分区的目标就是降低不确定性。

D根据特征A是否取某一个可能值a而分为D1和D2两部分：

则在特征A的条件下，D的基尼指数是：

python实现：

def cart(dataSet):
    numFeatures = len(dataSet[0]) - 1
    bestGini = 999999.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        gini = 0.0
        for value in uniqueVals:
            subDataSet = splitData(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            subProb = len(splitData(subDataSet, -1, 'N')) / float(len(subDataSet))
            gini += prob * (1.0 - pow(subProb, 2) - pow(1 - subProb, 2))
        if (gini < bestGini):
            bestGini = gini
            bestFeature = i
    return bestFeature

正确率

算法运行时间

决策树

正确率没变，但是得到的决策树不一样。

算法比较

在本次实验中，三种算法的正确率是一样的

ID3和C4.5生成的决策树是一样的。但是C4.5算法的运行时间更少。
CART生成的决策树不一样，运行时间最少。

决策树的存储

我们可以将决策树存入文档。

def storeTree(inputTree, filename): #储存决策树
    import pickle
    fw = open(filename, 'wb')
    pickle.dump(inputTree, fw)
    fw.close()

def grabTree(filename): #读取决策树
    import pickle
    fr = open(filename, 'rb')
    return pickle.load(fr)

存储并调用决策树

storeTree(myTree,"./tree.txt")
tree = grabTree("./tree.txt")
createPlot(tree)

打印决策树（使用CART生成的决策树）

我们发现是一样的。

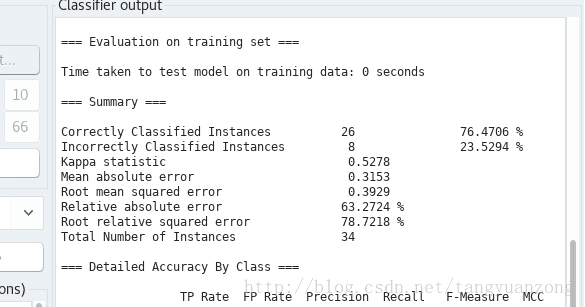
与Weka的比较

神经网络进行分类：

正确率和运行时间

可视化

Random Tree

正确率和运行时间

决策树

我们发现，通过WeKa求解的正确率和我们求解的结果是一样的。决策树有点不一样。程序的运行时间无太大差异。