二叉树链式结构
typora-copy-images-to: upload
文章目录
- 前言
- 二叉树的链式结构
- 二叉树的遍历方式
-
- 前序遍历
- 中序遍历
- 后序遍历
- 二叉树前中后序遍历练习
-
- 前序遍历练习
- 中序遍历练习
- 后序遍历练习
- 利用前序遍历中序遍历结合
- 二叉树其他操作
-
- 二叉树结点个数
- 二叉树叶子结点个数
- 二叉树第K层节点个数
- 二叉树查找值为x的节点
- 二叉树的高度
- 二叉树的层序遍历
前言
上一章讲到二叉树的顺序结构实现以及运用,而此篇文章是为了讲解二叉树的链式结构以及相关运用.
二叉树的链式结构
如果想用链式结构进行实现二叉树,那么一定少不了左右指针(指向孩子),所以实现结构如下:
typedef char BTDataType;
typedef struct BinaryTree
{
BTDataType val;
struct BinaryTree* left;
struct BinaryTree* right;
}BTNOde;
二叉树的遍历方式
二叉树的遍历方式主要有四种,前面先介绍3种,最后再介绍第四种.
- 第一种,前序遍历,方式为先遍历根结点,左子树,右子树
- 第二种,中序遍历,方式为先遍历左子树,根结点,右子树
- 第三种,后序遍历,方式为先遍历左子树,右子树,根结点
其中这三种遍历方式一般都用递归进行实现.
前序遍历
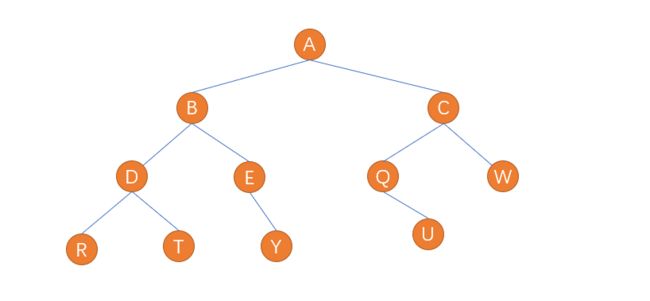
上面已经说到,前序遍历方式为根结点—>左子树—>右子树,我们用下图为例
按照前序遍历方式,其遍历顺序为A–>B–>D–>R–>T–>E–>Y–>C–>Q–>U–>W,这个答案可能和大家想的不一样,理由就是没有明白我们的遍历方式.按照前序遍历方式,我们应该先遍历根结点,即A,然后遍历左子树,当进入左子树后,我们是需要又执行前序遍历方式,即遍历根结点B,然后又要遍历左子树,当我们再进入左子树,又是先遍历根结点即D,然后又遍历左子树,按照顺序遍历到R,此时终于完成 根结点,左子树,我们遍历右子树,进入右子树后又遍历根结点,即T…所以我们的这种遍历方式其实递归性质的.
前序遍历代码:
void PreOreder(BTNode* root)
{
if(!root) return ; //如果为空结点,直接打印NULL
printf("%c-->",root->val); //遍历根结点
PreOreder(root->left); //遍历左子树
PreOreder(root->right); //遍历右子树
}
测试:
中序遍历
中序遍历方式为左子树,根结点,右子树,所以仍以上面的图为例,我们的遍历方式顺序为:
R–>D–>T–>B–>E–>Y–>A–>Q–>U–>C–>W
中序遍历代码:
void InOrder(BTNode* root)
{
if(!root) return; //如果当前结点为空,直接结束
InOrder(root->left); //遍历左子树
printf("%c",root->val); //打印当前结点值
InOrder(root->right); //遍历右子树
}
测试:
后序遍历
后序遍历方式为 左子树,右子树,根结点.,按照上面的图示,我们得出的遍历顺序应该如下:
R–>T–>D–>Y–>E–>B–>U–>Q–>W–>C–>A
后序遍历代码如下:
void PostOrder(BTNode* root)
{
if(!root) return; //如果当前结点为空,直接结束
InOrder(root->left); //遍历左子树
InOrder(root->right); //遍历右子树
printf("%c",root->val); //打印当前结点值
}
测试:
二叉树前中后序遍历练习
前序遍历练习
中序遍历练习
后序遍历练习
利用前序遍历中序遍历结合
二叉树其他操作
二叉树结点个数
按照递归思想,计算二叉树的结点数量,我们可以认为
数量 = 1 + 左子树数量 + 右子树数量,其中1是当前根结点数量(前提是存在)
int BinaryTreeSize(BTNode* root)
{
if(!root) return 0;
int left = BinaryTreeSize(root->left);
int right = BinaryTreeSize(root->right);
return 1 + left + right;
}
二叉树叶子结点个数
按照递归思想,计算二叉树的叶子结点数量,我们可以认为
数量等于 = 0 + 左子树叶子结点数量 + 右子树叶子结点数量,0是因为当前根结点有子树,说明根结点不是叶子结点.
int BinaryTreeLeafSize(BTNode* root)
{
if(!root) return 0;
if(root->left == NULL && root->right == NULL) return 1;
int left = BinaryTreeLeafSize(root->left);
int right = BinaryTreeLeafSize(root->right);
return left + right;
}
二叉树第K层节点个数
第k层是指从根结点开始算第一层,往下到第K层.
按照递归思想我们反过来,根结点是第k层,后面向下k逐渐递减,k等于1时候便是我们所求.
而数量等于左子树第k层加上右子树第k层.
int BinaryTreeKSize(BTNode* root,int k)
{
if(!root) return 0;
if(k==1) return 1;
int left = BinaryTreeLeafSize(root->left,k-1);
int right = BinaryTreeLeafSize(root->right,k-1);
return left + right;
}
二叉树查找值为x的节点
按照递归思想,先判断当前结点是否是目标,然后查找左子树,再查找右子树.
如果左右子树都没有找到,就返回
NULL
BTNode* BinaryTreeFind(BTNode* root, int n)
{
if(!root) return NULL;
if(root->val == n) return root;
BTNode* left = BinaryTreeFind(root->left,n);
if(left) return left;
BTNode* right = BinaryTreeFind(root->right,n);
if(right) return right;
return NULL;
}
二叉树的高度
按照递归思想,二叉树的高度等于1 + 左右子树高度的最大值.
int BinaryTreeDepth(BTNode* root)
{
if(!root) return 0;
int left = BinaryTreeDepth(root->left);
int right = BinaryTreeDepth(root->right);
int maxval = left < right ? right : left;
return 1 +maxvalue;
}
二叉树的层序遍历
层序遍历我们一般需要使用队列,什么是程序遍历呢?
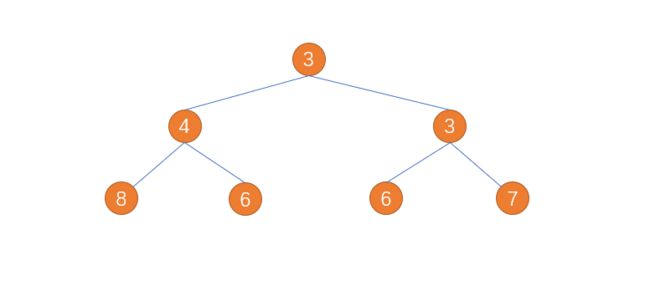
层序遍历就是遍历顺序是**整整一层,**以下图为例:
程序遍历结果为: 3-->4-->3-->8-->6-->6-->7.
而我们利用队列是怎样进行实现呢?答案是先进去一个结点,再出去一个结点,但是结点出去之前,孩子按左右顺序进入.
如下图:
我们前面已经实现过了队列的各种操作,这里便不再续写队列,直接引用.
队列定义细节修改:
typedef struct BinaryTree QDataType;
typedef struct Queue
{
QdataType* val;
struct Queue* next;
}Queue;
层序遍历:
int main()
{
Queue q = {0};
BTNode* tree = CreateTree();
QueueInit(&q);
QueuePush(&q,tree);
while(!QueueEmpty(&q))
{
BTNode* top = QueueFront(&q);
QueuePop(&q);
if(top->left) QueuePush(&q,top->left);
if(top->right) QueuePush(&q,top->right);
printf("%c ",top->val);
}
return 0;
}