C++刷题笔记(40)——股票问题、leetcode121、122、123、188、309、714
股票问题
写在前面
解决股票问题的一种常用方法就是将 买入 和 卖出 分开考虑
买入为负收益、卖出为正收益,尽可能地降低负收益、提高正收益就可以得到最大利润。
题目1:121.买卖股票的最佳时机Ⅰ(只能买卖一次)
一维数组
1.确定dp数组以及下标的含义
dp[i]:从[0,i]天能获得的最大利润dp[i]
2.确定状态转移方程
想获得最大利润,只能买卖一次,那么肯定要从低点买入、高点卖出
假设在第 i 天,
如果第i天卖出可以获得最大利润,那么就是第i天的价格减去最低价格,即prices[i]-minprice
如果第i天卖出比i-1天获得的利润小,那么最大利润就是dp[i-1]
那么状态转移方程为:dp[i] = max(dp[i-1], prices[i]-minprice);
3.dp数组初始化
dp[0] = 0,第一天不会有利润
4.确定遍历顺序
通过递推公式可得是从前往后遍历
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
int minprice = prices[0];
vector<int> dp(prices.size(), 0);
for (int i = 1; i < prices.size(); i++) {
minprice = min(prices[i], minprice);
dp[i] = max(dp[i - 1], prices[i] - minprice);
}
return dp[prices.size() - 1];
}
};
二维数组
1.确定dp数组以及下标的含义
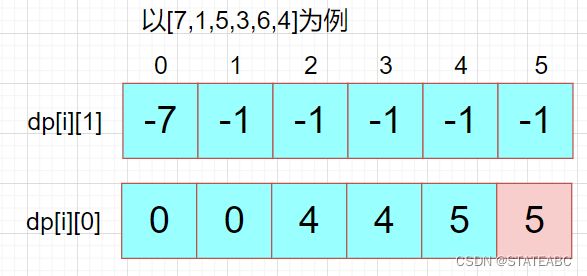
dp[i][0]表示第 i 天交易完后手里没有股票的最大利润
dp[i][1]表示第 i 天交易完后手里持有一只股票的最大利润
2.确定状态转移方程
dp[i][0]的状态转移方程:
第i天不持有股票,那么有两种可能:①第i-1天就已经不持有股票了,即dp[i-1][0];②第i-1天时持有股票(即dp[i-1][1]),在第i天卖掉,即dp[i-1][1]+prices[i]。
那么dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1]的状态转移方程:
第i天持有股票,那么也有两种可能:①第i-1天已经持有了一支股票,即dp[i-1][1];②第i-1天不持有股票(即dp[i-1][0]),那么需要在第i天买入,即-prices[i]。
那么dp[i][1] = max(dp[i-1][1], - prices[i])
3.dp数组初始化
dp[0][1] = -prices[0],表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来
dp[0][0] = 0,表示第0天不持有股票,不持有股票那么现金就是0
本题中不持有股票状态所得金钱一定比持有股票状态得到的多,那么返回值为dp[n-1][0];
4.确定遍历顺序
从递推公式可以看出dp[i]都是有dp[i - 1]推导出来的,那么一定是从前向后遍历
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(2, 0));
dp[0][1] = -prices[0];
dp[0][0] = 0;
for (int i = 1; i < prices.size(); i++) {
dp[i][1] = max(dp[i - 1][1], -prices[i]);
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
}
return dp[prices.size() - 1][0];
}
};
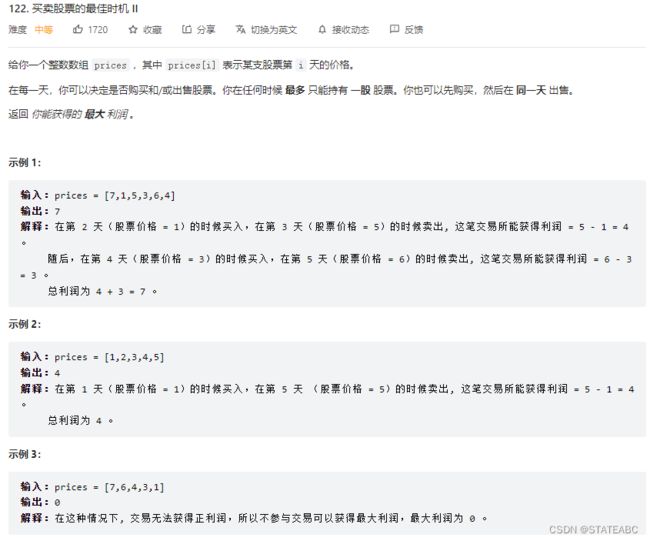
题目2:122.买卖股票的最佳时机Ⅱ(可以买卖多次)
1.确定dp数组以及下标的含义
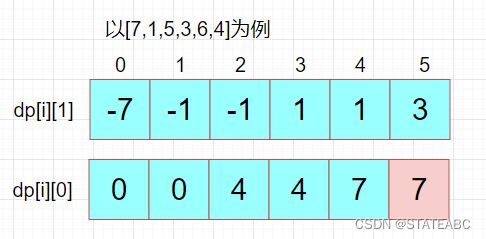
dp[i][0]表示第 i 天交易完后手里没有股票的最大利润
dp[i][1]表示第 i 天交易完后手里持有一只股票的最大利润(i从0开始)
2.确定状态转移方程
dp[i][0]的状态转移方程:
第i天不持有股票,那么有两种可能:①第i-1天就已经不持有股票了,即dp[i-1][0];②第i-1天时持有股票(即dp[i-1][1]),在第i天卖掉,即dp[i-1][1]+prices[i]。
那么dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1]的状态转移方程:
第i天持有股票,那么也有两种可能:①第i-1天已经持有了一支股票,即dp[i-1][1];②第i-1天不持有股票(即dp[i-1][0]),那么需要在第i天买入,即dp[i-1][0]-prices[i]。
那么dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
全部交易结束后,持有股票的收益一定低于不持有股票的收益,因此这时候 dp[n−1][0] 的收益必然是大于 dp[n−1][1] 的,最后的答案即为 dp[n−1][0]。
3.dp数组初始化
根据状态转移方程可得,
dp[0][0] = 0,dp[0][1] = -prices[0]
4.确定遍历顺序
从前往后遍历
class Solution {
public:
int maxProfit(vector<int>& prices) {
vector<vector<int>> dp(prices.size(), vector<int>(2));
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < prices.size(); ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[prices.size() - 1][0];
}
};
可以看出,121和122唯一的区别就在于状态转移公式
题目3:123.买卖股票的最佳时机Ⅲ(最多买卖两次)
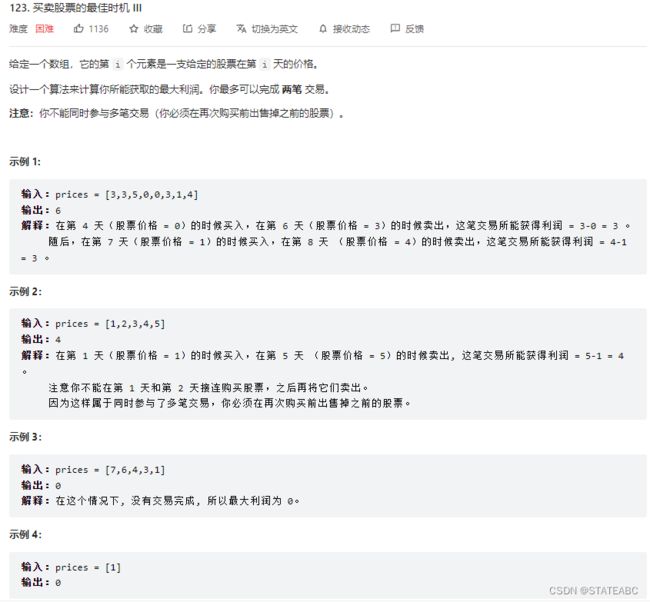
本题相对于前面两题反而难了一些,主要是在于最多买卖两次,那么就有了:不进行买卖、买卖一次、买卖两次
1.确定dp数组以及下标的含义
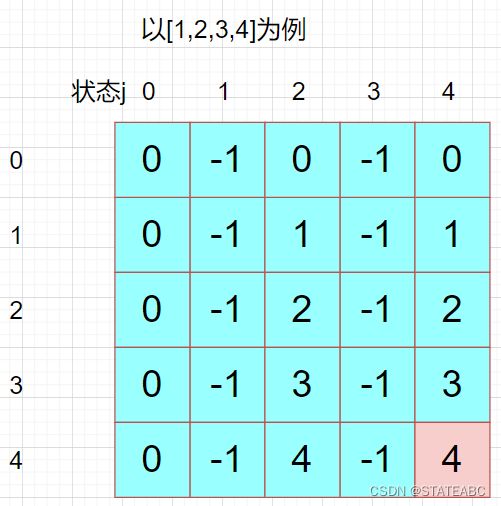
根据前边提到的三种买卖,一天结束后会有五个状态:0.没有操作;1.第一次买入;2.第一次卖出;3.第二次买入;4.第二次卖出
用dp[i][j]表示第 i 天交易完状态 j 所得到的最大利润
dp[i][1]、dp[i][3],表示的是第 i 天,买入股票的状态,并不是说一定要第 i 天买入股票,也可能前一天买入的,今天只是保持了昨天的买入状态。
当然也有题解用dp[i][j][0/1]表示第i天交易完,j次交易(买入/卖出)股票后,持有/不持有时的最大利润。
2.确定状态转移方程
如果第 i 天没有任何操作,那么就和i-1天相同, dp[i][0] = dp[i-1][0]。
如果第 i 天第一次买入股票即dp[i][1], 可以由两个状态推出来:
第 i-1 天就买入股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][1];
第 i 天买入股票(第 i 天买入了代表第 i 天买入股票),说明前一天是没有任何操作的状态因此所得现金就是前一天没有任何操作剩下的钱减去今天买入的股票后所花的现金即:dp[i-1][0] - prices[i];
那么dp[i][1]应该选所得现金最大的,所以dp[i][1] = max(dp[i - 1][1] , dp[i-1][0] - prices[i])。
如果第 i 天第一次卖出股票即dp[i][2], 可以由两个状态推出来:
第 i-1 天就卖出股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][2];
第 i 天卖出股票(第 i 天买入了代表第 i 天买入股票),所得现金就是前一天买入股票剩余的钱加上今天卖出的股票后所得现金即:dp[i-1][1] + prices[i];
那么dp[i][2]应该选所得现金最大的,所以dp[i][2] = max(dp[i - 1][2] , dp[i-1][1] + prices[i])。
同理,dp[i][3] = max(dp[i - 1][3] , dp[i-1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4] , dp[i-1][3] + prices[i]);
3.dp数组初始化
第0天没有操作dp[0][0],即:dp[0][0] = 0;
第0天做第一次买入的操作dp[0][1],dp[0][1] = -prices[0];
第0天做第一次卖出的操作dp[0][2],股票买卖最差情况也就是没有盈利即全程无操作现金为0,因此dp[0][2] = 0;
同理dp[0][3] = -prices[0]、dp[0][4] = 0;
最大的利润值为最后一次卖出即 dp[prices.size()-1][4];
4.确定遍历顺序
从前向后遍历,因为dp[i]依靠dp[i - 1]的数值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
dp[0][1] = -prices[0], dp[0][3] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[prices.size() - 1][4];
}
};
题目4:188.买卖股票的最佳时机Ⅳ(最多买卖k次)

最多买卖两次时,会有22+1种状态,而最多买卖k次时,就会有2k+1种状态
1.确定dp数组以及下标的含义
一天结束后会有2*k+1种状态:
0.没有操作;
1.第一次买入;
2.第一次卖出;
3.第二次买入;
4.第二次卖出;
…
规律就是除0以外,偶数操作卖出、奇数操作买入
那么就可以用dp[i][j]表示第 i 天交易完状态 j 所得到的最大利润
2.确定状态转移方程
那么状态转移方程就可以根据dp数组的规律得出了,公式的推导和123是一样的
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
3.dp数组初始化
dp[0][0] = 0,表示第0天没有操作;
dp[0][1] = -prices[0],代表第0天第一次买入操作;
dp[0][2] = 0,代表第0天第一次卖出操作;
其他同理,买入时减去prices[i],卖出时最小利润为0
4.确定遍历顺序
从前向后遍历
5.举例推导dp数组
同123
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
for (int i = 1;i < prices.size(); i++) {
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[prices.size() - 1][2 * k];
}
};
题目5:309.最佳买卖股票时机含冷冻期(买卖多次,卖出有一天冷冻期)

这一题的题解众多,重点在于冷冻期的理解:在第 i 天卖出,那么 i+1 天就是冷冻期
1.确定dp数组以及下标的含义
dp[i][0]表示第 i 天结束,持有股票时的最大利润
dp[i][1]表示第 i 天结束,不持有股票 且 处于冷冻期的最大利润
dp[i][2]表示第 i 天结束,不持有股票 且 不处于冷冻期的最大利润
注意这里的时间是 第 i 天结束
2.确定状态转移方程
对于 dp[i][0],
目前持有的这一支股票可以是在第 i−1 天就已经持有的,即dp[i−1][0];
或者是第 i 天买入的,那么第 i−1 天就不能持有股票并且不处于冷冻期中,再减去买入股票的价格prices[i],即dp[i-1][2]-prices[i];
状态转移方程为:dp[i][0] = max(dp[i-1][0], dp[i-1][2] - prices[i])
对于dp[i][1],
在第 i 天不持有股票 且 处于冷冻期,说明在第 i-1 天持有股票并且在第 i 天卖掉了,即dp[i-1][0]+prices[i];
状态转移方程为:dp[i][1] = dp[i-1][0] + prices[i]
对于 dp[i][2],
在第 i 天结束之后不持有任何股票并且不处于冷冻期,说明当天没有进行任何操作,即第 i−1 天时不持有任何股票:如果i-1天处于冷冻期,对应的状态为 dp[i−1][1];如果i-1天不处于冷冻期,对应的状态为 dp[i−1][2]。
状态转移方程为:dp[i][2] = max(dp[i-1][1],dp[i-1][2])
3.dp数组初始化
dp[0][0] = -prices[0],dp[0][1] = 0,dp[0][2] = 0
4.确定遍历顺序
从前往后遍历
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> f(prices.size(), vector<int>(3));
f[0][0] = -prices[0];
for (int i = 1; i < prices.size(); ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][2] - prices[i]);
f[i][1] = f[i - 1][0] + prices[i];
f[i][2] = max(f[i - 1][1], f[i - 1][2]);
}
return max(f[prices.size() - 1][1], f[prices.size() - 1][2]);
}
};
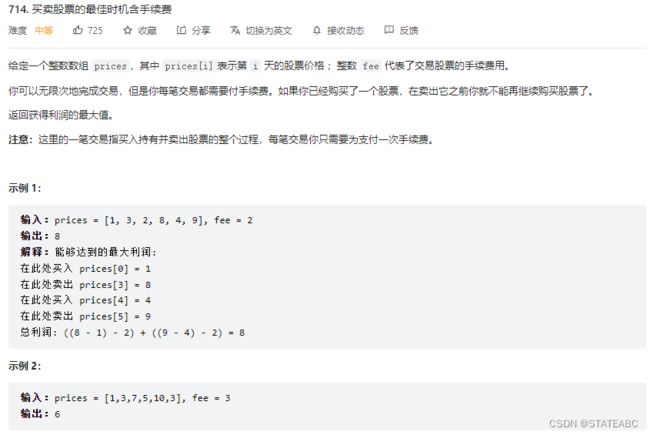
题目6:714.买卖股票的最佳时机含手续(买卖多次,每次由手续费)
class Solution {
public:
int maxProfit(vector<int>& prices,int fee) {
vector<vector<int>> dp(prices.size(), vector<int>(2));
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < prices.size(); ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[prices.size() - 1][0];
}
};