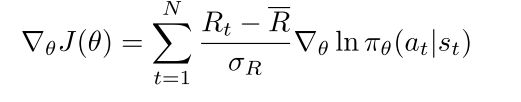Trajectory Simplification with Reinforcement Learning

Trajectory Simplification with Reinforcement Learning

轨迹数据是一种数据类型，用于捕捉移动物体的轨迹，如车辆、行人、机器人等。它是许多应用的核心，如城市流动性分析，物流，交通，体育比赛[1]等。轨迹数据通常是连续生成的，并由GPS设备等远程传感器收集。一个典型的场景是，传感器周期性地检查坐标和时间，这些坐标和时间对应于一个有时间标记的位置(称为时空点或简单的点)，并将这个点存储在缓冲区中。通常，传感器的存储预算较小，计算能力较低，网络带宽有限。随之而来的问题是缓冲区会频繁被占用，传输点的工作量会很大。此外，在某些应用中，可能会有数十万个传感器同时收集轨迹数据。一旦所有这些传感器收集到的轨迹数据在一个服务器上积累起来，其数量将是巨大的，这已经由几个现有的研究说明(见调查文件[2])。随之而来的问题是，轨迹数据的巨大容量增加了存储成本，更重要的是使数据的查询处理变得昂贵。解决上述两个问题的一种常见做法是进行轨迹简化，即在给定的轨迹上去掉一些点，保留其余的点作为简化轨迹。特别是在线模式

在批处理模式下，轨迹数据一次完整输入，在整个轨迹简化过程中保持可访问性。轨迹简化背后的基本原理是双重的。首先，轨迹上并非所有点都携带等量的信息，有些点只携带很少的信息，甚至不携带信息。例如，当一个物体以恒定的速度沿直线运动时，除第一个和最后一个点外，所有点都不携带信息，可以丢弃。其次，随着某些点的减少，传输、存储和查询处理的负担将显著降低。本文考虑了一个轨迹简化问题，即至少减少一定数量的点(或等价于最多保持一定数量的点)，以使作为简化轨迹误差的信息损失最小化。我们称这个问题为最小错误。

针对在线模式下的轨迹简化问题，提出了一种强化学习(RL)方法。我们将轨迹简化问题(在线模式下)视为一个顺序决策过程，即，它顺序地扫描轨迹，当缓冲区满时，它决定掉哪个点。过程模拟为马尔可夫决策过程，通过广泛使用的策略梯度方法[6][8]学习用于马尔可夫决策过程的策略，并开发了一种基于学习策略的轨迹简化方法。我们将此方法称为RLTS。与现有算法相比，RLTS算法计算的轨迹简化后误差更小，这主要是因为该算法具有数据驱动特性，并且能够适应输入点的不同动态特性

我们还提出了RLTS的一种变体，称为RLTS- skip，通过使用跳过被扫描点的额外操作来增强MDP。其基本原理是，有些点可能携带很少的信息，因此可以立即删除它们，而不必像RLTS那样在扫描时插入缓冲区。这样做的好处是，为跳过的这些点决定和采取行动的努力被节省了，效率也提高了。此外，RLTSSkip接受一个参数J，它控制允许跳过的最大点数。因此，RLTS- skip通过J的不同设置在效率和有效性之间提供了一种可调的平衡。注意，当J = 0时，RLTS- skip减少为RLTS。

随着数据访问的增加，我们有更多的选项来定义MDP的状态。我们研究了捕获轨迹点不同部分的三种状态定义，并相应地开发了三种不同类型的算法，即(1)RLTS和RLTS- skip， (2) RLTS+和RLTS- skip +， (3) RLTS++和RLTS- skip ++。RLTS和RLTS- skip与在线模式的状态完全相同，在线模式的底层状态是根据仅存储在缓冲区中的这些点定义的。RLTS+和RLTS- skip +分别是RLTS和RLTS- skip的增强版本，其中它们的状态是根据所有被扫描的点(包括那些存储在缓冲区中的点和那些被删除的点)定义的。此外，RLTS-Skip+通过扫描点后面的J点的信息进一步增加状态。RLTS++和RLTS- skip ++最终考虑了定义状态的所有点。从RLTS和RLTS- skip，到RLTS+和RLTS- skip +，再到RLTS++和RLTS- skip ++，捕获更多的信息来定义状态，相应地，mdp变得更加复杂，方法花费更多的时间

1.问题定义

(Min-Error): 给定一个轨迹和一个缓存，最小误差问题是找到一个简化的轨迹，使得能够满足缓存大小，同时满足在特定的误差范围内

2.ALGORITHMS FOR ONLINE MODE

我们将轨迹简化问题视为一个顺序决策过程，并将其建模为马尔可夫决策过程(MDP)[35](章节IV-A)，使用策略梯度方法[6][8]学习MDP的最优策略(章节IV-B)，然后开发一种称为RLTS的算法，它使用学习到的策略来解决最小错误问题(章节IV-C)。在第四节- d中，我们介绍了RLTS的一种变体，称为RLTS- skip，它通过跳过一些被扫描点来提高RLTS的效率。

2.1 Min-Error Modeled as an MDP

们将Min-Error问题建模为MDP，它由四个组件组成，即状态、操作、转换和奖励，如下所述

1)状态:假设有一个W点ps1, ps2，…，缓冲中的W个点和一个新输入的点pi将被插入到下一个缓冲区。任务是从缓冲区中删除一个点，然后插入这个点

2) Actions 我们定义了一个包含k个动作的动作空间，每一个动作意味着去掉一个点pπ(j)。形式上，我们定义了一个动作，用a表示

3) Transitions

4) Rewards  假设我们在一个状态下执行一个动作，然后我们到达一个新的状态。我们定义了与从状态s到状态s的转换相关的奖励，用r表示，如下所示。在状态s时，我们在缓冲区中有W个点，并且要插入一个新点pi。我们考虑缓冲器中的这些点，它们构成的轨迹与目前输入的轨迹的简化轨迹相对应

2.2 Policy Learning on the MDP

MDP的核心问题是为agent找到一个最优策略，该策略对应于一个函数，该函数指定agent在某一特定状态下应选择的行为，以使累计收益最大化。我们通过策略梯度(PNet)方法学习MDP的策略。PNet将随机策略拟合为πθ(a|s)，表示选择行为a的概率。PNet参数化πθ(a|s)使用神经网络如下 πθ(a|s) = σ(Ws + b)。然后，PNet计算出在参数θ下性能测度的梯度

The RLTS Algorithm

我们的RLTS算法是基于学习策略的MDP模型的最小误差问题

The RLTS-Skip Algorithm

在RLTS算法中，每个点被扫描后确定插入到缓冲区中。当扫描以下一些点时，它可能会被删除。因此，当扫描每个点时，需要通过RLTS中的神经网络来决定要删除缓冲区中的哪个现有点。虽然这种策略让每个点都有机会被包含在缓冲区中，从而探索可能简化轨迹的大空间，但它可能过于保守。

考虑这样一个场景，最近被扫描的点构成了一条轨迹，表明沿着一条带有常数的直线运动。在这个场景中，我们有足够的信心在一行中删除一定数量的点，而不是将它们一个一个地包含到缓冲区中，然后在后面的阶段删除它们中的一些。这将有助于节省扫描这些点时的决定和采取行动的努力，同时也不会对效率产生太大影响。

源码：https://github.com/zhengwang125/RLTS