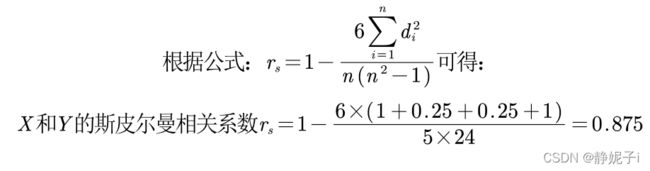数学建模算法学习
清风数学建模
综合评价问题
1.1 层次分析法AHP
1.2 TOPSIS法
1.3 模糊综合评价(国内比赛用的比较多,暂时不看)
数据处理
2.1 插值算法
2.2 拟合算法
相关性分析
3.1 皮尔逊相关系数
3.2 斯皮尔曼等级相关系数
3.3 典型相关性分析
图论
4.1 Dijkstra算法
4.2 Bellman Ford算法
回归分析
5.1 多元线性回归分析
系统分析问题
文章目录
- 清风数学建模
- 一、层次分析法
-
- 1.1层次分析法模型部分
-
- 层次分析法步骤:
- 层次分析法的局限性:
- 模型扩展
- 1.1层次分析法代码部分
- 二、TOPSIS法
-
- 2.1 TOPSIS法模型部分
-
- TOPSIS法步骤:
- 基于熵权法对TOPSIS模型的修正
-
- 熵权法的计算步骤:
- 2.2 TOPSIS法代码部分
- 三、插值算法
-
- 一维插值问题
- n维插值问题(了解)
- 插值方法用于短期预测但不建议
- 四、拟合算法
-
- 确定拟合曲线
- 求解拟合参数
-
- 最小二乘法
- 评价拟合函数
- 相关系数
-
- 相关概念(概率论)
- 皮尔逊相关系数的计算:
- 处理数据示例
-
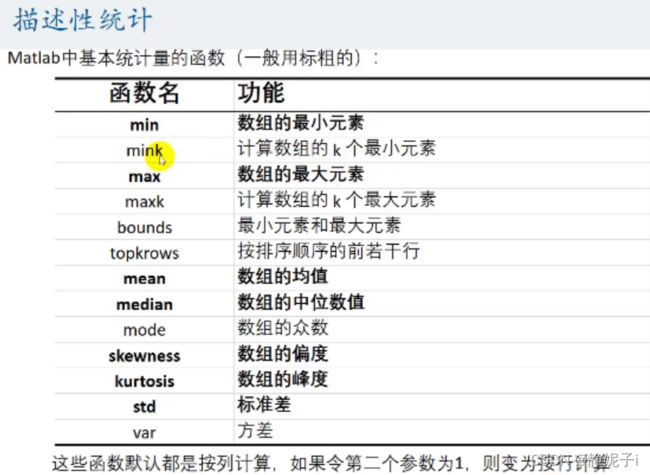
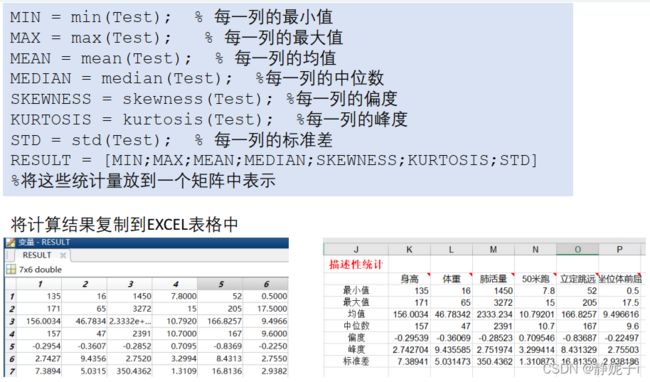
- 首先对数据进行描述性统计
- 计算皮尔逊相关系数
- 假设检验
-
- 假设检验步骤
- 皮尔逊相关系数假设检验的条件
-
- 检验数据是否是正态分布:
-
- 正态分布JB检验(大样本n>30)
- Shapiro-wilk夏皮洛-威尔克检验(小样本3<=n<=50)
- Q-Q图法(数据量非常大:成百上千个样本):
- 对皮尔逊相关系数进行假设性检验
- 斯皮尔曼相关系数(没有通过正态性检验的情况下)
-
-
- 斯皮尔曼相关系数的假设检验
-
- 比较与总结
- 典型相关分析(不太理解)
-
- 典型相关分析的定义
- 典型相关分析的思路
-
- 样本典型相关变量及典型相关系数
- 典型相关系数的显著性检验
- 举例说明
- 典型相关分析的拓展
-
- 从相关矩阵出发计算典型相关
- 典型载荷分析
- 典型冗余分析
- 典型相关分析关键步骤:
- 图论最短路
-
- 图的基本概念
- 单源最短路
- Dijkstra算法
- Bellman-Ford算法
- matlab计算最短路径
- 多源最短路
- Floyd算法
- 回归分析
-
- 回归分析概念
- 回归分析分类
- 回归分析任务
- 数据的分类
- 数据的收集
- 多元线性回归分析
-
- 一元线性回归
- 回归系数的解释
-
- 内生性的定义和度量
- 内生性的蒙特卡洛模拟
- 解决内生性的方法
- 回归系数的解释
- 四类模型回归系数的解释
- 特殊变量的处理:虚拟变量
- 举例进行回归分析
-
-
- 题目描述
- 使用软件
-
- 蒙特卡洛模拟
-
- 定义:
- 应用:
-
- 求解有约束的非线性规划问题
- 01规划问题
- 导弹追踪问题
- 旅行商问题
- 数学规划模型
-
- 概述
- 线性规划问题求解
- 线性规划典型例题
- 整数规划
-
- 整数规划的典型例题:
- 非线性规划问题
-
- matlab求解非线性规划
- 最大最小化模型
- 多目标规划模型
- 分类模型
-
- 逻辑回归
- Fisher线性判别分析
- 多分类问题
- 聚类问题
-
- K-means聚类算法
- 系统(层次)聚类
- 基于密度的聚类算法dbscan算法
- 时间序列分析
-
- 指数平滑模型
-
- simple模型
- 线性趋势模型
- 简单季节性模型
-
- 温特加法模型
- 温特乘法模型
- 时间序列建模过程
- 预测模型
一、层次分析法
1.1层次分析法模型部分
引入现实问题:
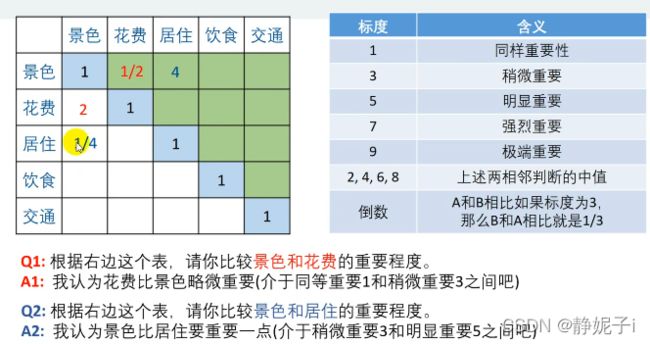
评价类问题可用打分解决,针对不同指标得到权重打分表(如下图),

“确定评价指标,形成评价体系,选择最佳方案”——>评价类问题
解决评价类问题的出发点:
- 评价目标
- 为达到目标的可选方案
- 评价准则/指标(自行分析)
一般而言,前两者显而易见,对于评价指标的分析需要我们根据题目中的背景材料,常识以及网上搜集到的参考资料进行结合,从中筛选出最合适的指标。
网络参考资料来源:优先知网,万方,百度学术等学术平台搜索相关文献(一个综合搜索平台:虫部落)
查询资料确定评价指标后,确定指标权重
不能直接主观地去分配权重:一次性考虑五个指标之间的关系,往往考虑不周。

解决方法:
两个两个指标进行比较,最终根据两两比较的结果推算出权重。
——层次分析法

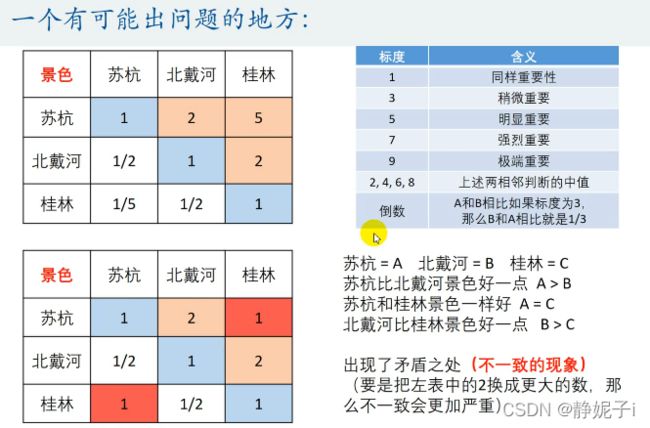
由于可能存在的不一致问题,故求得判断矩阵后一定要进行一致性检验
原理:检验我们构造的判断矩阵和一致矩阵是否有太大差别


一致性检验的步骤:
-
计算一致性指标CI
C I = λ m a x − n n − 1 CI = \frac{{\lambda}_{max}-n}{n-1} CI=n−1λmax−n -
计算一致性比例CR
C R = C I R I CR = \frac{CI}{RI} CR=RICI
(如果CR<0.1,可认为判断矩阵一致性可以接受,否则需要对判断矩阵进行修正)
![]()
方法一、算术平均法求权重
方法二、几何平均法求权重
方法三:特征值法求权重
一致矩阵特性:有一个特征值为n,其余特征值均为0


在比赛中,特征值法求判断矩阵权重较为常见,可利用代码快速求得
求得指标权重后即可填入权重矩阵,得到最终得分如下图

层次分析法步骤:
- 分析系统中各因素之间的关系,将决策的目标、考虑的因素(决策准则)和决策对象按照他们之间的相互关系分为目标层,准则层,方案层,建立系统的递阶层次结构如下:
(要放到论文中的!)

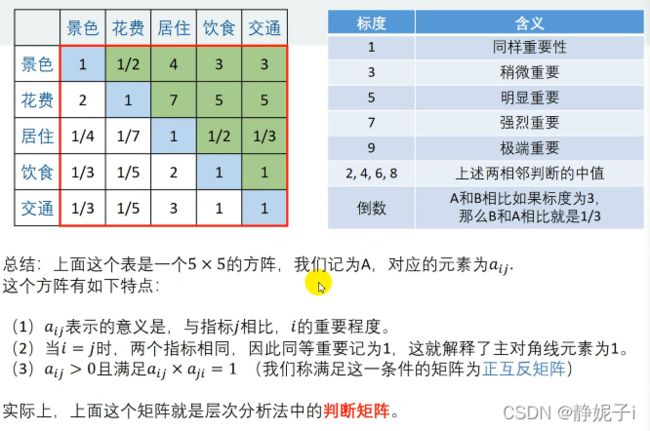
- 对于同一层次上的各元素关于上一层次中某一准则的重要性进行两两比较(采用相对尺度,以尽可能减少性质不同因素相互比较的困难,以提高准确度),构造两两比较矩阵(判断矩阵)

- 由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用)
有三种方法计算权重:(三种全用!)

- 计算各层元素对系统目标的合成权重,并进行排序
PS:可以通过流程图将方法步骤展现出来(简洁明了不易查重)例如:

层次分析法的局限性:
模型扩展
 对于准则层的指标有多个子指标的情况:
对于准则层的指标有多个子指标的情况:
将权重相乘得到子指标在总情况下的权重
1.1层次分析法代码部分
二、TOPSIS法
TOPSIS法:逼近理想解排序法又称优劣解距离法
一种常用的综合评价方法,能充分利用原始数据的信息,结果能精确反映各评价方案之间的差距。

2.1 TOPSIS法模型部分
问题引入:
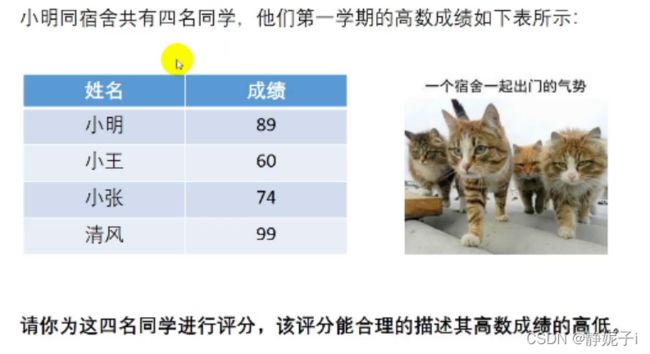
正常情况下,我们按照分数进行排名,排名高即排名数小,但是在这里要求的评分应当是排名高评分高,所以不可用寻常方式进行排名,我们需要对排名进行修正,如下进行了简单的倒序排列。
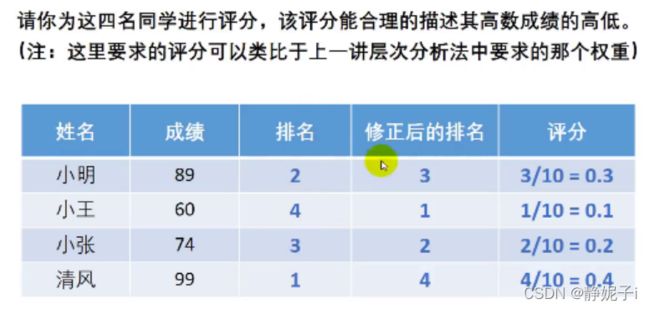
当分数变化时,保持相对排名不变,评分也不会变化
(考10分和考60分,能一样吗?!!)
用数学语言描述:
此评分不能充分反映原始数据的全部信息,虽然与成绩数据有一定的相关性,但相关性不是很强。
另一种评分方式:
 此种评分方式也不合适:
此种评分方式也不合适:
因为有很多指标不存在理论上的最大值和最小值,如GDP增速
(此例中的卷面成绩100,0也是特殊情况)
因此我们考虑令公式中的最大最小值为参考数据的极值,评分公式如下:
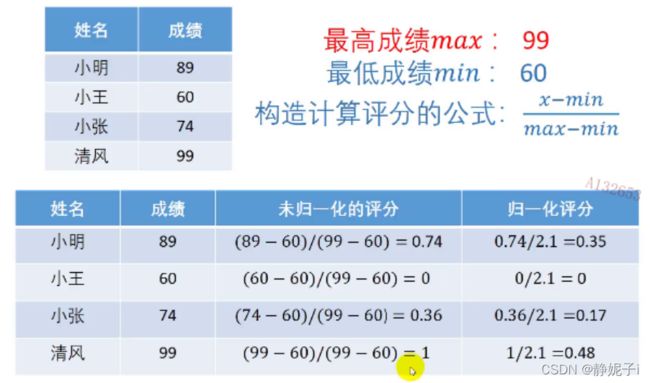
关于此评分公式正确性的三点解释:
- 比较对象一般远大于两个。(虽然极值处两点评分分别为0,1,数据相关性较低,无法充分反映极值点处的数据,但比较对象较多时,此类情况的误差可忽略不计)
- 比较的指标往往不只是一个方面的。(多方面评测指标情况下,单一方面极值带来的误差可忽略不计)
- 有很多指标不存在理论上的最大值和最小值(如GDP增速)
最终得到评分评价标准:

扩展问题:
增加指标个数

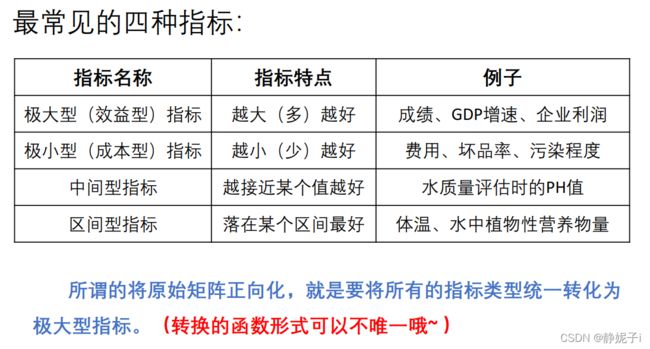
在新问题中,评价指标可分为极大型指标和极小型指标
当我们需要对其进行综合评价时,需要统一标准,即进行指标正向化。
![]() 但不同评价指标的量纲不同,不能进行直接进行简单的加和
但不同评价指标的量纲不同,不能进行直接进行简单的加和
因此我们需要对指标进行标准化如下:
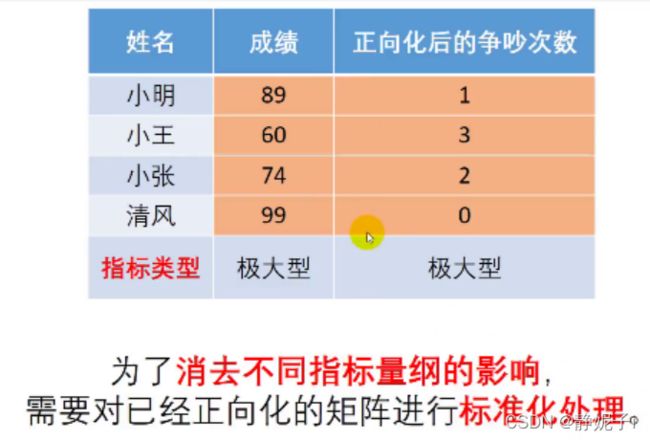
标准化处理计算公式:
 得到统一标准的指标评分如下:
得到统一标准的指标评分如下:
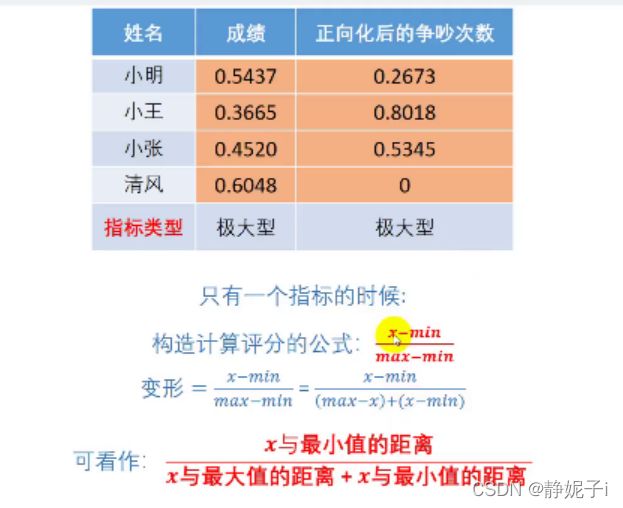 欧式距离计算得分
欧式距离计算得分
 带入此问题计算可得:
带入此问题计算可得:
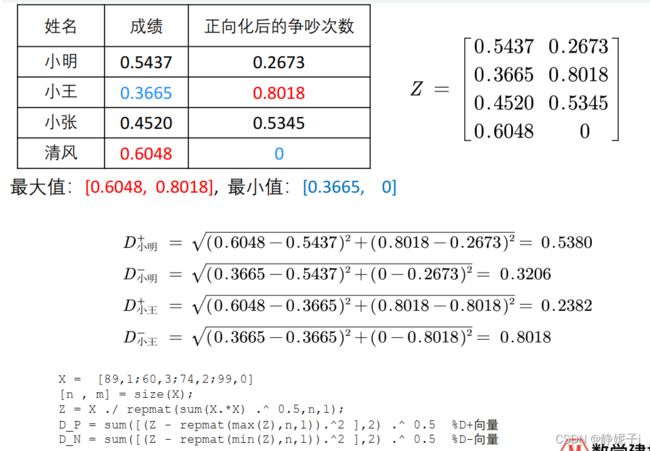 对评分计算结果进行归一化:
对评分计算结果进行归一化:
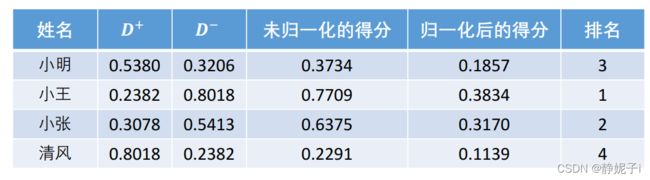
TOPSIS法步骤:
- 将原始矩阵正向化
基于熵权法对TOPSIS模型的修正

之前我们都是利用层次分析法对评价指标的权重进行计算,但这种方法的主观性过强,对结果产生较大影响。因此我们引入一种客观赋权方法。
熵权法:是一种客观赋权方法。
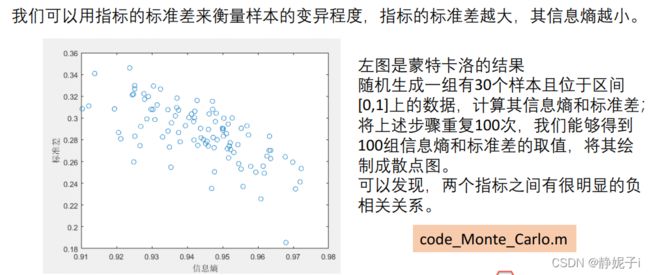
依据原理:指标的变异程度越小,所反映的信息量也越少,其对应的权值也应该越低。(客观=数据本身就可以告诉我们权重)
一个极端例子:对于所有样本而言,这个指标都是相同的数值,那么我们可认为这个指标的权值为0,即这个指标对于我们的评价起不到任何帮助)
对于信息量大小的度量:
越有可能发生的事情,信息量越少,
越不可能发生的事情,信息量就越多。
怎么衡量事情发生的可能性大小?概率
小张和小王是两个高中生。小张学习很差,而小王是全校前几名的尖子生。高考结束后,小张和小王都考上了清华。小王考上了清华,大家都会觉得很正常,里面没什么信息量,因为学习好上清华,天经地义,本来就应该如此的事情。
然鹅,如果是小张考上了清华,这就不一样了,这里面包含的信息量就非常大。怎么说?因为小张学习那么差,怎么会考上清华呢?把不可能的事情变成可能,这里面就有很多信息量。
注:本例子来自微信公众号:“小宇治水 ”
定义概率与信息量的函数关系:
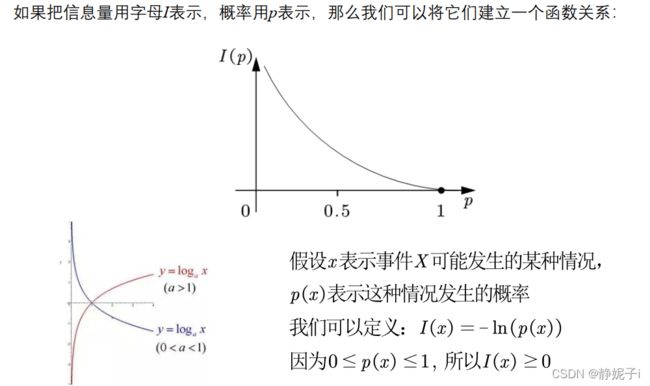


对于熵权法而言,我们关注的是已有信息,因此信息熵越大,信息量越小。
熵权法的计算步骤:
- 判断输入的矩阵中是否存在负数,如果有则要重新标准化到非负区间(后面计算概率时需要保证每一个元素为非负数)

- 计算第j项指标下第i个样本所占的比重,并将其看作相对熵计算中用到的概率

- 计算每个指标的信息熵,并计算信息效用值,并归一化得到每个指标的熵权

2.2 TOPSIS法代码部分
导入数据(.mat)
load ***.mat
第一步:原始矩阵正向化:
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标'])
Judge = input(['指标是否需要正向化处理,1(需要) ,0(不需要): ']);
if Judge == 1
loc = input('需要正向化处理的指标(列数): ');
type = input('需要处理的指标类型(1:极小型, 2:中间型, 3:区间型): ')
%两个同纬度的行向量
for i = 1 : size(loc,2)
%对这些列分别处理,循环次数:列数
X(:,loc(i)) = Positivization(X(:,loc(i)),type(i),loc(i));
% 按输入顺序选择需要正向化处理的某一列向量X(:,loc(i))
% 使用Positivization函数,对选出的指标评分进行正向化,其参数包括需要处理的(列向量),需要处理的指标类型,列数
% 返回正向化之后的指标,直接赋值给我们原始数据
end
disp('正向化后的矩阵 X = ')
disp(X)
end
正向化处理函数:
% function [输出变量] = 函数名称(输入变量)
% 函数的中间部分都是函数体
% 函数的最后要用end结尾
% 输出变量和输入变量可以有多个,用逗号隔开
% function [a,b,c]=test(d,e,f)
% a=d+e;
% b=e+f;
% c=f+d;
% end
% 自定义的函数要单独放在一个m文件中,不可以直接放在主函数里面(和其他大多数语言不同)
function [posit_x] = Positivization(x,type,i)
% 输入变量有三个:
% x:需要正向化处理的指标对应的原始列向量
% type: 指标的类型(1:极小型, 2:中间型, 3:区间型)
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示:正向化后的列向量
if type == 1 %极小型
disp(['第' num2str(i) '列是极小型,正在正向化'] )
posit_x = Min2Max(x); %调用Min2Max函数来正向化
disp(['第' num2str(i) '列极小型正向化处理完成'] )
elseif type == 2 %中间型
disp(['第' num2str(i) '列是中间型'] )
best = input('请输入最佳的那一个值: ');
posit_x = Mid2Max(x,best);
disp(['第' num2str(i) '列中间型正向化处理完成'] )
elseif type == 3 %区间型
disp(['第' num2str(i) '列是区间型'] )
a = input('请输入区间的下界: ');
b = input('请输入区间的上界: ');
posit_x = Inter2Max(x,a,b);
disp(['第' num2str(i) '列区间型正向化处理完成'] )
else
disp('没有这种类型的指标,请检查Type向量中是否有除了1、2、3之外的其他值')
end
end
function [posit_x] = Inter2Max(x,a,b)
r_x = size(x,1); % row of x
M = max([a-min(x),max(x)-b]);
posit_x = zeros(r_x,1); %zeros函数用法: zeros(3) zeros(3,1) ones(3)
% 初始化posit_x全为0 初始化的目的是节省处理时间
for i = 1: r_x
if x(i) < a
posit_x(i) = 1-(a-x(i))/M;
elseif x(i) > b
posit_x(i) = 1-(x(i)-b)/M;
else
posit_x(i) = 1;
end
end
end
function [posit_x] = Mid2Max(x,best)
M = max(abs(x-best));
posit_x = 1 - abs(x-best) / M;
end
function [posit_x] = Min2Max(x)
posit_x = max(x) - x;
%posit_x = 1 ./ x; %如果x全部都大于0,也可以这样正向化
end
第二步:对正向化后的矩阵进行标准化:
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)
第三步:计算得分
%% 计算与最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')
% sort(A)若A是向量不管是列还是行向量,默认都是对A进行升序排列。sort(A)是默认的升序,而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵,默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A)
% dim=2时表示对A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中给一维向量排序是使用sort函数:sort(A),排序是按升序进行的,其中A为待排序的向量;
% 若欲保留排列前的索引,则可用 [sA,index] = sort(A,'descend') ,排序后,sA是排序好的向量,index是向量sA中对A的索引。
% sA = 8 3 2 1
% index = 4 3 1 2
三、插值算法
当现有数据较少不足以支撑分析的进行时,需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满足需求。
一维插值问题
上面讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值,而这种插值多项式却不能全面反映被插值函数的性态。
然而在许多实际问题中,不仅要求插值函数与被插值函数在所有节点处有相同的函数值,它也需要在一个或全部节点上插值多项式与被插
函数有相同的低阶甚至高阶的导数值。
对于这些情况,拉格朗日插值和牛顿插值都不能满足
龙格现象(Runge):
高次插值会产生龙格现象,即在两端处波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下,不要轻易使用高次插值。
由于插值多项式次数高精度未必显著提高,反而摄入误差可能会显著增大,为了提高插值精度,我们需要采取分段低次插值。
分段插值
 最为常用的两种方法
最为常用的两种方法
分段三次埃尔米特插值

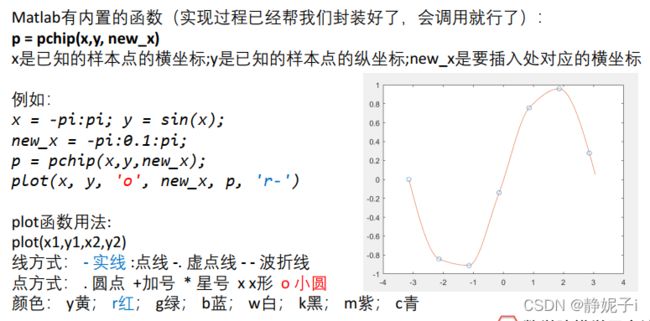 三次样条插值
三次样条插值



n维插值问题(了解)
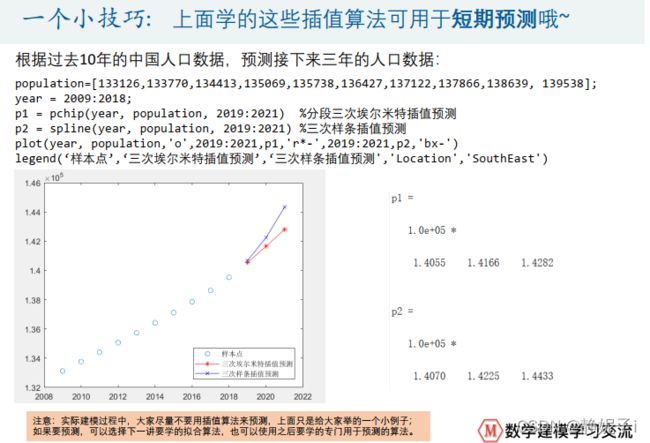
插值方法用于短期预测但不建议
四、拟合算法
与插值问题不同(插值算法中,得到的多项式f(x)要经过所有样本点。但是如果样本点太多,那么这个多项式次数过高,会造成龙格现象,尽管我们可以选择分段的方法避免这种现象,但分段函数形式复杂)
在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个确定的函数(曲线),使得该曲线在某种准则下(只要保证误差足够小)与所有的数据点最为接近,即曲线拟合的最好(最小化损失函数)。
确定拟合曲线
首先根据样本点的分布,确定拟合曲线类型,再进一步求解参数,例如:线性关系

求解拟合参数
最小二乘法
评价拟合函数
SSE越小越好(会受量纲的影响)
——>用拟合优度解决这个问题




在函数中,参数仅以一次方出现,且不能乘以或除以其他任何参数,不能出现参数的复合函数形式。
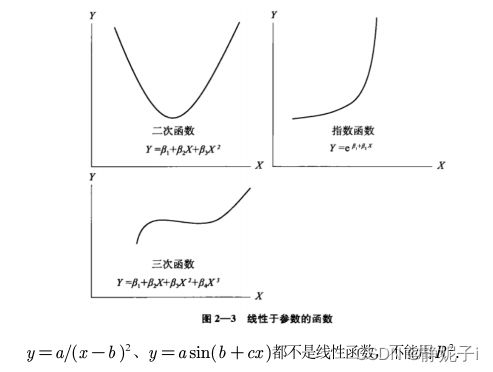 matlab曲线拟合工具箱:
matlab曲线拟合工具箱:
curve fitting(导出图片会更高清,还可以生成代码)

SSE(和方差、误差平方和):The sum of squares due to error
MSE(均方差、方差):Mean squared error
RMSE(均方根、标准差):Root mean squared error
R-square(确定系数):Coefficient of determination
Adjusted R-square:Degree-of-freedom adjusted coefficient of determination
相关系数
两种常用相关系数:皮尔逊相关系数,斯皮尔曼等级相关系数
用于衡量两个变量之间相关性的大小,根据数据满足的不同条件,选择不同的相关系数进行计算和分析(但是最容易用错的方法)
相关概念(概率论)
总体——所要考察对象的全部个体叫做总体.
希望得到总体数据的一些特征(例如均值方差等)
样本——从总体中所抽取的一部分个体叫做总体的一个样本.
计算这些抽取的样本的统计量来估计总体的统计量:
用样本估计总体:例如使用样本均值、 样本标准差来估计总体的均值(平均水平)和总体的标准差(偏离程度) 。
皮尔逊相关系数的计算:
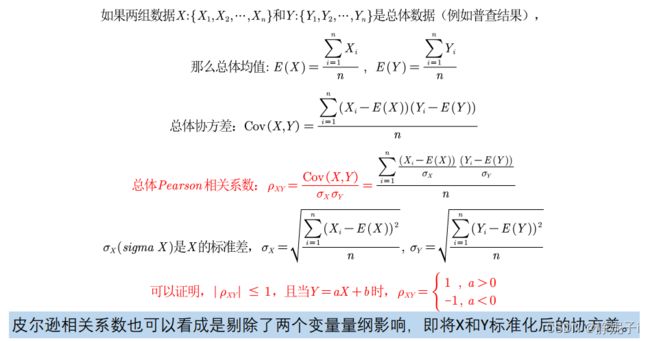
 相关系数只是用来衡量两个变量线性相关程度的指标
相关系数只是用来衡量两个变量线性相关程度的指标
即:先确认两个变量的线性相关关系,然后才能通过相关系数表现变量之间的相关程度。
(先画散点图观察线性相关性)
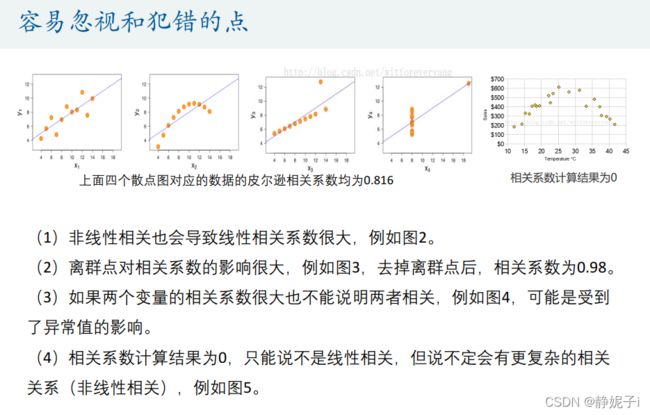 Conclusion:
Conclusion:
- 如果两个变量本身就是线性的关系,那么皮尔逊相关系数绝对值大的就是相关性强,小的就是相关性弱。
- 在不确定两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,需要画出散点图结合图像观察变量相关性。
处理数据示例
首先对数据进行描述性统计
计算皮尔逊相关系数
计算6个变量两两之间的关系:
使用SPSS简化操作:
 matlab计算相关系数
matlab计算相关系数
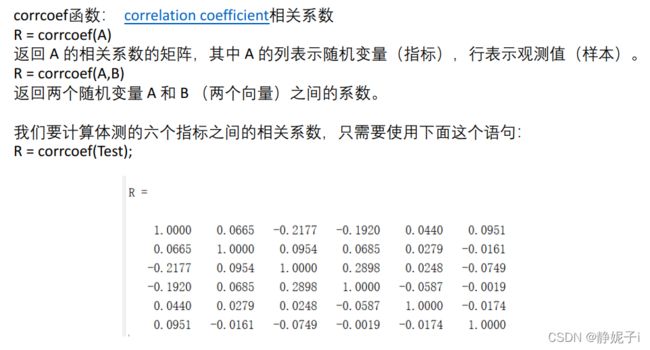
并可视化成好看的图表放在论文中。
假设检验
假设检验定义
为了判断样本与样本,样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。
假设检验的假设
由定义可知,我们需要对结果进行假设,然后拿样本数据去验证这个假设。
所以做假设检验时会设置两个假设:
一种叫原假设,也叫零假设,用H0表示。原假设一般是统计者想要拒绝的假设。
另外一种叫备择假设,用H1表示。备则假设是统计者想要接受的假设。
假设检验的基本原理
(1)先假设总体某项假设成立,计算其会导致什么结果产生。若导致不合理现象产生,则拒绝原先的假设。若并不导致不合理的现象产生,则不能拒绝原先假设,从而接受原先假设。(相信原假设成立的概率:置信水平 β = 1 − α \beta=1-\alpha β=1−α,一般95%)
(2)它又不同于一般的反证法。所谓不合理现象产生,并非指形式逻辑上的绝对矛盾,而是基于小概率原理:概率很小的事件在一次试验中几乎是不可能发生的,若发生了,就是不合理的。至于怎样才算是“小概率”呢?通常可将概率不超过0.05的事件称为“小概率事件”,也可视具体情形而取0.1或0.01等。
在假设检验中常记这个概率为α,称为显著性水平。而把原先设定的假设成为原假设,记作H0。把与H0相反的假设称为备择假设,它是原假设被拒绝时而应接受的假设,记作H1。
假设检验步骤
例:小明称体重发现自己94斤,以前都是90斤,现在想检验:这个月体重是否仍为90斤(体重W)或者说这个月体重和90斤有无显著差异。
第一步:确定原假设H0和备择假设H1
(H0和H1是恰好相反的两面)
H0: W=90;H1:W!=90
H1——>W>90 or W<90 ——>双侧检验(单方面的:单侧检验)
第二步:在原假设H0成立的条件下,根据我们要检测的量构造一个分布(标准正态,t分布,F分布,卡方分布)
H0:W=90——>W~N(90,4)
正态分布标准化: W − 90 2 ∽ N ( 0 , 1 ) {\frac {W-90} 2 }\backsim~N(0,1) 2W−90∽ N(0,1)
Z= W − 90 2 {\frac {W-90} 2 } 2W−90:统计量(只能够包含一个未知量,记为Z)
第三步:画出分布的概率密度图
给一个置信水平 β \beta β(相信H0成立的概率),求出接受域范围即P(a<=统计量<=b)= β \beta β
【一般 β = 90 % , 95 % , 99 % \beta=90\%,95\%,99\% β=90%,95%,99%(95用的最多)】
(可以去概率论复习该部分内容)

第四步:用已知的样本数据带入计算统计量,得到检验值,若检验值落在[a,b]内,将无法拒绝原假设,否则拒绝原假设

得到结果:H0有问题
皮尔逊相关系数假设检验的条件
第一, 实验数据通常假设是成对的来自于正态分布的总体。 因为我们在求皮尔逊相关性系数以后,通常还会用t检验之类的方法来进行皮尔逊相关性系数检验,而t检验是基于数据呈正态分布的假设的。
第二, 实验数据之间的差距不能太大。 皮尔逊相关性系数受异常值的影响比较大。
第三:每组样本之间是独立抽样的。 构造t统计量时需要用到。
事实上:2,3点可以默认满足,第一个条件需要我们进行验证。
检验数据是否是正态分布:
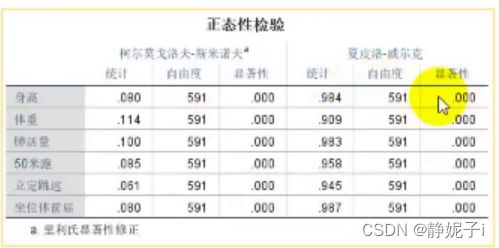
正态分布JB检验(大样本n>30)
Shapiro-wilk夏皮洛-威尔克检验(小样本3<=n<=50)
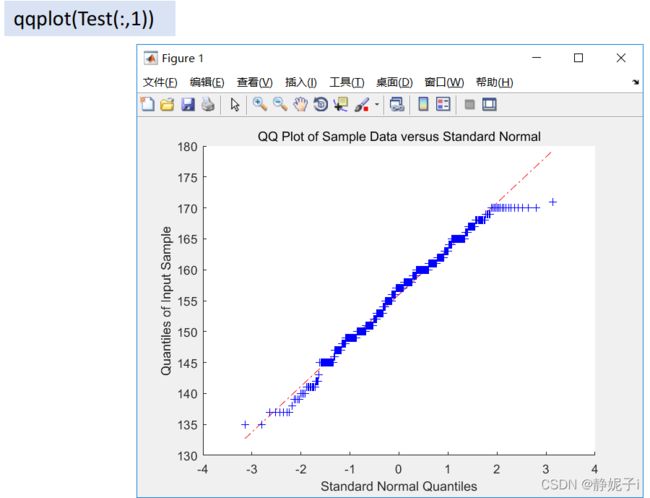
Q-Q图法(数据量非常大:成百上千个样本):
对皮尔逊相关系数进行假设性检验

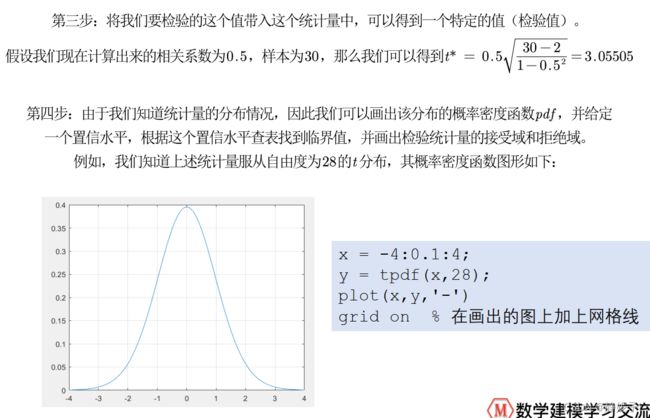

 更简便的方法:计算p值
更简便的方法:计算p值
 *的作用:
*的作用:
0.5:不显著
0.5*:在90%的置信水平上显著
0.5**:在95%的置信水平上相关系数显著地异于0
0.5***:99%
matlab计算相关系数及p值:
导出相关系数并标注上显著性水平
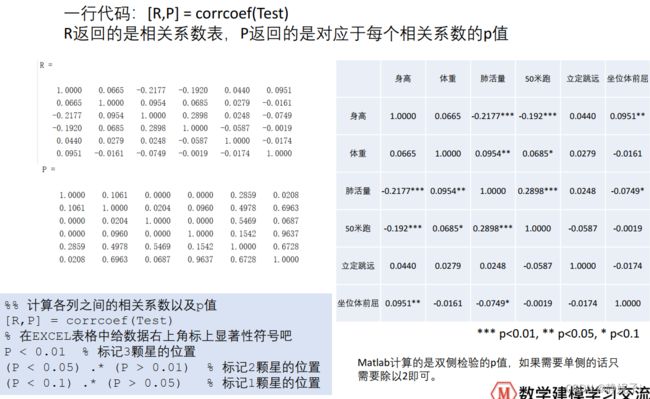 (还可以用SPSS简化操作:分析——相关——双变量选中指标——选择皮尔逊相关系数,双尾(双侧检验),选中标记显著性,相关性)
(还可以用SPSS简化操作:分析——相关——双变量选中指标——选择皮尔逊相关系数,双尾(双侧检验),选中标记显著性,相关性)
快速得到标注了显著性的相关信息表
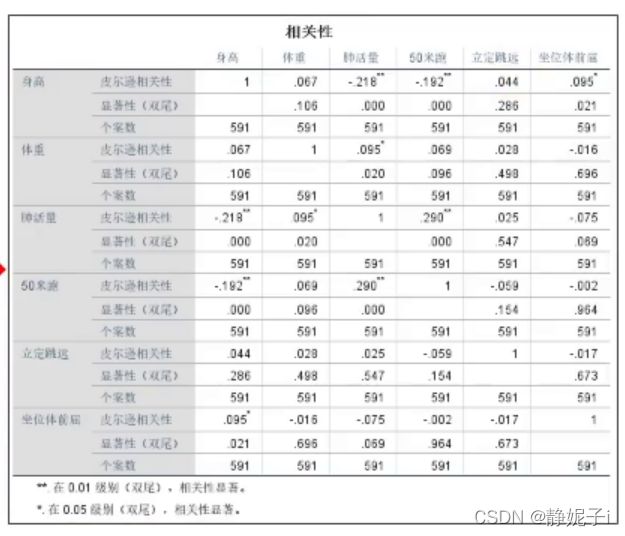
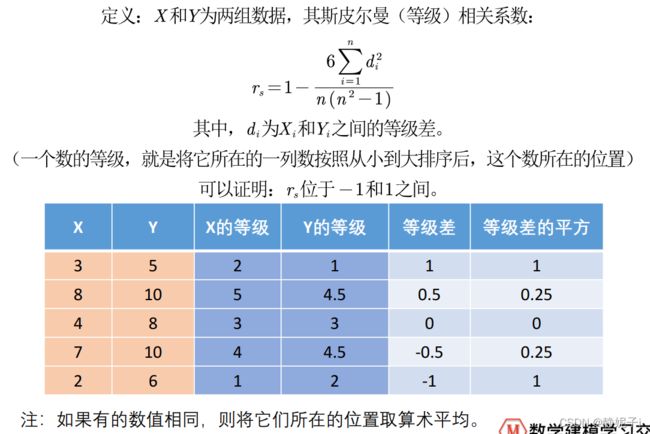
斯皮尔曼相关系数(没有通过正态性检验的情况下)
斯皮尔曼相关系数的假设检验
比较与总结
典型相关分析(不太理解)
研究两组变量(每组变量中可能有多个指标)之间相关关系的一种多元统计方法,可以揭示出两组变量之间的内在联系。
直接对这些变量的相关进行两两分析,很难得到关于这两组变量(观众和业内人士)之间关系的一个清楚的印象。
——>把多个变量与多个变量之间的相关化为两个具有代表性的变量之间的相关。
代表性指标: 能较为综合、全面的衡量所在组的内在规律。
一组变量最简单的综合形式就是该组变量的线性组合
典型相关分析的定义
CCA典型相关分析(canonical correlation analysis)
利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。
它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
相关性被提取完毕——>假设性检验:不显著
典型相关分析的思路
X(Xi列向量),p,q代表组内指标个数
第一组变量代表U,第二组变量代表V
a,b分别是第1,2组变量线性组合的系数矩阵
若一组U,V反映的样本信息不够,需要再找一组,且两组总和变量信息不相关:
cov(U1,U2)=cov(V1,V2)=0
在方差等于1的前提下,使得代表的相关系数最大,则此代表就是原始数据的第一对典型变量,其系数为第一典型系数,——>再求互不相关的第二对,第三对…这些典型相关变量刻画了原始两组数据之间的线性相关性,后续还需要对相关系数进行显著性检验,不显著的典型相关变量没有意义可以忽略。
样本典型相关变量及典型相关系数
写论文时,若用到典型相关分析,应当先给出假设:数据服从正态分布
典型相关系数的显著性检验
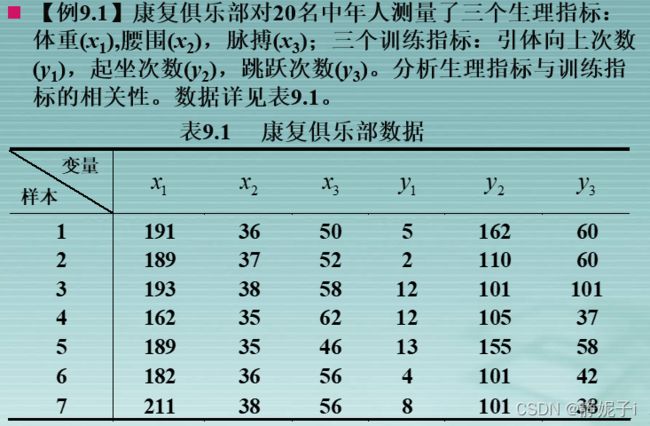
举例说明
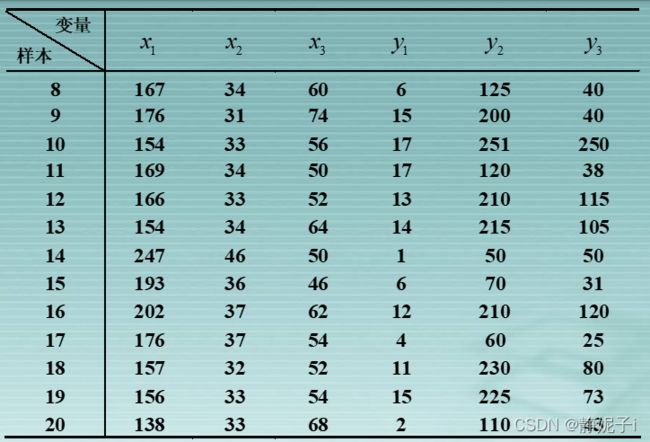
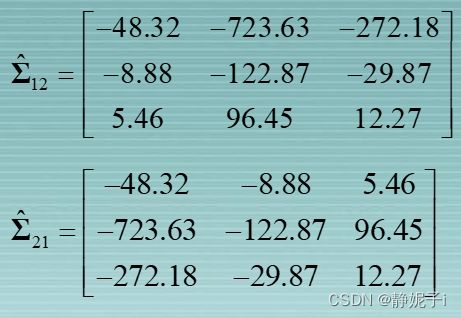
利用样本数据对协方差矩阵进行估计如下
根据协方差矩阵计算得到A,B矩阵估计值
求出A,B矩阵的非0特征值,开根号得到典型相关系数如下
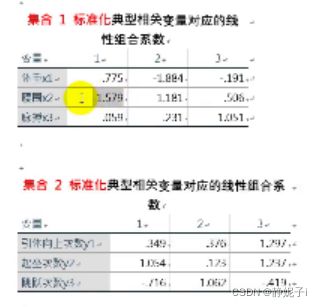
典型相关变量计算:特征值对应的特征向量即为典型相关变量线性组合中的系数
对典型相关系数进行显著性检验
95%的置信水平下:不存在相关性
得到不期望的结果:调整置信水平,继续检验
90%置信水平下,相关性显著
继续第二典型相关系数检验
基于SPSS的操作:
导入变量
分析
相关
典型相关性
导出:相关描述需要修改:
显著的典型相关系数只有第一个(p值小于0.1,置信水平90%,2,3行p值很大认为不存在显著性,可删去不看)
典型相关分析的拓展
从相关矩阵出发计算典型相关
典型载荷分析
典型冗余分析
总结:
典型相关分析关键步骤:
- 假设数据分布有假设:两组数据服从联合正态分布
- 首先要对两组变量的相关性进行检验(构造似然比统计量 ) 。
p值小于0.05(0.1)表示在95%(90%)的置信水平下拒绝原假设,即认为两组变量有关。

3.确定典型相关变量的个数(直接看典型相关系数对应的P值即可)

- 利用标准化后的典型相关变量分析问题
- 进行典型载荷分析
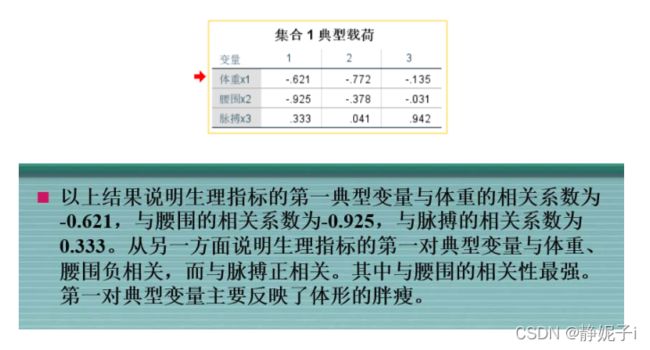
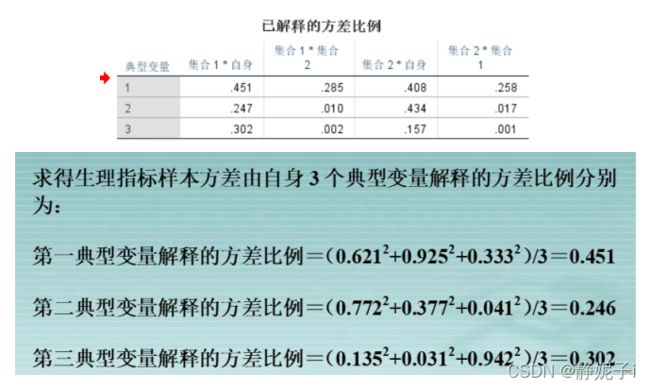
- 计算前 r个典型变量对样本总方差的贡献
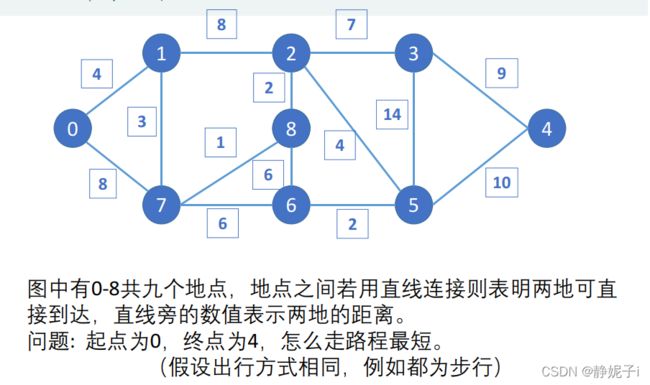
图论最短路
图的基本概念
在线作图:
https://csacademy.com/app/graph_editor/
单源最短路
Dijkstra算法
Bellman-Ford算法
不支持负权回路
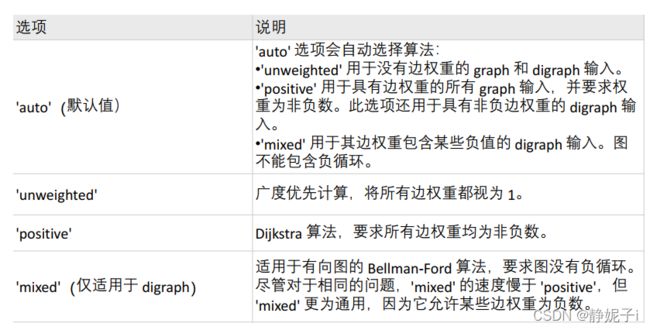
matlab计算最短路径
多源最短路
Floyd算法
是解决任意两点间的最短路径的一种算法,可以正确处理无向图或有向图(可以有负权重,但不可存在负权回路)的最短路径问题。
算法时间复杂度较高O(n3)

 matlab代码:
matlab代码:


还可以编写函数实现:
打印指定两点间最短路径
打印任意两点间最短路径
回归分析
回归分析概念
回归分析的任务就是,通过研究自变量X和因变量Y的相关关系,尝试去解决Y的形成机制,进而达到通过X去预测Y的目的。
(PS:相关性不代表因果性,数据相关不代表其一定存在某种因果关系。绝大多数情况下,我们没有能力去探究严格的因果关系,只好退而求其次,改成通过回归分析,研究相关关系)
(PS:Y即为因变量,在实际应用中,Y常常是我们需要研究那个核心变量)
(PS:X是自变量,也即解释变量)
回归分析分类
回归分析任务
回归分析的使命:
使命1:识别重要变量:识别并判断哪些X变量和Y是真的相关,哪些不是。“变量选择”(逐步回归法,X一个一个带入只留下显著的)
使命2:判断相关性的方向:判断有用的X和变量同Y的相关性的正负
使命3:估计权重(回归系数):确定重要的X变量的前提下,赋予不同的X不同的权重,也就是不同的回归系数,进而确定不同变量之间的相对重要性。
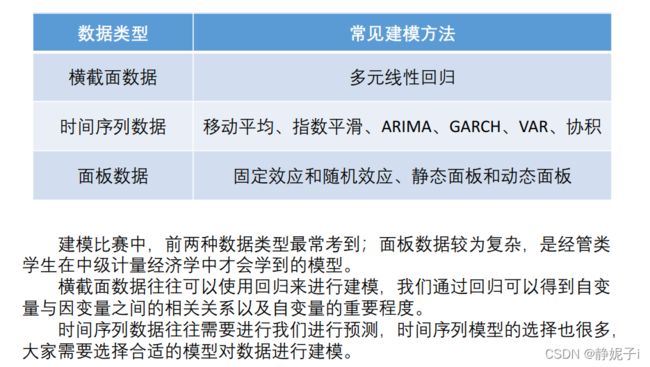
数据的分类
横截面数据:
在某一时点收集的不同对象的数据
例如:
(1)我们自己发放问卷得到的数据
(2)全国各省份2018年GDP的数据
(3)大一新生今年体测的得到的数据
时间序列数据:
对同一对象在不同时间连续观察所取得的数据
例如:
(1)从出生到现在,你的体重的数据(每年生日称一次)。
(2)中国历年来GDP的数据。
(3)在某地方每隔一小时测得的温度数据
面板数据:
横截面数据与时间序列数据综合起来的一种数据资源
例如:
2008‐2018年,我国各省份GDP的数据
数据的收集
多元线性回归分析
一元线性回归
回归系数的解释
内生性的定义和度量
无偏性:描述真实值和估计值的偏差,用期望描述
一致性:n趋于无穷时,估计值能够收敛到真实值
内生性:即误差项与自变量的相关性
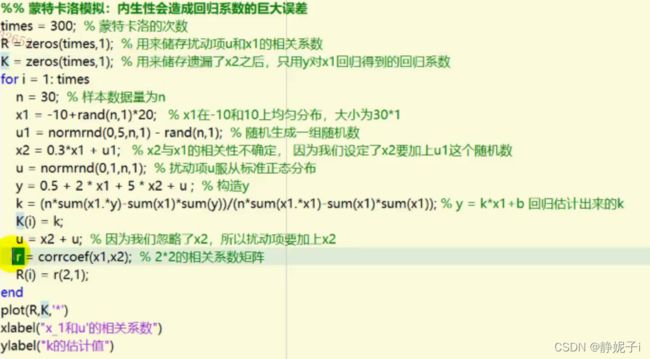
内生性的蒙特卡洛模拟
解决内生性的方法
回归系数的解释
β \beta β 0截距项不考虑其意义
重点解释核心解释变量的系数意义及其显著性
四类模型回归系数的解释
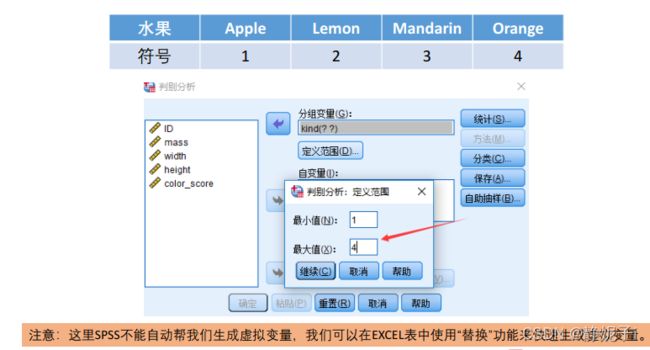
特殊变量的处理:虚拟变量
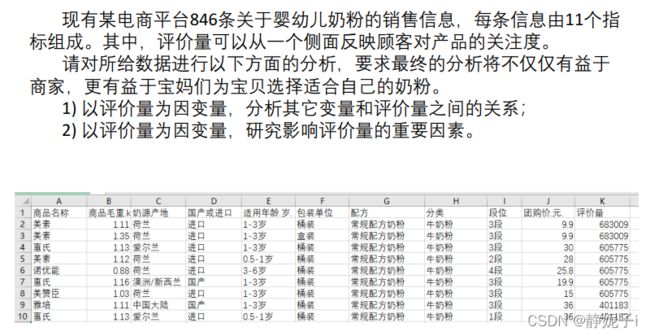
举例进行回归分析
题目描述
使用软件
SPSS和matlab 在虚拟变量的处理比较麻烦
采用Stata
蒙特卡洛模拟
布丰投针实验引入
定义:
 原理:
原理:
由⼤数定理可知,当样本容量⾜够⼤时,事件的发⽣频率即为其概率
应用:
求解有约束的非线性规划问题
规划问题:
目标函数达fx到最大/最小:eg f(x)=2x1+3x2(x1,x2决策变量)(gx不等式约束,hx等式约束)
非线性规划只能求近似解(局部最优解,从初始值x0开始)
蒙特卡洛模拟:枚举并带入以求得初始值x0,再通过各种规划算法求解近似值
01规划问题
用01矩阵表示某本书是否在某店购买的情况
随机数生成矩阵模拟随机购买情况,计算并更新花费最小值
蒙特卡洛模拟n次
导弹追踪问题
根据题意将此追踪抽象成数学问题,通过分隔时间片,将连续问题转化为离散问题,再通过蒙特卡洛模拟追踪过程,一步步逼近最终结果
旅行商问题
当n很大时,用蒙特卡洛模拟会很慢
数学规划模型
概述
线性规划LP
非线性规划NLP:在初始值周围搜索近似解
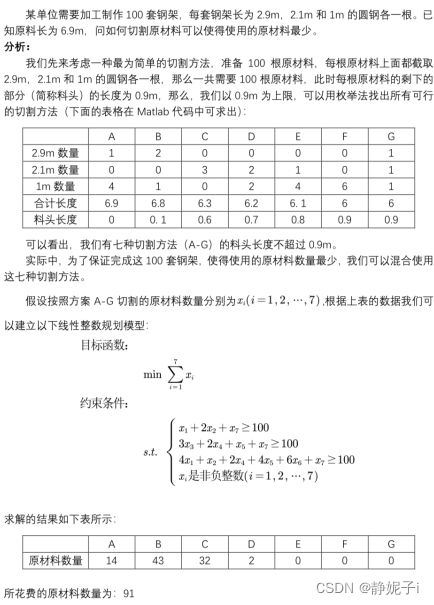
整数规划:
线性规划问题求解
线性规划典型例题
整数规划
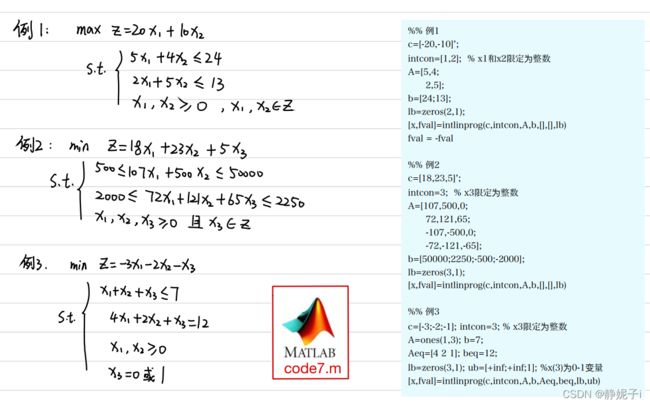
整数规划的典型例题:
非线性规划问题
matlab求解非线性规划
最大最小化模型
多目标规划模型
分类模型
逻辑回归
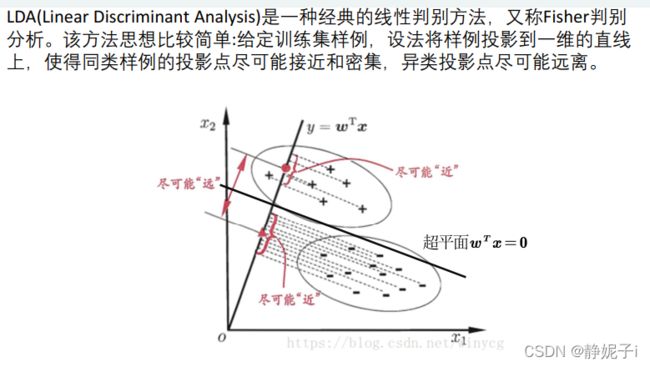
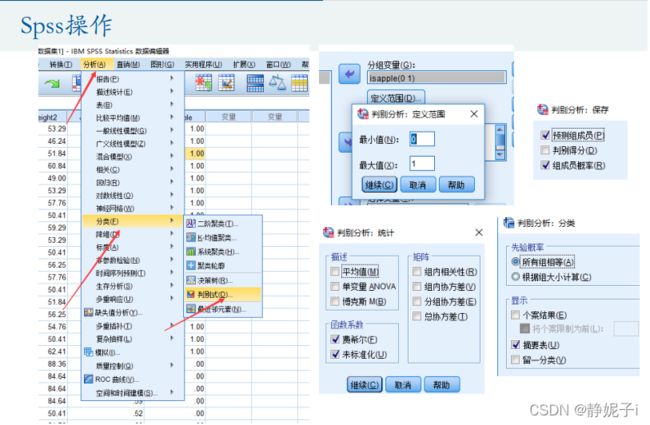
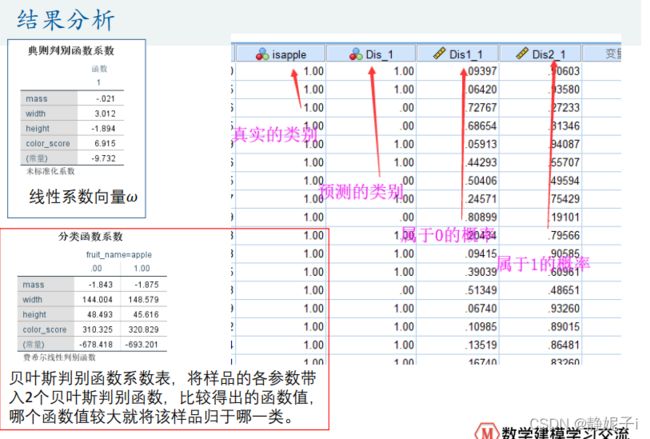
Fisher线性判别分析
多分类问题
聚类问题
K-means聚类算法
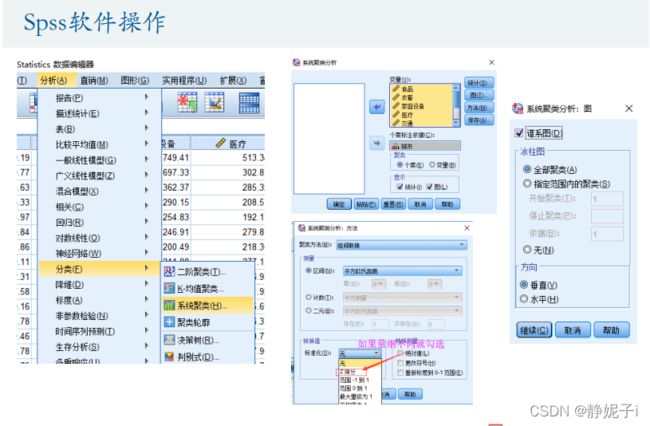
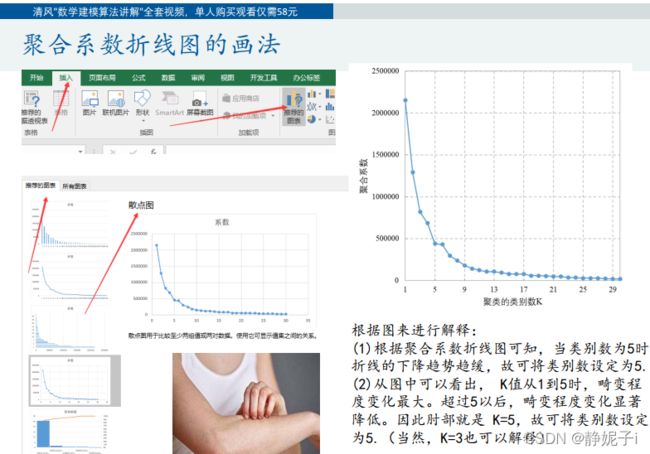
系统(层次)聚类
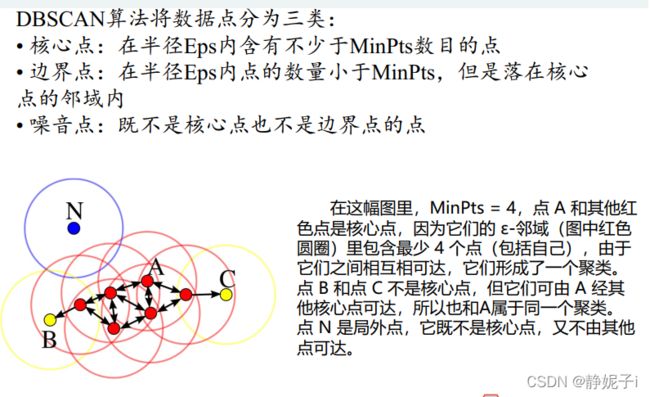
基于密度的聚类算法dbscan算法
时间序列分析

时间序列概念:


时间序列分解:
因为时间序列是某个指标数值长期变化的数值表现,所以时间序列数值变化背后必然蕴含着数值变换的规律性,这些规律就是时间序列分析的切入点。
一般情况下,时间序列的数值变化规律有以下四种:
长期变动趋势
季节变动规律
周期变动规律
不规则变动(随机扰动项)
一个时间序列往往是以上四类变化形式的叠加

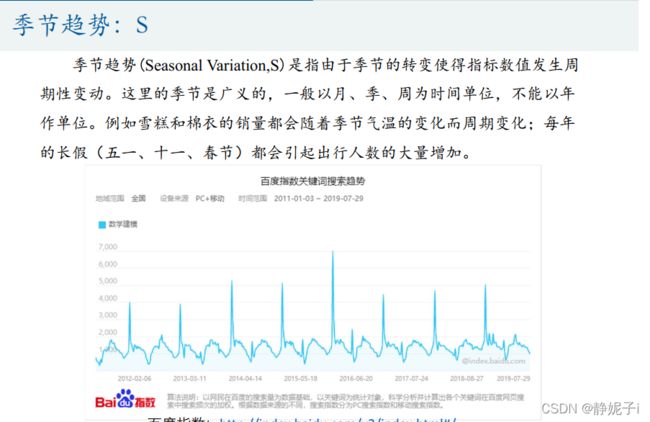 可以使用百度指数搜索
可以使用百度指数搜索

 四种变动与指标数值最终变动的关系可能是叠加关系,也可能是乘积关系。
四种变动与指标数值最终变动的关系可能是叠加关系,也可能是乘积关系。
处理数据:

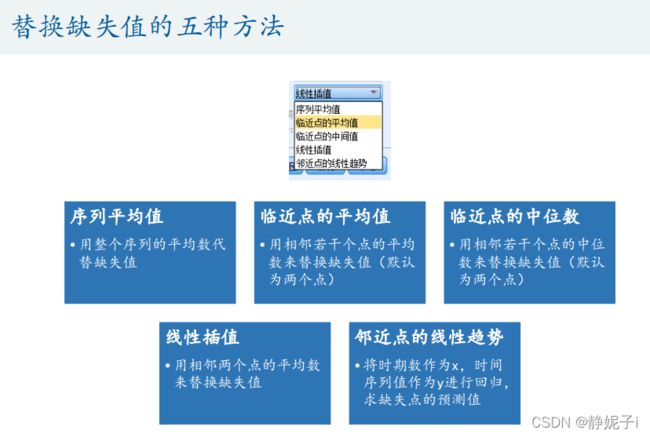
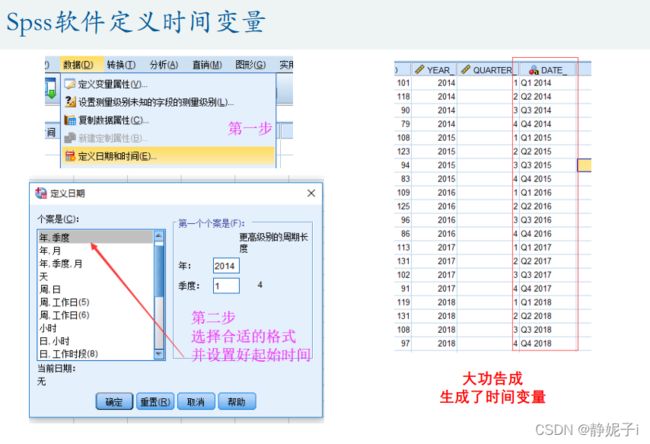 画时间序列图:
画时间序列图:
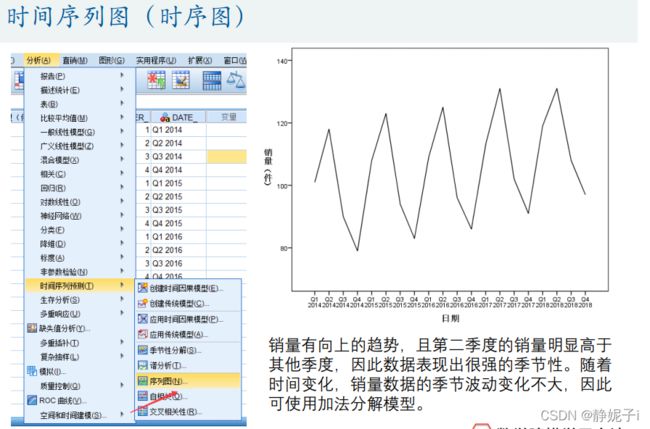
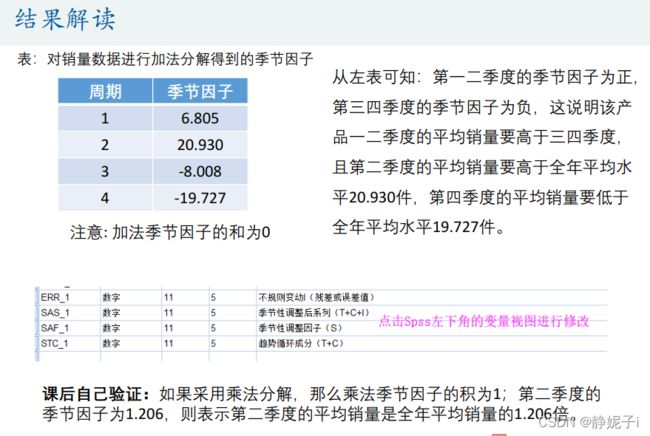
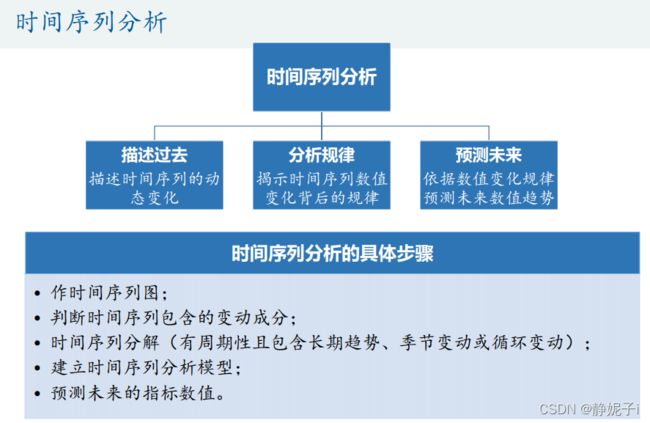 Spss:给定时间序列,自动找到适合的拟合模型
Spss:给定时间序列,自动找到适合的拟合模型
其中提供了指数平滑模型和ARIMA模型