George_Will

机器学习基础：人工智能、机器学习、深度学习的概念和关系（一）

本文属于入门深度学习系列文章的第一篇，该系列专栏主要是记录我在Coursera上学习Andrew Ng的 Machine Learning 和 Deep Learning.AI课程时做的笔记，如果有错误请联系我，我将尽快修改。

1. 人工智能

1.1 概念

让机器能够像人一样思考、行动，替人类完成复杂的工作。

1.2 分类[1]：

弱人工智能： 可以代替人力处理某一领域的工作。
强人工智能： 拥有和人类一样的智能水平，可以代替一般人完成生活中的大部分工作。
超人工智能： 在强人工智能的基础上，像人类一样进行学习，每天自身进行多次升级迭代，而智能水平会完全超越人类。

2. 机器学习

2.1 概念

机器学习是人工智能的一门科学，它是利用数据和以往经验改进算法的研究，是一种能够赋予机器学习的能力以此让它完成直接编程无法完成的功能的方法。但从实践的意义上来说，机器学习是一种通过利用数据，训练出模型，然后使用模型预测的一种方法

2.2 分类

（1）监督学习：

$f(x_i) = y_i\\T=\{(x_1,y_1),(x_2,y_2)···,(x_N,y_N)\}\\$

监督学习是从这样的示例对中学习统计规律，然后对于新的X，给出对应的y。

举个栗子1：

一个学生从波特兰俄勒冈州的研究所收集了一些房价的数据。你把这些数据画出来，看起来是这个样子：横轴表示房子的面积，单位是平方英尺，纵轴表示房价，单位是千美元。那基于这组数据，假如你有一个朋友，他有一套750平方英尺房子，现在他希望把房子卖掉，他想知道这房子能卖多少钱。

我们应用学习算法，可以在这组数据中画一条直线，或者换句话说，拟合一条直线，根据这条线我们可以推测出，这套房子可能卖多少钱。从上图看出来，如果我们用线性函数拟合(红色线)，拟合效果看来不太好，预测值和真实值之间的差距较大；但是，如果我们用二次方程来拟合（蓝色线），预测值和真实值之间的差距就小很多，从预测结果来看，750平方英尺的房子售价预计$200K.

可以看出，监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案”组成。在房价的例子中，我们给了一系列房子的数据，我们给定数据集中每个样本的正确价格，即它们实际的售价然后运用学习算法，算出更多的正确答案。比如你朋友那个新房子的价格。用术语来讲，这叫做回归问题。我们试着推测出一个连续值的结果，即房子的价格。（回归这个词的意思是，我们在试着推测出这一系列连续值属性）

举个栗子2：

假设说你想通过查看病历来推测乳腺癌良性与否

这个数据集中，横轴表示肿瘤的大小，纵轴上，我标出1和0表示是或者不是恶性肿瘤。我们之前见过的肿瘤，如果是恶性则记为1，不是恶性，或者说良性记为0。

我有5个良性肿瘤样本，在标记为1的位置有5个恶性肿瘤样本。现在我们有一个朋友很不幸检查出乳腺肿瘤。假设说她的肿瘤大小为上图红色所指示的大小，那么机器学习的问题就在于，你能否估算出肿瘤是恶性的或是良性的。

用术语来讲，这是一个分类问题，更准确的说是一个二分类问题。

分类指的是，我们试着推测出离散的输出值：0或1良性或恶性，而事实上在分类问题中，输出可能不止两个值。比如说可能有三种乳腺癌，所以你希望预测离散输出0、1、2、3。0 代表良性，1 表示第1类乳腺癌，2表示第2类癌症，3表示第3类，但这也是分类问题，称为多分类问题。

所以，总结一下回归和分类的关系

回归和分类都属于监督学习范畴，数据格式为
回归试着推测出连续的值，而分类试着推出离散的值

举个栗子3：

顺接上一个栗子2，如果我们用于衡量的特征不止一个(肿瘤大小)，还有其它特征，那该怎么办？

以两个特征为例，从一维扩展到二维，同样，我们也是画一条线（称为Decision Boundary，决策边界）在线的左侧为一个分类，在线的右侧为另一个分类。

同样地，我们还可以添加更多特征，延伸到更高维度。

总结一下，监督学习是什么？

监督学习的训练数据样本包含两个部分，其中x表示输入的数据，y表示与x相对于的输出标签，模型要做的就是探索x和y之间的关系，建立两者之间的映射关系（并且要求误差尽可能的小），而这种映射关系具体来说是一个拟合函数，而训练的过程本质上就是寻找合适的函数参数θ的过程。我们训练完模型之后，当我们输入一个新的x，将x作为变量输入模型训练的函数，然后计算出对应的y。进一步，根据y是否是连续值还是离散值，我们又可以细分为回归模型或是分类模型，而分类模型又可以分为二分类和多分类。

常见的监督学习算法：

K-近邻（KNN）
线性回归
逻辑回归
支持向量机
决策树和随机森林
神经网络 （!!）

（2）无监督学习：

上个一节，已经介绍了监督学习。回想当时的数据集，这个数据集中每条数据都已经标明是阴性或阳性，即是良性或恶性肿瘤。所以，对于监督学习里的每条数据，我们已经清楚地知道，训练集对应的正确答案，是良性或恶性了,即已知 (x -> y)

在无监督学习中没有任何的标签，所以我们已知数据集，却不知如何处理，也未告知每个数据点是什么，即训练数据只有没有标签y。

针对这样的数据集，无监督学习的任务就是从一堆数据中学习其内在统计规律或内在结构，可以实现对数据的聚类、降维、可视化、概率估计和关联规则学习。

举个栗子：

① 在数据中心，那里有大型的计算机集群，利用无监督学习可以解决如何让不同的机器协同地工作，从而提高数据中心的工作效率。

② 社交网络的分析，已知你朋友的信息，比如你经常发email的，或是你Facebook的朋友、谷歌+圈子的朋友，我们能否自动地给出朋友的分组呢？即每组（簇）里的人们彼此都熟识。

常见的无监督学习算法：

1）聚类算法

k-平均算法(k-means)
分层聚类算法
最大期望算法(EM)

2）可视化与降维

主成分分析(PCA)
核主成分分析
局部线性嵌入
t-分布随机近临嵌入

3）关联规则学习

Apriori
Eclat

（3）半监督学习：

半监督学习包含大量未标注数据和少量标注数据。主要是利用未标注中的信息，辅助标注数据，进行监督学习。

例如说上传的照片都是大量未标注数据，但会有重复的同一个人的照片，可以通过无监督学习进行分类；如果你为其中一份照片标注了信息，则可以为其他未标注的数据标注信息。

大多数半监督学习算法是无监督式和监督式算法的结合，例如深度信念网络(DBN)。它基于一种互相堆叠的无监督式组件，这个组件叫作受限玻尔兹曼机(RBM)。

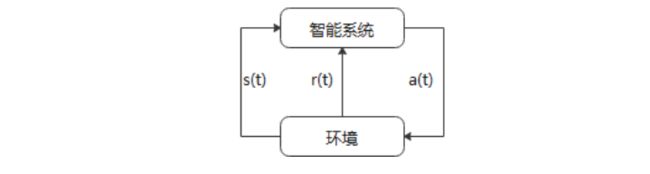
（4）强化学习：

强化学习是指智能系统在与环境的连续交互中学习最佳行为策略的机器学习问题，其本质是学习最优的序贯决策。

强化学习的目标是在所有的策略中选择出价值函数最大的策略，而实际中往往从一个具体的策略出发，不断优化现有策略。

例如，机器人学习行走；AlphaGo学习下棋。

在每一步t，智能系统从环境中观测到一个状态s和一个奖励r，采取一个动作a。环境根据采取的动作决定下一个时刻t+1的状态和奖励。需要学习的策略表示为给定状态下采取的动作，目标不是短期奖励的最大化，而是长期累积奖励的最大化。

（5）主动学习：

主动学习是机器不断给出实例进行人工标注，然后使用标注数据学习预测模型的机器学习问题。主动学习的目标是对学习最有帮助的实例人工标注，以较小的标注代价，达到最好的学习效果。

3. 深度学习

3.1 神经网络[2]、神经元和感知机

([概述，具体内容会在监督学习中介绍](# 5.2 神经元和感知器))

感知机在上世纪50年代末和60年代初由科学家Frank Rosenblatt取得了进展，灵感来自早期又Warren McCulloch与沃尔特·皮兹的神经研究工作。先看下感知机是如何工作的:

感知机的工作原理可以理解为，将输入信号，通过一系列的权值，加权求和以后，通过中间圆形的某个激活函数得出的结果来跟某个阈值进行比较，来决定是否要继续输出。这种工作机制非常的类似我们的大脑的神经元细胞。

如果用向量表示的话，计算过程为：
$1)\quad 偏置\\ W_1:(n_h,n_x) \quad 权重\\ X:(m,n_x) \quad输入数据\\ Z_1=X·W_1^T:（m,n_h)+b\\ A_1=f(Z):（m,n_h)\quad激活函数\\ A1作为下一层的输入，Z_2=A_1·W_2^T\\ ....$

上图为一个三层（不包括输入层）的神经网络：

其中每个小圆圈代表一个感知机模型（或理解为一个神经元）

第 0 层称之为输入层,因为它直接跟输入数据相连；
第 1 和第 2 层称之为隐藏层；
第 3 层为输出层；

第一层网络的各个神经元接收了输入信号，然后通过自身的神经体加权求和以后，输出给下一层神经元。第二层的神经网落的神经单元的输入来自前一层的神经网络的输出。以此类推。最后的经过中间的神经网络的计算以后，将结果输出到输出层。得出最后的结果。这里的输出层我们只让结果输出为一个结果，也可以输出多个结果。一般的分类用途的神经网络，最后会输出跟label相对应个数的输出维度。

3.2 激活函数

所谓激活函数(Activation Function)，就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

在说激活函数之前，我们先要搞明白的一件事，为什么要使用激活函数，不用有什么问题？

在前面的感知机模型中，我们可以看到，神经元对待输入参数是以加权求和的方式来进行运算的。如果我们不使用激活函数，那么我们输出的结果，应该是输入参数的线性叠加的结果，即不论经过多少层网络输出仍然是输入的线性变换。那线性变换也有什么问题呢？

举个例子：

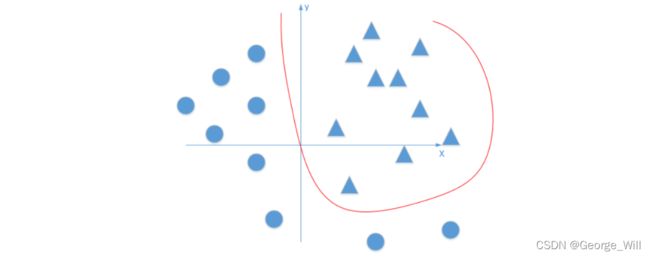
如何用线性函数将三角形和圆形分开？

发现，无论如何划分都无法将三角形和圆形分割开，那怎么办？

如果我们采用非线性的曲线那么就能很好的将三角形和圆形分割开了，因此，回到刚才的问题，激活函数为什么要用非线性的，在一定条件下确实可以采用线性的激活函数，但是在很多情况下我们面临的分类问题常常是无法用线性的分类器分割开来的，因此，我们需要采用非线性的激活函数。

那么，常见的非线性激活函数有哪些呢？

以Sigmoid、tanh以及ReLu为例介绍其优缺点：

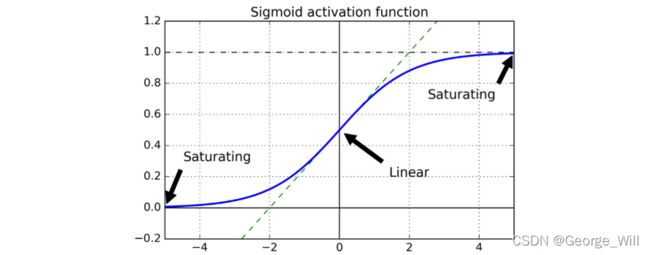
（1）Sigmoid 激活函数

$f(z)=\frac{1}{1+e^{-z}}\\ f(z)'=f(z)(1-f(z))$

优点：

它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1

缺点：

1. 梯度消失

如图所示当f(z)中的z趋向于∞时，曲线趋于平缓，求导之后导数趋于0（现在不理解没关系，后面讲到梯度下降时就能明白了），导致了变量的更新非常慢。

2. 不是以 (0，0) 为中心

3. 运算比较耗时，因为需要用到幂运算

（2）tanh 激活函数

$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\\ tanh(x)'=1-(tanh(x))^2$

与Sigmoid相比：

解决了输出不是0中心的问题，但是梯度消失跟幂运算还是存在

（3）ReLu激活函数