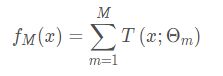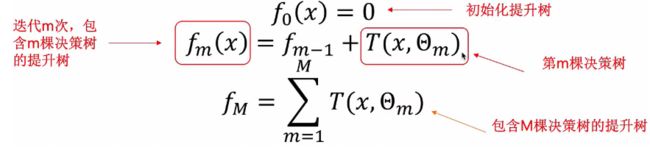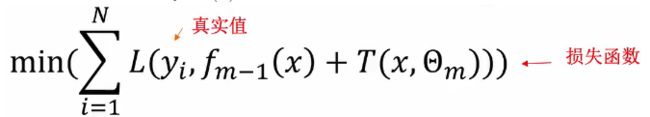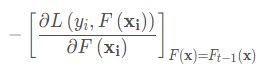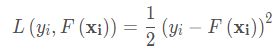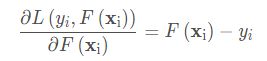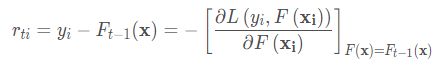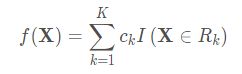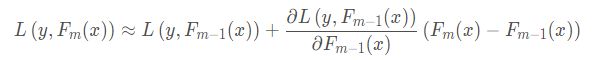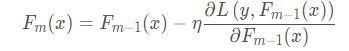推荐系统之GBDT+LR
前言
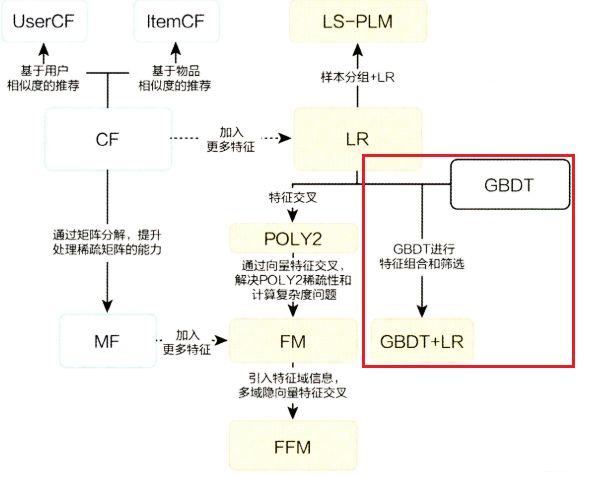
前面讲过的FM与FFM模型虽然增强了模型的交叉能力,但是不管怎样都只能做二阶的交叉,如果想要继续加大特征交叉的维度,那就会出大计算爆炸的情况。所以Facebook提出了梯度提升树(GBDT)+逻辑回归(LR)的模型,具体来说首先利用GBDT自动将特征进行筛选和组合,进而生成新的离散特征向量,然后再把特征向量当作LR模型输入,从而预估CTR。关于逻辑回归(LR)的部分前面已经讲过了,这里具体的讲一下GBDT这个大家伙。在讲解之前先看一章图来了解一下传统推荐模型的进化关系图,讲完这一章传统的推荐算法模型就基本告一段落了,这个图中出现的所有模型都已经一一被讲解过了,大家可以看我主页来进行了解。
一、GBDT模型
GBDT全称梯度提升决策树,在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一,即可以用于分类也可以用于回归还可以筛选特征。这个算法非常重要, 现在机器学习算法最常用的XGBOOST,Lightgbm, catboost这几大巨头算法都是基于这个算法的基础上进行发展起来的。介绍GBDT之前我觉得有必要先介绍一些BDT,这是以CART决策树为基学习器的集成学习方法, 关于集成学习,我还会写文章来进行介绍。
(1)BDT
首先提升树模型可以理解为多个决策数的加法:
其中函数T()代表决策树,M表示树的个数,提升树采用的是向前分布算法,首先确定提升树![]() ,第m步的模型是:
,第m步的模型是:
通过将损失函数极小化来确定下一颗树的参数。在这里总结一下回归算法选择的损失函数一般是均方差或者绝对值误差;而在分类算法中一般的损失函数选择对数函数来表示。
这里借用一下一位大佬的总结:
boosting方法之前已经提到过, 是由多个弱学习器进行组合得到的一个强学习器, 而每个弱学习器之间是相互关联的, AdaBoost是boosting家族的一员, 它与BDT不同, AdaBoost中弱学习器之间的关联关系是前一轮学习器表现不行的样本, 而GDT中弱学习器之间的关联是残差。
给定一些训练样本, 先训练第一个弱学习器, BDT里面的话就是决策树了,这种决策树一般都是CART, 训练完了第一个学习器, 就可以对样本进行一个预测, 此时会得到一个与真实标签的一个残差, 那么就可以用这个残差来训练后面的学习器, 也就是第二个分类器关注于与前面学习器与真实标签的差距, 这样依次类推, 最后会得到n个弱分类器。 那么我这n个分类器进行加和, 就得到了最终的学习器。最后就是用这个东西进行预测。根据上面的这个简单过程, 我们再来理解一下《统计学习方法》里面的公式, 提升树实际上是加法模型和前向分布算法, 表示为:
在前向分布算法的第m mm步时, 给定当前的模型![]() ,求解:
,求解:
这样就可以得到第m棵决策树![]() 。但是要注意的是提升树算法中的基学习器是CART树的回归树。这就是BDT算法的一般流程, 简单总结就是初始化一棵树, 计算残差, 根据残差拟合一棵树, 然后更新。下面就是完整的提升树算法:
。但是要注意的是提升树算法中的基学习器是CART树的回归树。这就是BDT算法的一般流程, 简单总结就是初始化一棵树, 计算残差, 根据残差拟合一棵树, 然后更新。下面就是完整的提升树算法:
介绍完BDT接下来讲解一下GBDT,如果不懂CART如何生成的小伙伴可以参考我这篇文章。
(2)GBDT原理详解
提升树利用加法模型和前向分布算法实现学习的优化过程,但是在损失函数优化的时候往往不是很容易进行,于是这时候就需要大佬来横空出世解决这类问题了,那就是Friedman大神提出利用最速下降的近似方法, 即利用损失函数的负梯度来拟合基学习器。
用这个损失函数的负梯度来作为前面提到的残差的近似值,至于为什么这么做,首先先使用平方均值损失函数来进行解释,首先还是列一下平方损失函数公式:
对![]() 求导得到:
求导得到:
这个时候就会发现这个导数正好是残差的相反数(对y-![]() 求导,需要注意的是前面还有一个负号呢,别忘记了):
求导,需要注意的是前面还有一个负号呢,别忘记了):
当然了这只是一个特例了,那么如何老证明其他函数呢,为什么说是近似呢,为什么上面列的平方残差函数是相等呢?别急,一个伟大的泰勒公式为你搞定!
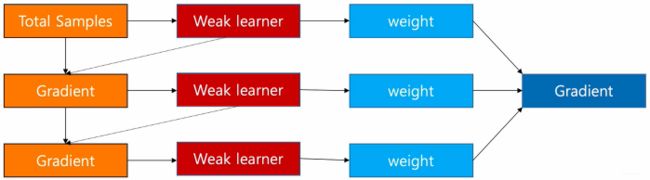
这其实就是GBDT的核心了, 即利用损失函数的负梯度作为回归问题提升树算法中的残差的近似值去拟合一个回归树。gbdt 每轮迭代的时候,都去拟合损失函数在当前模型下的负梯度。这样每轮训练的时候都能够让损失函数尽可能快的减小,尽快的收敛达到局部最优解或者全局最优解。下面就是GBDT的梯度提升流程(这里是宏观的角度, 即分类器是个大类), 和BDT差不多,只不过残差这里直接用负梯度进行了替代。
如图所示:
可以发现GBDT和提升树的区别是残差使用了损失函数的负梯度来替代, 且每个基学习器有了对应的参数权重。gbdt通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单,并且是低方差和高偏差的(因为训练的过程是通过降低偏差来不断提高最终分类器的精度)。 弱分类器一般会选择为CART TREE(也就是分类回归树)。由于上述高偏差和简单的要求每个分类回归树的深度不会很深。最终的总分类器是将每轮训练得到的弱分类器加权求和得到的(也就是加法模型)。这就是GBDT的训练流程了, 当然要明确一点, gbdt无论用于分类还是回归一直都是使用CART回归树, 这个原因后面会说, 既然是用的回归树, 我们就有:
这时候流程图就可以转化为:
算法第 1 步初始化,估计使损失函数极小化的常数值, 它是只有一个根结点的树。第 2(a) 步计算损失函数的负梯度在当前模型的值,将它作为残差的估计。对于平方损失函数,它就是通常所说的残差,对于一般损失函数,它就是残差的近似值。因为对于平方损失函数来说泰勒公式二阶导就为0了,所以可以不用约等于,但是对于其余的损失函数来说不一定。第 2(b) 步估计回归树叶结点区域,以拟合残差的近似值。第 2(c )步利用线性搜索估计叶结点区域的值,使损失函数极小化。第 2(d) 步更新回归树。第 3 步得到输出的最终 模型f^(x)。
(3)从梯度下降的角度考虑GDBT
现在有一个很严肃的问题,也是一个扩展问题了。GBDT叫做梯度提升树, 这和梯度下降有什么关系呢?简单的来说就是一个是在函数空间,一个是在参数空间,而GBDT的求解过程就可以理解为梯度下降在函数空间的优化过程。 首先, 在梯度下降里面,我们是可以通过一阶泰勒展开来证明负梯度方向是目标函数下降最快的方向,现在看图:
上图就是一位大佬总结的梯度下降的参数更新由来,那么对于GBDT呢?首先我们将其损失函数展开:
这里同样根据上面的分析过程,损失函数下降最快的方向同样也是负梯度方向,即
所以在梯度下降和GBDT中,都是梯度下降的原理,只不过在梯度下降中,是参数空间中的优化,每次迭代得到的是参数的增量(负梯度乘上学习率), 而GBDT中,是函数空间中的优化,这个函数会拟合负梯度,在GBDT中,这个函数就是一棵棵决策树。 要得到最终结果,只需要把初始值或者初始的函数加上每次的增量。
二、GBDT+LR
前面讲了很多关于GBDT的东西,小伙伴们如果第一篇看按不太懂,还是建议多看几遍吧,我当时也是反反复复看了好几遍才学会的。关于LR的内容在这里就不多做叙述了,感兴趣的小伙伴可以我关于LR讲解的文章。接下来讲讲这个模型是如何在推荐系统中发挥作用的。
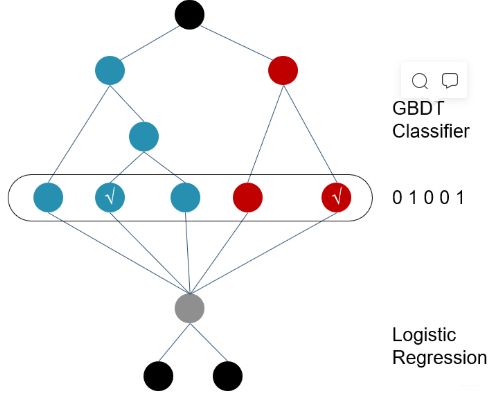
2014年, Facebook提出了一种利用GBDT自动进行特征筛选和组合, 进而生成新的离散特征向量, 再把该特征向量当做LR模型的输入, 来产生最后的预测结果, 这就是著名的GBDT+LR模型了。GBDT+LR 使用最广泛的场景是CTR点击率预估,即预测当给用户推送的广告会不会被用户点击。模型示意图如下所示:
训练时,GBDT 建树的过程相当于自动进行的特征组合和离散化,然后从根结点到叶子节点的这条路径就可以看成是不同特征进行的特征组合,用叶子节点可以唯一的表示这条路径,并作为一个离散特征传入 LR 进行二次训练。比如上图中, 有两棵树,x为一条输入样本,遍历两棵树后,x样本分别落到两颗树的叶子节点上,每个叶子节点对应LR一维特征,那么通过遍历树,就得到了该样本对应的所有LR特征。构造的新特征向量是取值0/1的。 比如左树有三个叶子节点,右树有两个叶子节点,最终的特征即为五维的向量。对于输入x,假设他落在左树第二个节点,编码[0,1,0],落在右树第二个节点则编码[0,1],所以整体的编码为[0,1,0,0,1],这类编码作为特征,输入到线性分类模型(LR or FM)中进行分类。预测时,会先走 GBDT 的每棵树,得到某个叶子节点对应的一个离散特征(即一组特征组合),然后把该特征以 one-hot 形式传入 LR 进行线性加权预测。
需要注意的是树模型不能处理大量高维度离散数据的原因是容易导致过拟合, 但是具体是怎么导致的过拟合呢? 看下图吧。
这个模型也是工业上非常喜欢使用的模型, 下面除了上面这些关键点, 再整理几个工业上使用这个模型的细节:
GBDT+LR模型, GBDT的输入特征一般不能是高维稀疏的id离散特征, 树模型是不喜欢这种特征的。原因就是上面这个了, 所以如果有大量的id类特征, 一定要放到LR这块里面,也就是让连续的特征过gbdt, 然后得到输出的新特征和离散特征走LR。
GBDT+LR模型是可以进行增量训练的, 所谓增量训练,就是定期(比如一个小时)用新的数据对模型进行局部的更新,使的模型更加反映实时性的数据变化, 对于树模型来讲是不能进行增量更新的,因为这种模型没法局部, 训练只能是从头训练(全量更新模式), 而GBDT+LR模型之所以能增量更新,也不是更新GBDT这块,而是LR这块可以进行增量更新。 适合增量更新的模型一般是类似于神经网络这种才可以, 可以冻结某些层,用新数据只更新某些层这种。所以GBDT的更新周期要比LR长。
总结
介绍到这里基本就完事了,但是说归说原理明白的再清楚也只不过是书本上的内容,这些数学公式并不能让你更好的去应用这个模型,只不过是赋予这些模型一些合理的解释罢了,真正需要实际应用的只有代码,后期我也会对这个模型进行训练,到时候再进行补充代码。
注:本博客参考的是翻滚的小强博主,也是我唯一关注的博主,绝对是一个强劲的大佬,大家可以看看他的文章。