Python数据分析实战之葡萄酒质量分析

1. 明确需求和目的

以葡萄酒类型为标签，分为白葡萄酒和红葡萄酒。比较这两种葡萄酒的差别并选取葡萄酒的化学成分：固定酸度、挥发性酸度、柠檬酸、氯化物、游离二氧化硫、总硫度、密度、PH值、硫酸盐、酒精度数共11个，针对酒的各类化学成分建立线性回归模型，从而预测该葡萄酒的质量评分。

2. 数据收集

• 数据集为“winequality-both.csv",共有6497条数据，共13个特征.
• 数据链接：https://pan.baidu.com/s/1dXeIT20OWgtGvJgSZEqRFQ
  提取码：0g7m

3. 数据预处理

3.1 数据整合

3.1.1 加载相关库和数据集

• 使用的库有：pandas、numpy、matplotlib、seaborn、statsmodels
• 使用的数据集：winequality-both.csv
  
  

3.1.2 数据概览

从上图可以看出特征和质量评分的均值和方差，分位数等，其中，质量评分的均值为5.818378。

3.2 数据清洗

3.2.1 列名重命名

从上面发现列名不符合Python的命名规范，对列名进行一下重命名，采用下划线命名法：

3.2.2 数据类型处理

查看各个列的数据类型：

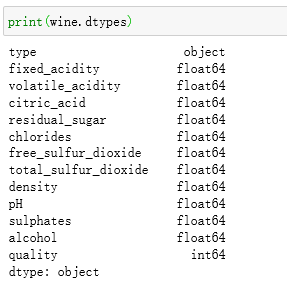
从上图可以看出，除了葡萄酒的type位object类型，其余特征的数据类型都为float型，没有问题，所以不需要进行数据类型处理。

3.2.3 缺失值处理

查看缺失值情况：

发现没有缺失值，所以不需要进行缺失值处理。

3.2.4 异常值处理

简单查看一下是否有异常值：

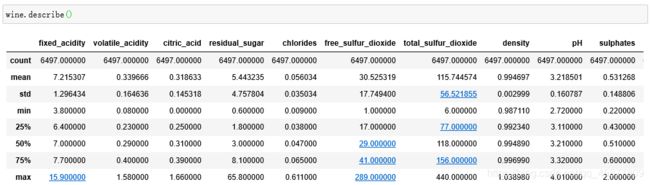
没发现明显的异常值，不需要进行处理。

4. 数据分析

4.1 质量评分分析

4.1.1 质量评分的频数统计

可以看出质量评分为3-9分，其中质量评分为6的数量是最多的，其次是评分为5， 质量评分为9的数量是最少的。

4.1.2 质量评分的描述性统计

按葡萄酒的类型分组，分为两组,：红葡萄酒和白葡萄酒。分别打印出两组葡萄酒的质量的摘要统计量。

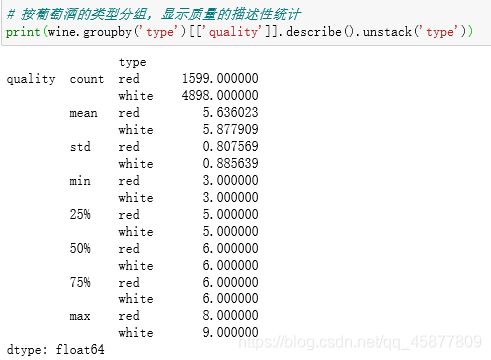
可以看出红葡萄酒和白葡萄酒的数据量相差很大，但均值、最值等都相差不大。

4.1.3 绘制质量评分的直方图

上图显示了不同类型葡萄酒的质量评分密度条形图，可以发现葡萄酒的质量评分大部分集中在5-7分，评分为9的几乎没有。从对比来看，白葡萄酒的质量评分普遍高于红葡萄的质量评分，尤其是评分为6分和7分的较为显著，白葡萄酒评分为6分和7分的数量将近是红葡萄酒的2倍。不过，评分为5的白葡萄酒和红葡萄酒的数量相当，甚至，红葡萄酒更胜一筹。

4.1.4 T检验

对不同葡萄酒的质量评级进行t检验（原假设设为红白两种葡萄酒质量相同）

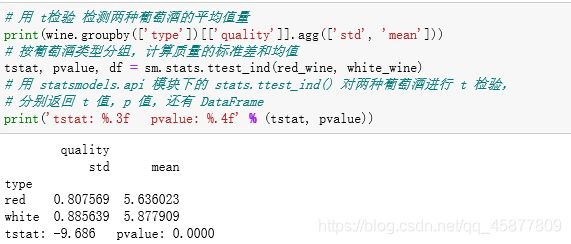
从检验的结果来看，p值<0.05，拒绝原假设，即认为红白两种葡萄酒质量有显著性差异，并且从均值上来看白葡萄酒的平均质量等级在统计意义上大于红葡萄酒的平均质量等级。

4.2 化学成分间的相关性分析

从各变量的相关系数来看酒精含量、硫酸酯、pH 值、游离二氧化硫和柠檬酸这些指标与质量呈现正相关，即当这些指标的含量增加时，葡萄酒的质量会提高；非挥发性酸、挥发性酸、残余糖分、氯化物、总二氧化硫和密度这些指标与质量呈负相关即当这些指标的含量增加时，葡萄酒的质量会降低。从相关系数可以看出，对葡萄酒质量影响最大的是葡萄酒是酒精含量，其相关系数为0.444，其次是酒的密度，但酒的密度对酒的质量是负影响的。

4.3 建立线性回归模型

4.3.1 选取样本

因为红葡萄酒和白葡萄酒的数据量相差很大，所以各选取200个样本。

4.3.2 自变量标准化

4.3.3 建立回归模型

线性回归模型为：quality= 0.0877fixed acidity -0.2186volatile acidity -0.0159citric_acid+ 0.2072residual_sugar-0.0169chlorides+ 0.1060free_sulfur_dioxide -0.1648density-0.1402total_sulfur_dioxide+0.0706pH+0.1143sulphates+ 0.3185*alcohol+5.8184

4.4 预测

有了线性回归模型，当给出了葡萄酒的化学成分的数据就可以预测该葡萄酒的质量评分。

参考文章：https://blog.csdn.net/weixin_42384784/article/details/106179705