智能算法——遗传算法

概述

遗传算法是一种仿生全局优化算法，模仿生物的遗传进化原理，通过选择、交叉与变异等操作机制，使种群中个体的适应性不断提高，其核心思想是物竞天择，适者生存。

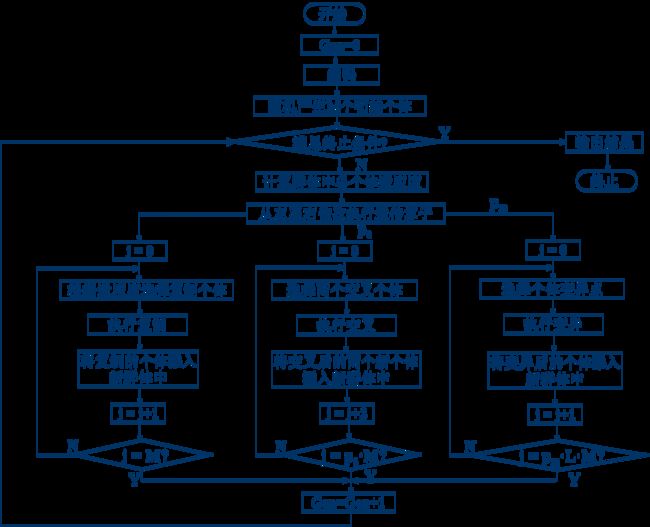
遗传算法示意图

遗传算法相关概念

个体：大多数情况都是由0、1组成的一串字符，代表染色体，也就是变量

种群：多个个体组成的一个集合

适应度：在算法中指计算所得的结果

编码：将一个待求解的问题的实际可行解从其解空间转换到遗传算法所能处理的搜索空间的过程

解码：将遗传算法所搜索到的最优个体的染色体转化成待求解问题的实际最优解的过程

选择操作：根据各个个体的适应度，按照一定的规则，从第带群体中选择出一些优良的个体遗传到下一代群体中

交叉操作：将群体内的各个个体随机搭配成对，对每一个个体，以某个概率遵循某一种规则交换他们之间的部分染色体

变异操作：对群体中的每一个个体，以某一概率改变某个一基因或某一些基因座上的基因值为其他的等位基因

标准遗传算法步骤

1、选择编码策略，把参数集合转换染色体结果空间

2、定义适应度函数，便于计算适应值

3、确定遗传策略，包括选择群体大小，选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数

4、随机产生初始化群体

5、计算群体中的个体或染色体解码后的适应值

6、按照遗传策略，运用选择、交叉和变异算子作用于群体，形成下一代群体

7、判断群体性能是否满足某一指标，或者已经完成预定的迭代次数，不满足则返回第五步，或者修改遗传策略再返回第六步

 各类操作的具体实现

编码：在遗传算法中，多采用二进制编码。举个例子，变量的定义域为,要求精度为，则需要将分成至少个等长的小区域，而每个小区域用一个二进制数表示，于是就有了，即，向上取整可得到，即在这个问题中染色体的长度为19位的二进数

解码：同编码类似

选择操作：在算法中，被选择的个体即为优质个体，会被保留到下一代，而未被选择的个体则会被淘汰，选择操作一般情况下采用轮盘赌选择法。设为一代群体的适应度总和，为这一代群体中第个个体的适应度，那么这个个体被选择的概率为：

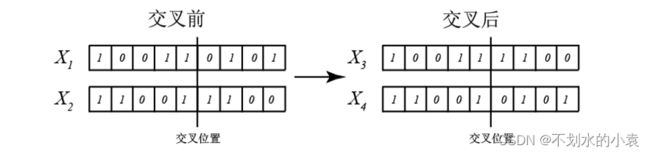
交叉操作：对于二进制编码，常用的交叉方法有单点交叉、多点交叉和均匀交叉等。这里列举一个单点交叉的例子 

变异操作：一般采取二进制变异，如图所示

 代码实现

 求函数在定义域上的最大值

主程序

%主程序
tic;
clear all
clc

popsize = 50;%群体大小
chromlength = 10;%染色体长度
pc = 0.6;%交叉概率
pm = 0.001;%变异概率

pop = initpop(popsize, chromlength);%初始化群体
for i = 1:200%迭代次数
    fitvalue = calobjvalue(pop);%计算目标函数
    [bestindividual, bestfit] = best(pop, fitvalue);%求出群体中适应值最大的个体及其适应度
    y(i) = bestfit;%记录每一代最好的适应值
    n(i) = i;%记录每一代最好的个体
    x(i) = decodebinary(bestindividual) * 10 / 1023;%将最优个体所表示的二进制数映射到可行域上
    newpop = selection(pop, fitvalue);%选择复制
    newpop = crossover(newpop, pc);%交叉
    newpop = mutation(newpop, pm);%变异
    pop = newpop;
end

fplot(@(x)10.*sin(5.*x)+7.*cos(4.*x), [0 10])
hold on
plot(x,y,'r*')
hold off

[y, index] = max(y)%计算最大值及其位置
x = x(index)%计算最大值对应的x值
toc

初始化种群

%初始化
%popsize表示群体大小，chromlength表示染色体长度
function pop = initpop(popsize, chromlength)
pop = round(rand(popsize, chromlength));

将二进制数转化为十进制数

%解码
%将二进制数转化为十进制数
function pop2 = decodebinary(pop)
[px, py] = size(pop);%求种群的行数和列数
for i = 1:py
    pop1(:,i) = 2.^(py-i).*pop(:,i);%二进制转十进制
end
pop2 = sum(pop1,2);%求和

目标函数（适应度）计算

%适应度计算
function objvalue = calobjvalue(pop)
temp1 = decodebinary(pop);%二进制数转十进制数
x = temp1*10/1023;%将二值域映射到变量域
objvalue = 10*sin(5*x)+7*cos(4*x);%计算目标函数值

选择复制

%选择复制
function newpop = selection(pop, fitvalue)
totalfit = sum(fitvalue);%求适应值之和
fitvalue = fitvalue/totalfit;%个体被选择的概率
fitvalue =cumsum(fitvalue);%累加操作
[px, py] = size(pop);
newpop = ones(size(pop));
ms = sort(rand(px,1));
newin = 1;
while newin <= px
    for fitin = 1:px
       if  ms(newin) < fitvalue(fitin)
           newpop(newin,:) = pop(fitin,:);
       end
    end
    newin = newin + 1;
end

交叉

%交叉
%pc为交叉概率，cpoint为交叉位点
function newpop = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
    if (rand < pc)
        cpoint = round(rand*py);
        if cpoint == 0
            cpoint = 1;
        end
        newpop(i,:) = [pop(i,1:cpoint), pop(i+1,cpoint+1:py)];
        newpop(i+1,:) = [pop(i+1,1:cpoint), pop(i,cpoint+1:py)];
    else
        newpop(i,:) = pop(i);
        newpop(i+1,:) = pop(i+1);
    end
end

变异

%变异
%pm为变异概率，mpoint为变异位点
function newpop = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
    if rand < pm
        mpoint = round(rand*py);
        if mpoint == 0
            mpoint = 1;
        end
        newpop(i) = pop(i);
        if any(newpop(i, mpoint))  %判断变异位点是否为0
            newpop(i, mpoint) = 0;
        else
            newpop(i, mpoint) = 1;
        end
    else
        newpop(i) = pop(i);
    end
end

找出群体中最优个体及其最大适应值

%找出群体中最大的适应值及其个体
%bestindividual代表最优的个体
%bestfit代表最大适应值
function [bestindividual, bestfit] = best(pop, fitvalue)
[px, py] = size(pop);
bestindividual = pop(1,:);
bestfit = fitvalue(1);
for i = 2:px
    if fitvalue(i) > bestfit
        bestindividual = pop(i,:);
        bestfit = fitvalue(i);
    end
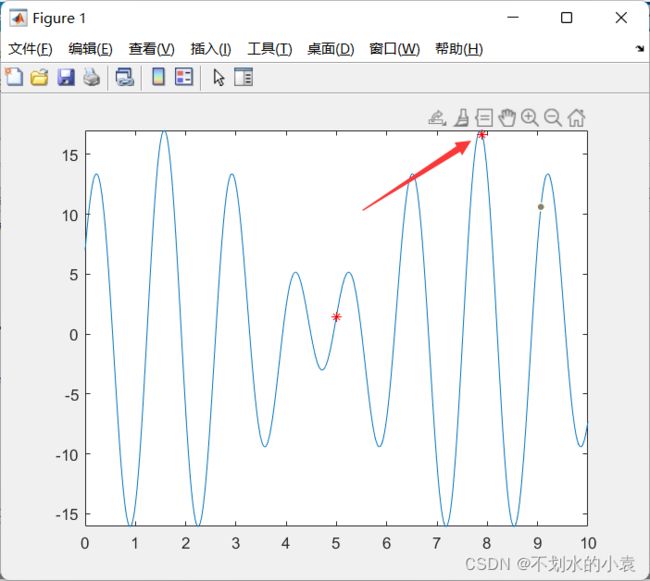
end

得到最后结果：

 结果很明显，200次迭代的结果基本落在2个点上，最优值一眼就能看出来，效果还是非常不错的。

算法优缺点

优点：

1、良好的并行性（操作对象是一组可行解；搜索轨道有多条）

2、强大的通用性（只需利用目标的取值信息，无需梯度等高价值信息）

3、良好的全局优化性和鲁棒性

3、良好的可操作性

缺点：

2、未成熟收敛问题

2、收敛速度较慢，算法实时性欠佳

希望以上内容对你有所帮助，感谢观看！