【数据结构】二叉树算法原理详解+代码+面试题

一、二叉树基本概念

1、二叉树的概念

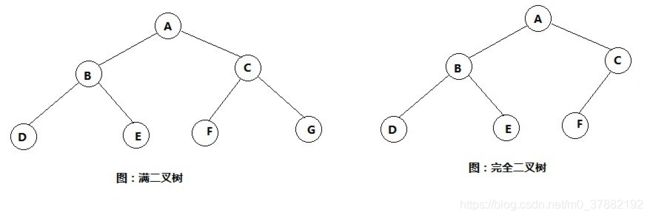
二叉树（Binary Tree）是包含n个节点的有限集合，该集合或者为空集（此时，二叉树称为空树），或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
1）有且仅有一个特定的称为根Root的结点。
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集，其中每个集合本身又是一个棵树，并称为根的子树。

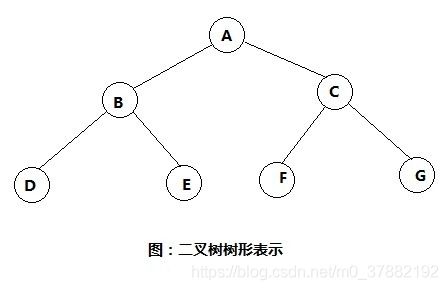
还有一些其他的概念：
1、跟节点：树的顶端节点
2、分支节点：至少有一个子节点的节点
3、度：节点所拥有的子树个数
4、边：一个节点到另一个节点之间的连接
5、路径：连接节点和其后代的节点之间的节点和边的序列
6、节点的层数：从根结点到该节点的所有节点个数
7、 节点的深度：从根节点到该节点边的个数
8、节点的高度：节点的高度是该节点和某个叶子之间存在的最长路径上的边的个数。
9、树的高度：根节点的高度

2、二叉树性质：

（1）在二叉树中，第 i层上至多有$2^{i-1}$个节点（i≥1）
（2）深度为k的二叉树至多有$2^k$−1个节点（k≥1）
（3）对一棵二叉树，如果叶子节点的个数为n₀，度为2的节点个数为n₂，则n₀=n₂+1
（4）具有n个节点的完全二叉树的深度为⌊log₂n⌋+1

3、二叉树的两种存储结构

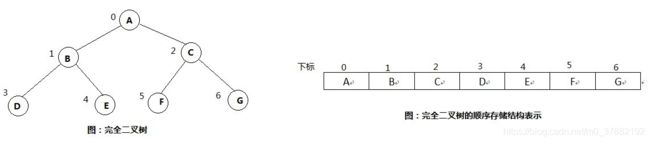
1. 顺序存储

对于完全二叉树而言，可以使用顺序存储结构。但是对于一般的二叉树来说，使用存储结构会有两个缺点，一，如果不是完全二叉树，则必须将其转化为完全二叉树，二是增加了很多虚节点，浪费资源空间。

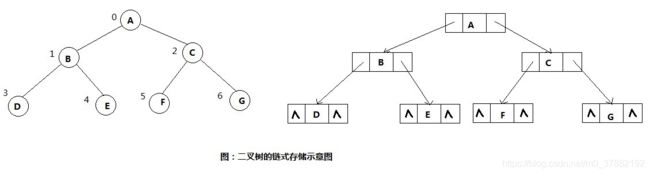
2. 链式存储

这是最常用的一种二叉树存储结构。每个结点设置三个域，即值域，左指针域和右指针域，用data表示值域，lchild和rchild分别表示指向左右子树的指针域。如图所示。

4、二叉树的遍历

在二叉树的操作中，二叉树的遍历是基本的操作，对于二叉树的遍历操作，主要分为：
前序遍历、中序遍历、后序遍历、层次遍历
实际上二叉树的遍历是一个递归的过程
前序遍历的递推公式：
preOrder® = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式：
inOrder® = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式：
postOrder® = postOrder(r->left)->postOrder(r->right)->print r

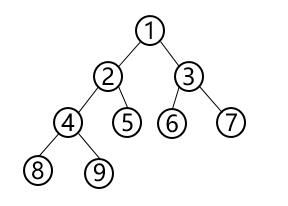
1、前序遍历：根左右
思路：先访问根，然后遍历左子树，再遍历右子树
ABDHIEJCFKG

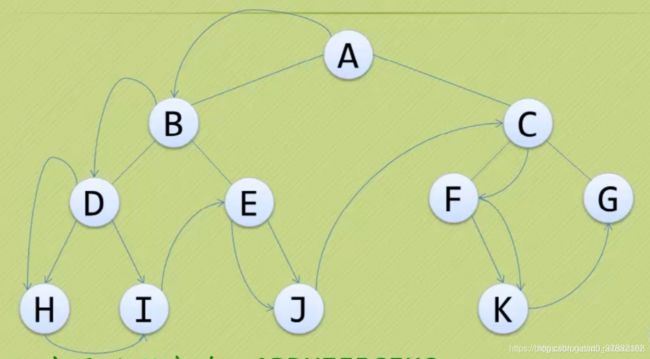
2、中序遍历：左根右
思路：先遍历左子树，再访问根，最后遍历右子树
HDIBEJAFKCG

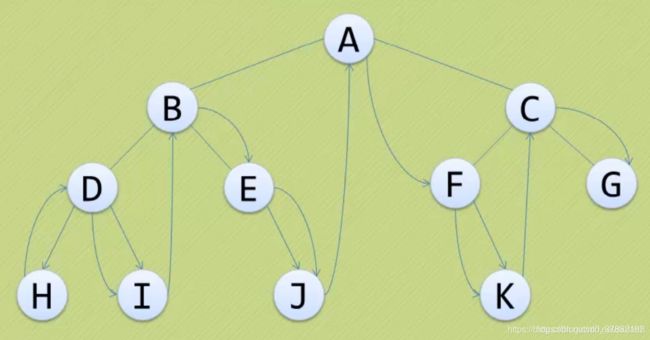
3、后序遍历：左右根
思路：先遍历左子树，再遍历右子树，最后访问根
HIDJEBKFGCA

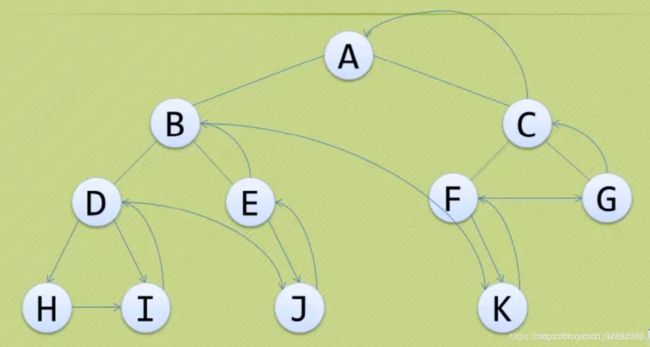
4、层次遍历
思路：从上到小，从左到右遍历
ABCDEFGHIJK

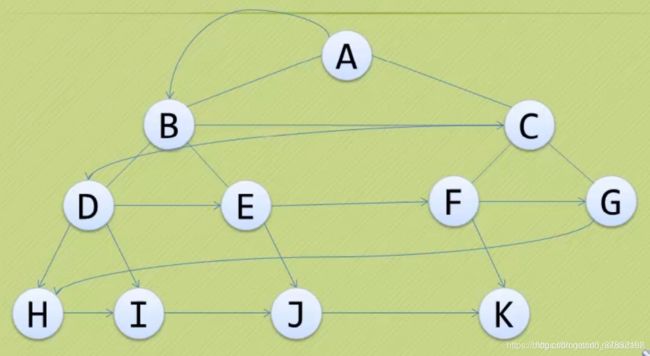
二、二叉树代码举例

二叉树实现代码

# 二叉树的实现
# coding=utf-8

class TreeNode:
	'''二叉搜索树节点的定义'''
	def __init__(self, val):
		self.val = val
		self.left = None
		self.right = None

class OperationTree:
	'''二叉树操作'''
	def create(self, List):
		'''二叉搜索树插入操作'''
		root = TreeNode(List[0])
		lens = len(List)
		if lens >= 2:
			root.left = self.create(List[1])
		if lens >= 3:
			root.right = self.create(List[2])
		return root

	def query(self, root, data):
		'''二叉树查找操作'''
		if root == None:
			return False
		if root.val == data:
			return True
		elif root.left:
			return self.query(root.left, data)
		elif root.right:
			return self.query(root.right, data)

	def PreOrder(self, root):
		'''
		打印二叉树(前序遍历)
		思想：先访问根节点，再先序遍历左子树，然后再先序遍历右子树。总的来说是根—左—右
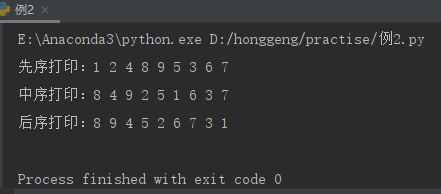
  		上图先序遍历结果为为：1,2,4,8,9,5,3,6,7
		'''
		if root == None:
			return
		print(root.val, end=' ')
		self.PreOrder(root.left)
		self.PreOrder(root.right)

	def InOrder(self, root):
		'''
		中序打印
		思想：先中序访问左子树，然后访问根，最后中序访问右子树。总的来说是左—根—右
  		上图中序遍历结果为为：8,4,9,2,5,1,6,3,7
		'''
		if root == None:
			return
		self.InOrder(root.left)
		print(root.val, end=' ')
		self.InOrder(root.right)

	def BacOrder(self, root):
		'''
		后序打印
		思想：先后序访问左子树，然后后序访问右子树，最后访问根。总的来说是左—右—根
  		上图后序遍历结果为为：8,9,4,5,2,6,7,3,1
		'''
		if root == None:
			return
		self.BacOrder(root.left)
		self.BacOrder(root.right)
		print(root.val, end=' ')

	def BFS(self, root):
		'''
		广度优先
		思想：利用队列，依次将根，左子树，右子树存入队列，按照队列的先进先出规则来实现层次遍历。
  		上图后序遍历结果为为：1,2,3,4,5,6,7,8,9
		'''
		if root == None:
			return
		# queue队列，保存节点
		queue = []
		# res保存节点值，作为结果
		#vals = []
		queue.append(root)

		while queue:
			# 拿出队首节点
			currentNode = queue.pop(0)
			#vals.append(currentNode.val)
			print(currentNode.val, end=' ')
			if currentNode.left:
				queue.append(currentNode.left)
			if currentNode.right:
				queue.append(currentNode.right)
		#return vals

	def DFS(self, root):
		'''
		深度优先
		思想：利用栈，先将根入栈，再将根出栈，并将根的右子树，左子树存入栈，按照栈的先进后出规则来实现深度优先遍历。
  		上图后序遍历结果为为：1,2,4,8,9,5,3,6,7
		'''
		if root == None:
			return
		# 栈用来保存未访问节点
		stack = []
		# vals保存节点值，作为结果
		#vals = []
		stack.append(root)

		while stack:
			# 拿出栈顶节点
			currentNode = stack.pop()
			#vals.append(currentNode.val)
			print(currentNode.val, end=' ')
			if currentNode.right:
				stack.append(currentNode.right)
			if currentNode.left:
				stack.append(currentNode.left)
		#return vals

if __name__ == '__main__':
	List1 = [1,[2,[4,[8],[9]],[5]],[3,[6],[7]]]
	op = OperationTree()
	tree1 = op.create(List1)
	print('先序打印：',end = '')
	op.PreOrder(tree1)
	print("")
	print('中序打印：',end = '')
	op.InOrder(tree1)
	print("")
	print('后序打印：',end = '')
	op.BacOrder(tree1)
	print("")
	# print('BFS打印 ：',end = '')
	# bfs = op.BFS(tree1)
	# print("")
	# print('DFS打印 ：',end = '')
	# dfs = op.DFS(tree1)
	# print("")

结果

三、二叉树面试题

1、求二叉树中的节点个数

// An highlighted block

2、求二叉树的深度（高度）

'''
104. 二叉树的最大深度
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：给定二叉树 [3,9,20,null,null,15,7]，
'''
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def create(self, List):
        '''二叉搜索树插入操作'''
        root = TreeNode(List[0])
        lens = len(List)
        if lens >= 2:
            root.left = self.create(List[1])
        if lens >= 3:
            root.right = self.create(List[2])
        return root

    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        left = self.maxDepth(root.left)
        right = self.maxDepth(root.right)
        return max(left,right) + 1

if __name__ == '__main__':
    List1 = [1,[2,[4,[8],[9]],[5]],[3,[6],[7]]]
    List2 = [3,[9,[None],[None]],[20,[15],[7]]]
    op = Solution()
    tree = op.create(List2)
    t = op.maxDepth(tree)
    print(t)

3、求二叉树中叶子节点的个数

// An highlighted block

4、已知一棵二叉树前序遍历和中序遍历分别为ABDEGCFH和DBGEACHF，则该二叉树的后序遍历为?

已知一棵二叉树bai前序遍和中序遍历分du别为ABDEGCFH和DBGEACHF，则该二叉树的zhi后序遍历dao是DGEBHFCA。

前序遍历的第一个节点为根节点，由前序遍历可知，A为根节点。中序遍历的根节点前面的节点均为左子树的节点，所以左子树上的节点为DBGE。去掉根节点和左子树节点，右子数节点为CHF。前序遍历的第二个节点为B，由2知B为左子树节点，所以B为左子树的根节点。

由前序遍历，DEG在B节点下面，由中序遍历，D是B的左节点，GE是B的右节点。由前序遍历，E是G的根节点，由中序遍历，G是E的左子节点。由前序遍历，C是二叉树的右根节点，由中序遍历，C不含左子节点，HF为C的右子节点。由前序遍历，F为H的根节点，由中序遍历，H为F的左子节点。

在二叉树中，求后序遍历，先左后右再根，即首先遍历左子树，然后遍历右子树，最后访问根结点。则该二叉树的后序遍历是DGEBHFCA。

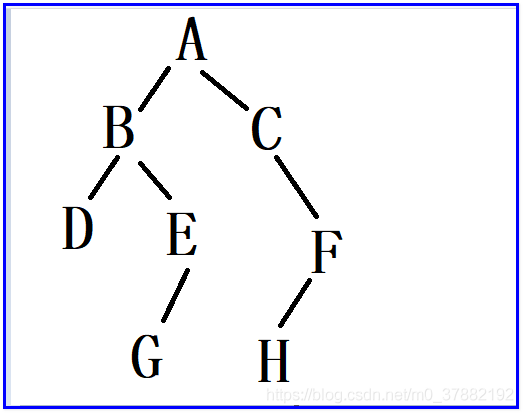
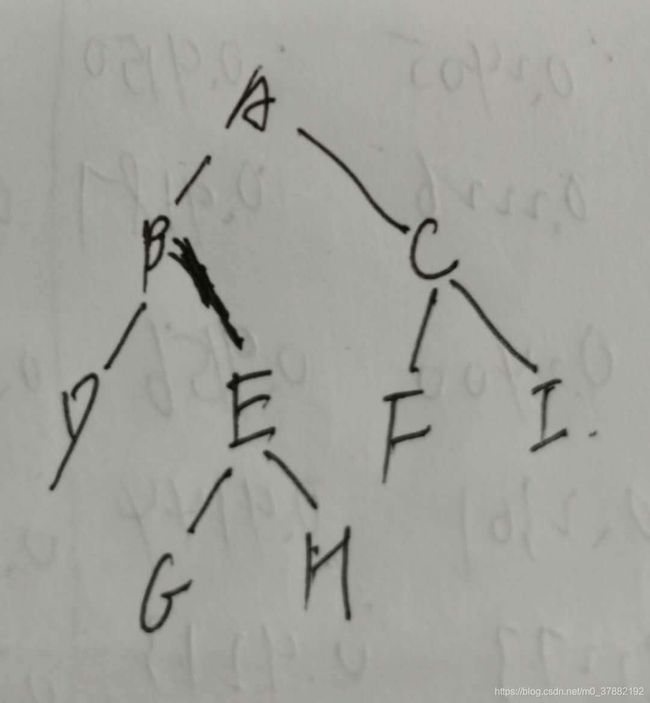
5、已知一棵二叉树，前序遍历的节点顺序是：ABDEGHCFI，中序遍历的节点顺序是：DBGEHAFCI，其后序遍历的顺序是？

已知一棵二叉树，前序遍历的节点顺序是：ABDEGHCFI，中序遍历的节点顺序是：DBGEHAFCI，其后序遍历的顺序是：DGHEBFICA

四、leetcode-二叉树刷题

101. 对称二叉树

给定一个二叉树，检查它是否是镜像对称的。
例如，二叉树[1, 2, 2, 3, 4, 4, 3]是对称的。
但是下面这个[1, 2, 2, null, 3, null, 3]则不是镜像对称的:

# 递归算法
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:# 如果根为空，则返回ture
            return True
        def dfs(left,right):
            if not (left or right):# 如果left和right都为空，则返回ture
                return True
            if not (left and right):# 如果如果left和right有一个不为空，则返回False
                return False
            if left.val != right.val:# 如果如果left和right不相等，则返回False
                return False
            return dfs(left.left,right.right) and dfs(left.right,right.left)
        return dfs(root.left,root.right)# 用递归函数，比较左节点，右节点

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：给定二叉树 [3,9,20,null,null,15,7]，

# def PreOrder(self, root):
#     '''打印二叉树(前序遍历)根—左—右'''
#     if root == None:
#         return
#     print(root.val, end=' ')
#     self.PreOrder(root.left)
#     self.PreOrder(root.right)
#
# List1 = [1,[2,[4,[8],[9]],[5]],[3,[6],[7]]]
# op = PreOrder(List1)

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def create(self, List):
        '''二叉搜索树插入操作'''
        root = TreeNode(List[0])
        lens = len(List)
        if lens >= 2:
            root.left = self.create(List[1])
        if lens >= 3:
            root.right = self.create(List[2])
        return root

    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        left = self.maxDepth(root.left)
        right = self.maxDepth(root.right)
        return max(left,right) + 1

if __name__ == '__main__':
    List1 = [1,[2,[4,[8],[9]],[5]],[3,[6],[7]]]
    List2 = [3,[9,[None],[None]],[20,[15],[7]]]
    op = Solution()
    tree = op.create(List2)
    t = op.maxDepth(tree)
    print(t)

226. 翻转二叉树

翻转一棵二叉树
输入:[4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
预期结果:[4,7,2,9,6,3,1]

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution(object):
    def invertTree(self, root):
        # 递归终止条件判断，为空时则返回
        if not root:
            return root
        # 使用递归交换当前结点的左子树和右子树
        left = self.invertTree(root.left)
        right = self.invertTree(root.right)
        # 当前节点的左右子树交换
        root.right,root.left = left,right
        # 函数返回时就表示当前这个节点，以及它的左右子树
        # 都已经交换完了
        return root

543. 二叉树的直径

617. 合并二叉树