哈夫曼树与哈夫曼编码及代码实现
目录结构
-
- 数据压缩
- 哈夫曼编码
- 哈夫曼树
- 代码演示
数据压缩
含义
通过对数据重新的编码,减少数据占用的空间存储;使用的时候再进行解压缩,恢复数据的原有特性。
类别
- 无损压缩——压缩过程没有数据丢失,解压得到原有数据特性。
- 有损压缩——压缩过程会丢失数据的部分信息,如压缩BMP位图为JPEG会导致精度损失
编码类型
- 定长编码方案:每个字符的编码长度一样,如ASCII码,128个字符,都是用8位二进制码表示的,最高位为0,每个字符的编码与频率无关;
- 变长编码方案:每个字符的编码长度与其出现的频率有关,出现的频率越高,其二进制编码的长度越越短;频率越低,则二进制编码长度越长;
最后总数据的编码长度最短,实现压缩数据。
哈夫曼编码就是一种无损压缩方法,一种变长编码方案
哈夫曼编码
我们这里使用例子来演示
现在存在字符串,长度15,各个字符及频率:A7,B5,C1,D2
AAAABBBCDDBBAAA
需要我们进行二进制编码,明显
采用ASCII码编码,15个字符15字节,编码的长度为 15*8=120位
使用哈夫曼编码
1.我们先得到字符出现的频率集合(也叫权重集合),按从小到大排序
{1,2,5,7}
2.构造哈夫曼树
规则就是
1.在频率集合中找出字符中最小的两个;小的在左边,大的在右边;这两个兄弟组成二叉树。他们的双亲为他们的频率(权值)之和。
2.在频率表中删除此次找到的两个数,并加入此次最小两个数的频率和(把他们的双亲加入,然后排序)。
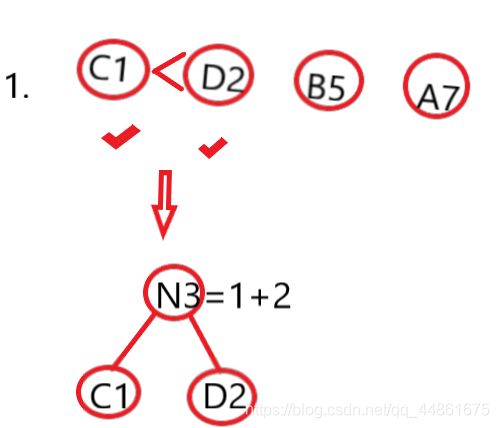
第一步,C1,D2最小 我们将其合成N3,3=1+2,得到的频率排序后的表为
{3,5,7}
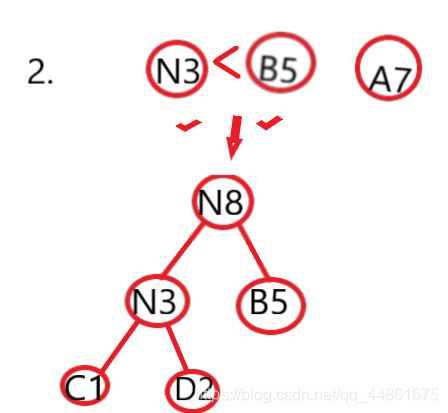
第二步,重复第一步,N3和B5合成N8,8=3+5我们将得到频率排序后的表为
{7,8}
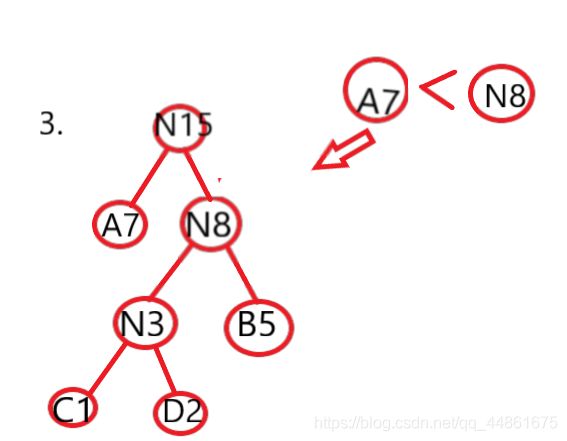
第三步,重复第一步,A7和N8合成N15,15=7+8我们将得到频率排序后的表为
{15}
此时只剩下一个数,我们就结束构造了。
然后
开始哈夫曼编码,左子树为边值0,右子树边值为1,代码里面我们是使用数组保存的
我们得到的哈夫曼树为

得到的哈夫曼编码为(从根结点往下面叶子结点看)
| 元素 | 编码 |
|---|---|
| A | 0 |
| B | 11 |
| C | 100 |
| D | 101 |
所以我们最后的字串编码为 00001111111001011011111000,长度26位
对比ASCII编码,压缩比为 120:26
此时,我们传送任何由ABCD构成的字串,压缩与解压缩都是按照这个编码
我们可以发现,哈夫曼编码得到的编码长度不一,而且,任何一个字符的编码都不是另一字符的编码前缀,所以不会导致识别错,保证了译码的唯一性。
原因 我们这里约定了小的是左子树,大的是右子树,保证了哈夫曼树的唯一性,而且我们的编码元素都是处在叶子结点,结合树的一对多的关系我们就能知道每一个字符的编码唯一,不是其余字符编码的前缀
哈夫曼树
一些二叉树的概念
- 路径长度
从结点X到结点Y的所经过的结点序列叫做从X到Y的一条路径,路径的边数叫做路径长度。从根结点到其余结点的路径长度之和叫做该二叉树的路径长度(Path Length),简称PL。
n个结点的完全二叉树的路径长度最短,长度最短的又不仅仅是完全二叉树。 - 外路径长度
从根结点到所有的叶子结点的路径长度之和为二叉树的外路径长度 - 带权路径长度
因为字符的权值,即出现是频率不同,所有我们使用带权的二叉树来编码,根到X结点的带权路径长度就是从根结点到X结点的路径长度与X结点的权值的乘积,**二叉树的带权外路径长度就是所有的叶子结点的带权路径长度之和(Weight external Path Length)**简称WPL。
哈夫曼树的定义
就是同结点个数的所有的二叉树中,WPL最小的二叉树,HuffmanTree,也叫最优二叉树,所以哈夫曼树不一定是唯一的!
如图,四棵树的WPL都是26.
要想得到唯一一颗哈夫曼树,就要约束左右子树
哈夫曼树构建的约束规则就是:合并结点时,权值较小的结点是左孩子,权值较大的是右孩子。
代码演示
我们现在对ABCDEFGH编码,使用三叉静态链表实现。
1.构建哈夫曼树
//定义哈夫曼树的结构
typedef struct {
int data;//data域存储权值
int parent,lchild,rchild;//双亲与孩子
} HTNode,*HuffmanTree;
/*typedef struct{
string str;
}HuffmanTreenode,*HuffmancodeTree;*/
//哈夫曼树的初始化
int InitHuffmanTree(HuffmanTree H,int weight,int parent,int lchild,int rchild)
{
//HT = (HuffmanTree)malloc(n*sizeof(HTNode));//空间分配_我们通过createHuffmanTree来调用,无须分配
H->lchild=lchild;
H->rchild=rchild;
H->parent =parent;
H->data = weight;
}
//建立哈夫曼树!
void CreateHuffmanTree(HuffmanTree &HT,int n,int *W)
{
//叶子结点的初始化,相当于n棵树,每颗树只有一个结点,那么最后构造过程总的结点个数为:2*n-1
//n-1+n = 2*n-1
HT = (HuffmanTree)malloc((2*n-1)*sizeof(HTNode));//n个叶子结点的哈夫曼树结点是2n-1;
for(int i=0; i<n; i++) {
InitHuffmanTree(HT+i,W[i],-1,-1,-1);//初始化-1
}
//开始寻找最小的两个叶子结点,构造哈夫曼树
for(int i=n; i<2*n-1; i++) { //我们构造n-1个度为2的结点
int min1=65522,min2=min1;//这里的两个数分别代表第一小,第二小
int x1=-1,x2=-1;//用来记录下标
for(int j=0; j<i; j++) {
if((HT+j)->parent==-1)//表示叶子结点没有父母
if((HT+j)->data<min1) {
min2=min1;
min1=(HT+j)->data;
x2=x1;
x1=j;
} else if((HT+j)->data<min2) {
min2=(HT+j)->data;
x2=j;
}
}
//合并两个叶子,让他们有同一个双亲
(HT+x1)->parent =i;
(HT+x2)->parent =i;
//然后我们让HT[i]指向这两个孩子,为了后来的逆序哈夫曼编码
InitHuffmanTree(HT+i,min2+min1,-1,x1,x2) ;//父结点构造
}
}
//完成哈夫曼树的生成;
2.哈夫曼树的编码
//获得哈夫曼编码,n是指叶子个数,path是我们要获得的字符的编码
void HuffmanTreeCode(HuffmanTree HT,char *str,int n,int path,int &e)
{
int i=0,j=0,m=0;
int child =path;//假设我们现在在叶子结点为child索引的地方,如1
int parent = (HT+child)->parent;//获取第一个叶子结点的父节点 的值
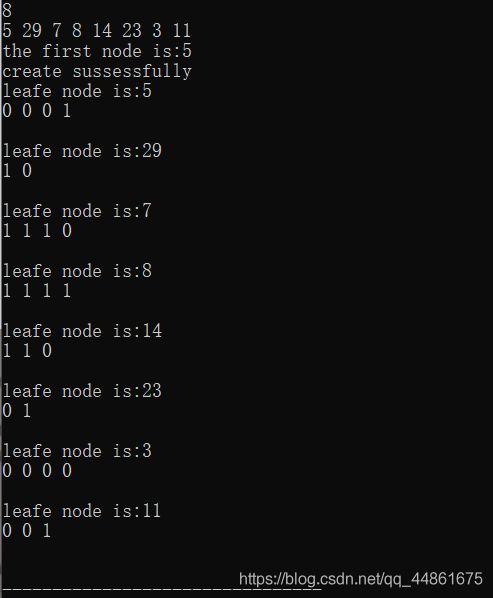
//printf("leafe node is:%d \n",(HT+child)->data);
//开始逆序寻找根节点,及生成编码
for(i=n-1; parent!=-1; i--) //当前结点不是根结点 ,逆序
if((HT+parent)->lchild==child) { //他的双亲指向的左孩子是不是我们当前遍历的这个叶子
str[j++] = '0';
child = parent;///此时parent!=-1 ,表示还有父节点
parent=(HT+child)->parent;
} else {
str[j++] = '1';//实现编码
child = parent;
parent=(HT+child)->parent;
}
e=j;//表示一个叶子结点的编码结束
}//一次获取一个字符的编码,时间复杂度为O(n)
for(int k=0; k<n; k++) {
HuffmanTreeCode(HT,str,n,k,e) ;
for(int j=e-1;j>=0 ; j--)
printf("%c ",str[j]);
printf("\n\n");
}
#include "stdio.h"
#include "malloc.h"
#include "string.h"
#include "string"
//定义哈曼夫树的结构
typedef struct {
int data;//data域存储权值
int parent,lchild,rchild;//双亲与孩子
} HTNode,*HuffmanTree;
/*typedef struct{
string str;
}HuffmanTreenode,*HuffmancodeTree;*/
//哈曼夫树的初始化
void InitHuffmanTree(HuffmanTree H,int weight,int parent,int lchild,int rchild)
{
//HT = (HuffmanTree)malloc(n*sizeof(HTNode));//空间分配
H->lchild=lchild;
H->rchild=rchild;
H->parent =parent;
H->data = weight;
}
//建立哈夫曼树!
void CreateHuffmanTree(HuffmanTree &HT,int n,int *W)
{
//叶子结点的初始化,相当于n棵树,每颗树只有一个结点,那么最后构造过程总的结点个数为:2*n-1
//n-1+n = 2*n-1
HT = (HuffmanTree)malloc((2*n-1)*sizeof(HTNode));//n个叶子结点的哈夫曼树结点是2n-1;
for(int i=0; i<n; i++) {
InitHuffmanTree(HT+i,W[i],-1,-1,-1);//初始化-1
}
//开始寻找最小的两个叶子结点,构造哈夫曼树
for(int i=n; i<2*n-1; i++) { //我们构造n-1个度为2的结点
int min1=65522,min2=min1;//这里的两个数分别代表第一小,第二小
int x1=-1,x2=-1;//用来记录下标
for(int j=0; j<i; j++) {
if((HT+j)->parent==-1)//表示叶子结点没有父母
if((HT+j)->data<min1) {
min2=min1;
min1=(HT+j)->data;
x2=x1;
x1=j;
} else if((HT+j)->data<min2) {
min2=(HT+j)->data;
x2=j;
}
}
//合并两个叶子,让他们有同一个双亲
(HT+x1)->parent =i;
(HT+x2)->parent =i;
//然后我们让HT[i]指向这两个孩子,为了后来的逆序哈夫曼编码
InitHuffmanTree(HT+i,min2+min1,-1,x1,x2) ;//父结点构造
}
}
//完成哈夫曼树的生成;
//获得哈夫曼编码,n是指叶子个数,path是我们要获得的字符的编码
void HuffmanTreeCode(HuffmanTree HT,char *str,int n,int path,int &e)
{
int i=0,j=0,m=0;
int child =path;//假设我们现在在叶子结点为child索引的地方,如1
int parent = (HT+child)->parent;//获取第一个叶子结点的父节点 的值
//printf("leafe node is:%d \n",(HT+child)->data);
//开始逆序寻找根节点,及生成编码
for(i=n-1; parent!=-1; i--) //当前结点不是根结点 ,逆序
if((HT+parent)->lchild==child) { //他的双亲指向的左孩子是不是我们当前遍历的这个叶子
str[j++] = '0';
child = parent;///此时parent!=-1 ,表示还有父节点
parent=(HT+child)->parent;
} else {
str[j++] = '1';//实现编码
child = parent;
parent=(HT+child)->parent;
}
e=j;//表示一个叶子结点的编码结束
}
int main()
{
int i,n;
int *w,e;
HuffmanTree HT;
//printf("Node Number:");
scanf("%d",&n); //权值个数
w=(int *)malloc(n*sizeof(int)); //权值数组
//printf("Input weights:");
for ( i=0; i<n; i++) //录入权值
scanf("%d",&w[i]);
CreateHuffmanTree(HT,n,w);
//printf("the first node is:%d\n",HT->data);
//printf("create sussessfully\n");
//定义一个数组存储哈夫曼编码
char str[n];
for(int k=0; k<n; k++) {
HuffmanTreeCode(HT,str,n,k,e) ;
for(int j=e-1;j>=0 ; j--)
printf("%c",str[j]);
printf("\n");
}
free(HT);
return 0;
}//main