【深度学习】《PyTorch入门到项目实战》（十一）：卷积层

【深度学习】：《PyTorch入门到项目实战》（十一）：卷积层

• ✨本文收录于【深度学习】：《PyTorch入门到项目实战》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 个人主页：JoJo的数据分析历险记
• 个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 如果文章对你有帮助，欢迎✌关注、点赞、✌收藏、订阅专栏
• 参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。
• 视频：动手学深度学习
• 教材：动手学深度学习

卷积神经网络（CNN）：卷积层实现

之前已经介绍了基本的神经网络知识以及一些处理过拟合欠拟合的概念。现在我们正式进入卷积神经网络的学习。CNN是⼀类强⼤的、为处理图像数据⽽设计的神经⽹络。基于卷积神经⽹络架构的模型在计算机视觉领域中已经占主导地位，当今⼏乎所有的图像识别、⽬标检测或语义分割相关的学术竞赛和商业应⽤都以这种⽅法为基础。对于计算机视觉而言，面临的一个重大挑战就是数据的输入可能会很大。例如，我们有一张64$\times$ 64的图片，假设通道数为3，那么它是数据量相当于是一个$64\times 64\times 3=12288$的特征向量。当我们要操作更大的图片时候，需要进行卷积计算，它是卷积神经网络中非常重要的一部分。

1.引入

让我们举个例子，假设给了我们这样一张图片

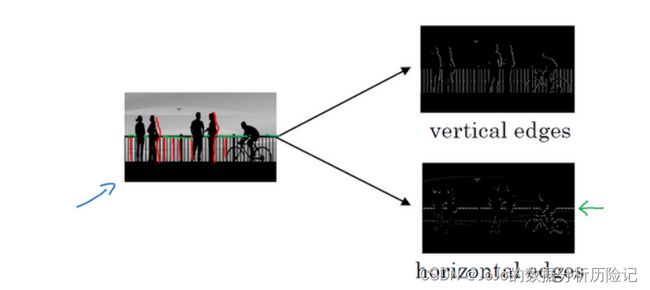
让电脑去搞清楚这张照片里有什么物体，我们可能做的第一件事是检测图片中的垂直边缘。比如说，在这张图片中的栏杆就对应垂直线，与此同时，这些行人的轮廓线某种程度上也是垂线，这些线是垂直边缘检测器的输出。同样，我们可能也想检测水平边缘，比如说这些栏杆就是很明显的水平线，所以如何在图像中检测这些边缘？
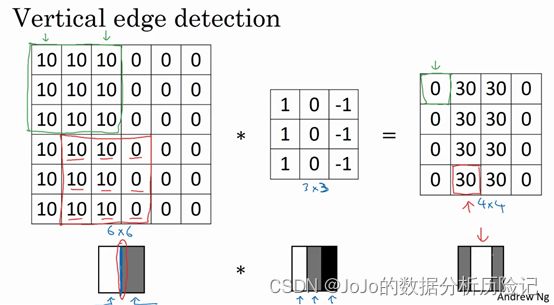
我们可以构建一个$3\times 3$的矩阵，我们也称为过滤器或者核函数(kernel)。下面我们通过Andrew Ng的解释来看看为什么这个能做边缘检测？

上图一个简单的6×6图像，左边的一半是10，右边一般是0。如果你把它当成一个图片，左边那部分看起来是白色的，像素值10是比较亮的像素值，右边像素值比较暗，我使用灰色来表示0，尽管它也可以被画成黑的。图片里，有一个特别明显的垂直边缘在图像中间，这条垂直线是从黑到白的过渡线，或者从白色到深色。所以，当我们用一个3×3过滤器进行卷积运算的时候，这个3×3的过滤器结果，在左边有明亮的像素，然后有一个过渡，0在中间，然后右边是深色的。卷积运算后，我们得到的是右边的矩阵。还有许多其他的边缘检测方法，关于具体的计算机视觉任务，我们在后续介绍，接下来我们来看看卷积具体是怎么计算的

2.卷积运算

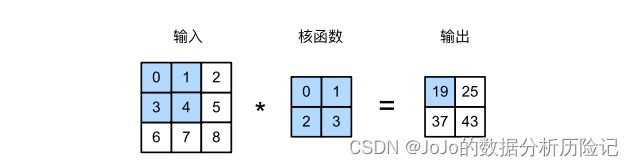
下面我们来看看卷积具体是怎么计算的，给一个输入矩阵和一个核函数，我们将从输入特征的左上角开始与核函数求内积，然后在进行滑动窗口，求下一个内积。得到我们的输出,具体计算如下
$$\begin{gathered} 0\times 0+1\times 1+3\times 2+4\times 3=19 \\ 1\times 0+1\times 2+4\times 2+3\times 5=25 \\ 3\times 0+4\times 1+6\times 2+7\times 3=37 \\ 4\times 0+1\times 5+2\times 7+3\times 8=43 \end{gathered}$$

可以看出，通过卷积计算后，我们的原始数据特征变小了。假设输入矩阵为$n\times n$,核函数（Kernel）为$f\times f$，通常核是一个方阵形式。那么得到的输出结果为$(n-f+1)\times (n-f+1)$

3 代码实现

3.1下面我们来简单的实现卷积运算

"""导入相关库"""
import torch
from torch import nn

def corr2d(X,K):
    """定义卷积运算"""
    h, w = K.shape#核的shape，通常这里的h和w是相等的
    Y = torch.zeros((X.shape[0]-h+1, X.shape[1]-w+1))#初始化输出结果
    for i in range(Y.shape[0]):#输出矩阵的第i行
        for j in range(Y.shape[1]):#输出矩阵的第j列
            Y[i,j] = (X[i:i+h,j:j+w] * K).sum()#计算对应内积
    return Y 

下面我们来测试一下是否正确

X = torch.Tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
K = torch.Tensor([[0.0,1.0],[2.0,3.0]])
corr2d(X,K)

可以看出和我们之前的结果一致.

3.2 构造卷积层

之前我们介绍了如何构造线性层，激活函数，以及drop-out，类似的，我们通过定义一个类来定义卷积层

class Conv2D(nn.Module):
    """定义二维卷积层"""
    def __init__(self, kernel_size):#定义核函数的大小，这是一个超参数
        super().__init__()
        self.weight = nn.Parameter(torch.rand(Kernel_size))#学习的参数
        self.bias = nn.Parameter(torch.zeros(1))#学习的参数
    def forward(self, x):
        return corr2d(x,self.weight)+self.bias#计算卷积结果

3.3 检测图像颜色边缘

首先我们定义一个X，假设1代表灰色，0代表白色

X = torch.ones(6,6)
X[:,2:4] = (0.0)
X

下面我们进行边缘检测，在这里我们构造一个$1\times 2$的核函数

K = torch.tensor([[1.0,-1.0]])
K

Y = corr2d(X,K)
Y

其中，1表示从灰色到白色的垂直边缘，-1表示从白色到黑色的垂直边缘

上述定义的核只能检测垂直边缘，现在假设我们对X进行转置，我们想要检测水平边缘

Y = corr2d(X.t(),K)
Y

可以看见此时的核函数（Kernel）不能够检测水平边缘，我们需要对kernel也进行转置

Y = corr2d(X.t(),K.t())
Y

3.4 学习卷积核

刚刚是我们自己定义的卷积核，但是当如果我们需要进行更复杂的计算时，直接定义卷积核是很困难的，我们下面来看看能不能通过输入和输出矩阵来学习到我们的卷积核，这里我们定义损失函数为Y和卷积层输出的平方误差。

# 构造⼀个⼆维卷积层，它具有1个输出通道和形状为（2，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
# 这个⼆维卷积层使⽤四维输⼊和输出格式（批量⼤⼩、通道、⾼度、宽度），
# 其中批量⼤⼩和通道数都为1
X = X.reshape((1, 1, 6, 6))
Y = Y.reshape((1, 1, 6, 5))
lr = 3e-2 # 学习率
for i in range(10):
    Y_hat = conv2d(X)#计算卷积
    l = (Y_hat - Y) ** 2#损失函数
    conv2d.zero_grad()
    l.sum().backward()#反向传播计算梯度
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')

可以看出经过10次迭代后，误差已经较低了，我们下面看看学习到的卷积核参数

conv2d.weight

结果和我们之前定义的1，-1基本接近。
本章介绍了如何进行卷积计算以及定义卷积层，后续介绍padding、多维卷积、池化层等。

本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！