100个python算法超详细讲解：魔方阵

【100个python算法超详细讲解】@谷哥技术

1．问题描述
编写程序，实现如图8.13所示的5-魔方阵。
2．问题分析
所谓“n-魔方阵”，指的是使用l～n 2 共n 2 个自然数排列成一个n×n的方阵，其中n
为奇数。该方阵的每行、每列以及对角线元素之和都相等，并为一个只与n有关的常
数，该常数为n×(n 2 +1)/2。
例如，图8.13所示的5-魔方阵，其第一行、第一列以及主对角线上各元素之和如
下。

第一行元素之和：17+24+1+8+15=65
第一列元素之和：17+23+4+10+11=65
主对角线上元素之和：17+5+13+21+9=65
而n×(n 2 +1)/2=5×(5 2 +1)/2=65
可以验证，5-魔方阵中其余各行、各列以及副对角线上的元素之和也都为65。
假定阵列的行列下标都从0开始，则魔方阵的生成方法如下：
1）在第0行中间置1，并对从2开始的其余n 2 -1个数依次按下面2～5所列规则存
放。
2）假定当前数的下标为(i,j)，则下一个数的放置位置为当前位置的右上方，即
下标为(i-1,j+1)的位置。
3）如果当前数在第0行，即i-1小于0，则将下一个数放在最后一行的下一列上，
即下标为(n-1,j+1)的位置。
4）如果当前数在最后一列上，即j+1大于n-1，则将下一个数放在上一行的第一
列上，即下标为(i-1,0)的位置。
5）如果当前数是n的倍数，则将下一个数直接放在当前位置的正下方，即下标
为(i+1,j)的位置。
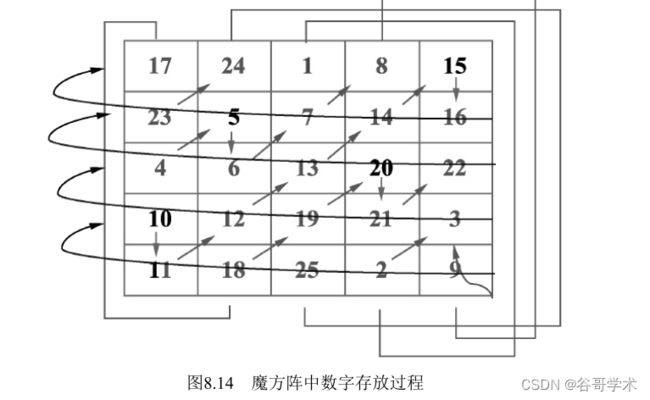
按照上面的规则，5-魔方阵中数字的存放过程如图8.14所示。

 

3．算法设计
在设计算法时采用了下面的一些方法：
1）定义array()函数，该函数根据输入的n值，生成并显示一个魔方阵，当发现n
不是奇数时，就加1使之成为奇数。
2）显然我们应该使用数组来表示魔方阵。
4．确定程序框架
（1）定义数组
要生成n阶魔方阵，共需要存入n 2 个自然数，在程序中首先要为这n 2 个自然数进
行初始化定义，代码如下：
max = n * n
mtrx = [1] * max
（2）生成魔方阵
生成魔方阵时按照在问题分析中介绍的生成规律，需要考虑几种不同情况，这
几种情况在代码中都应该体现出来。按照生成规律，首先应该将自然数1存入数组
mtrx中，然后从2开始再依次确定每个数的存放位置。生成魔方阵的代码如下：

mtrx[n // 2] = 1 # 将1存入数组
i = 0 # 自然数1所在行
j = n // 2 # 自然数1所在列
# 从2开始确定每个数的存放位置
for num in range(2, max + 1):
i = i - 1
j = j + 1
if (num - 1) % n == 0: # 当前数是n的倍数
i = i + 2
j = j - 1
if i < 0: # 当前数在第0行
i = n - 1
if j > n - 1: # 当前数在最后一列，即n-1列
j = 0
no = i * n + j # 找到当前数在数组中存放的位置

 5．完整的程序
根据上面的分析，编写程序如下：

#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 魔方阵
def array(n):
if n % 2 == 0: # n是偶数，则加1使其变为奇数
n = n + 1
max = n * n
mtrx = [1] * max
mtrx[n // 2] = 1 # 将1存入数组
i = 0 # 自然数1所在行
j = n // 2 # 自然数1所在列
# 从2开始确定每个数的存放位置
for num in range(2, max + 1):
i = i - 1
j = j + 1
if (num - 1) % n == 0: # 当前数是n的倍数
i = i + 2
j = j - 1
if i < 0: # 当前数在第0行
i = n - 1
if j > n - 1: # 当前数在最后一列，即n-1列
j = 0
no = i * n + j # 找到当前数在数组中存放的位置
mtrx[no] = num
# 打印生成的魔方阵
生成的 魔方阵为
print("生成的%d-魔方阵为：" %n, end="")
no = 0
for i in range(0, n):
print()
for j in range(0, n):
print("%3d" %mtrx[no], end=" ")
no += 1
print()
if __name__ == "__main__":
n = int(input("请输入n值："))
array(n) # 调用array()函数

6．运行结果
在PyCharm下运行程序，屏幕上提示“请输入n值：”，输入5，则可以正确打印出
5-魔方阵，运行结果如图8.15所示。

7．问题拓展
在解决该问题时，我们使用一维数组来生成魔方阵。这里再给出直接使用二维
数组来生成5-魔方阵的程序，以便于读者进行比较。
直接使用二维数组生成5-魔方阵的代码如下：

#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 魔方矩阵
if __name__ == "__main__":
N = 5
a = [[0] * 5 for i in range(5)] # 定义一个5×5的二维数组
i = 0 # 自然数1的行标
j = N // 2 # 自然数1的列标
t = N - 1
k = 1
while k <= (N * N): # 变量k控制循环和自然数
a[i][j] = k
变量 保存新的行
x = i # 变量x保存新的行
y = j # 变量y保存新的列
if i == 0:
i = t # 当前数在第0行，则下一个数在最后一行
else:
i = i - 1 # 产生行，非第0行，则取下一列
if j != t:
j = j + 1 # 产生列，非最后列，则取下一列
else:
j = 0 # 当前数在最后一列，则下一个数在第一列
if a[i][j] != 0:
i = x + 1
j = y
k += 1
# 打印生成的魔方阵
print("生成的5-魔方阵为：", end="")
for i in range(N):
print()
for j in range(N):
print("%3d " %a[i][j], end=" ")
print()

 上面的代码定义了二维数组a[N][N]，其中N是字符常量，表示数值5，因此数组
a[N][N]可以存放一个5-魔方阵。接着找到自然数所在位置的行标和列标，下面就开
始将N×N（即25）个数存入二维数组a。
将数存入二维数组a使用的是while循环，循环变量为k值，共循环25次，存入时
要遵循魔方阵的存入规则。每次循环时，先将当前数k存入二维数组的指定元素a[i][j]
中，然后判断下一个数的存放位置，即i和j的值。加粗的代码是表示如果按魔方阵的
存入规则得出的位置已经被占用，则下一个自然数应该存放在当前数的下一行上，
但是与当前数在同一列上。这与使用魔方阵生成规则中的第5条“如果当前数是n的倍
数，则将下一个数直接放在当前位置的正下方，即下标为(i+1,j)的位置。”找到的位
置是相同的。
运行程序，结果如图8.16所示。由图8.16中可以看出，打印出的5-魔方阵与图
8.15中打印出的5-魔方阵是完全相同的。