贝叶斯优化神经网络参数
The purpose of this work is to optimize the neural network model hyper-parameters to estimate facies classes from well logs. I will include some codes in this paper but for a full jupyter notebook file, you can visit my Github.
这项工作的目的是优化神经网络模型的超参数,以从测井中估计相类。 我将在本文中包括一些代码,但要获取完整的jupyter笔记本文件,您可以访问我的Github 。
note: if you are new in TensorFlow, its installation elaborated by Jeff Heaton.
注意:如果您是TensorFlow的新手,那么其安装将由Jeff Heaton进行详细说明。
In machine learning, model parameters can be divided into two main categories:1- Trainable parameters: such as weights in neural networks learned by training algorithms and the user does not interfere in the process,2- Hyper-parameters: users can set them before training operation such as learning rate or the number of dense layers in the model.Selecting the best hyper-parameters can be a tedious task if you try it by hand and it is almost impossible to find the best ones if you are dealing with more than two parameters.One way is to divide each parameter into a valid evenly range and then simply ask the computer to loop for the combination of parameters and calculate the results. The method is called Grid Search. Although it is done by machine, it will be a time-consuming process. Suppose you have 3 hyper-parameters with 10 possible values in each. In this approach, you will run 10³ neural network models (even with reasonable training datasets size, this task is huge).Another way is a random search approach. In fact, instead of using organized parameter searching, it will go through a random combination of parameters and look for the optimized ones. You may estimate that chance of success decreases to zero for larger hyper-parameter tunings.
在机器学习中,模型参数可以分为两大类: 1-可 训练参数 :例如通过训练算法学习的神经网络权重,并且用户不会干扰过程; 2- 超参数:用户可以在设置参数之前训练操作,例如学习率或模型中的密集层数。如果您手动尝试选择最佳超参数可能是一项繁琐的任务,并且如果您要处理的参数过多,则几乎找不到最佳参数两个参数。一种方法是将每个参数平均划分为有效范围,然后简单地让计算机循环以获取参数组合并计算结果。 该方法称为“ 网格搜索” 。 尽管它是由机器完成的,但这将是一个耗时的过程。 假设您有3个超参数,每个参数都有10个可能的值。 在这种方法中,您将运行10³神经网络模型(即使具有合理的训练数据集大小,此任务也非常艰巨)。另一种方法是随机搜索方法。 实际上,它会使用参数的随机组合并寻找经过优化的参数,而不是使用有组织的参数搜索。 您可能会估计,对于较大的超参数调整,成功的机会将减少为零。
Scikit-Optimize, skopt, which we will use here to the facies estimation task, is a simple and efficient library to minimize expensive noisy black-box functions. Bayesian optimization constructs another model of search-space for parameters. Gaussian Process is one kind of these models. This generates an estimate of how model performance varies with hyper-parameter changes.
Scikit-Optimize skopt是一个简单而有效的库,可最大程度地减少昂贵的嘈杂黑盒功能,我们将在此处将其用于相估计任务。 贝叶斯优化为参数构造了另一种搜索空间模型。 高斯过程就是这些模型中的一种。 这样就可以估算模型性能如何随超参数变化而变化。
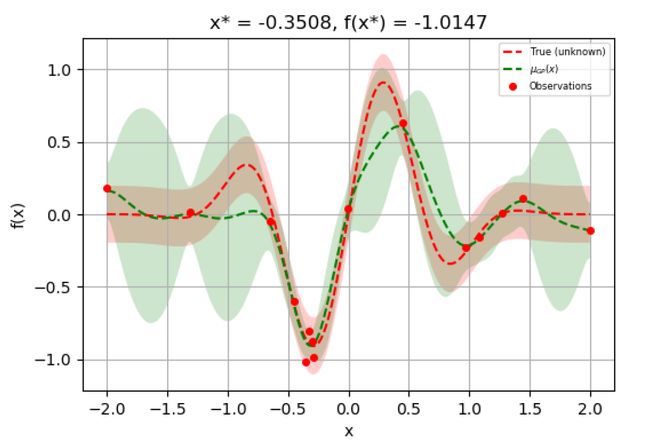
As we see in the picture, the true objective function(red dash line) is surrounded by noise (red shade). The red line shows how scikit optimize sampled the search space for hyper-parameters(one dimension). Scikit-optimize fills the area between sample points with the Gaussian process (green line) and estimates true real fitness value. In the areas with low samples or lack(like the left side of the picture between two red samples), there is great uncertainty (big difference between red and green lines causing big uncertainty green shade area such as two standard deviations uncertainty).In this process, then we ask a new set of hyper-parameter to explore more search space. In the initial steps, it goes with sparse accuracy but in later iterations, it focuses on where sampling points are more with the good agreement of fitness function with true objective function(trough area in the graph).For more study, you may refer to Scikit Optimize documentation.
如图所示,真正的目标函数(红色虚线)被噪声(红色阴影)包围。 红线显示scikit如何优化对超参数(一维)的搜索空间进行采样。 Scikit优化使用高斯过程(绿线)填充采样点之间的区域,并估算真实的实际适应度值。 在样本较少或不足的区域(例如两个红色样本之间的图片左侧),存在很大的不确定性(红色和绿色线条之间的差异很大,导致绿色阴影区域的不确定性较大,例如两个标准偏差不确定性)。过程,然后我们要求使用一组新的超参数来探索更多的搜索空间。 在最初的步骤中,它具有稀疏的准确性,但是在以后的迭代中,它着重于采样点更多,适应度函数与真实目标函数(图中的谷值区域)具有良好一致性的地方。更多的研究,您可以参考Scikit优化文档 。
Data ReviewThe Council Grove gas reservoir is located in Kansas. From this carbonate reservoir, nine wells are available. Facies are studied from core samples in every half foot and matched with logging data in well location. Feature variables include five from wireline log measurements and two geologic constraining variables that are derived from geologic knowledge. For more detail refer here. For the dataset, you may download it from here. The seven variables are:
数据审查 Council Grove储气库位于堪萨斯州。 从该碳酸盐岩储层中可获得九口井。 从每半英尺的岩心样本中研究岩相,并与井眼位置的测井数据相匹配。 特征变量包括来自测井测井的五个变量和来自地质知识的两个地质约束变量。 有关更多详细信息,请参见此处 。 对于数据集,您可以从此处下载。 七个变量是:
GR: this wireline logging tools measure gamma emission
GR :此电缆测井工具可测量伽马辐射
ILD_log10: this is resistivity measurement
ILD_log10 :这是电阻率测量
PE: photoelectric effect log
PE :光电效应记录
DeltaPHI: Phi is a porosity index in petrophysics.
DeltaPHI :Phi是岩石物理学中的Kong隙度指数。
PNHIND: Average of neutron and density log.
PNHIND :中子和密度对数的平均值。
NM_M:nonmarine-marine indicator
NM_M :非海洋-海洋指示器
RELPOS: relative position
RELPOS :相对位置
The nine discrete facies (classes of rocks) are:
九个离散相(岩石类别)为:
(SS) Nonmarine sandstone
(SS)浅海砂岩
(CSiS) Nonmarine coarse siltstone
(CSiS)浅海粗粉砂岩
(FSiS) Nonmarine fine siltstone
(FSiS)船用细粉砂岩
(SiSH) Marine siltstone and shale
(SiSH)海洋粉砂岩和页岩
(MS) Mudstone (limestone)
(MS)泥岩(石灰石)
(WS) Wackestone (limestone)
(WS) Wackestone(石灰石)
(D) Dolomite
(D)白云石
(PS) Packstone-grainstone (limestone)
(PS) Packstone-grainstone(石灰石)
(BS) Phylloid-algal bafflestone (limestone)
(BS) Phylloid-alal挡板石(石灰石)
After reading the dataset into python, we can keep one well data as a blind set for future model performance examination. We also need to convert facies numbers into strings in the dataset. Refer to the full notebook.
将数据集读入python后,我们可以保留一个井数据作为盲集,以供将来进行模型性能检查。 我们还需要将相序数字转换为数据集中的字符串。 请参阅完整的笔记本。
df = pd.read_csv(‘training_data.csv’)
blind = df[df['Well Name'] == 'SHANKLE']
training_data = df[df['Well Name'] != 'SHANKLE']Feature EngineeringFacies classes should be converted to dummy variable in order to use in neural network:
为了将其用于神经网络,应将特征工程相类转换为虚拟变量:
dummies = pd.get_dummies(training_data[‘FaciesLabels’])
Facies_cat = dummies.columns
labels = dummies.values # target matirx# select predictors
features = training_data.drop(['Facies', 'Formation', 'Well Name', 'Depth','FaciesLabels'], axis=1)预处理(使标准) (Preprocessing (make standard))
As we are dealing with various range of data, to make network efficient, let’s normalize it.
当我们处理各种数据时,为了使网络高效,我们将其标准化。
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(features)
scaled_features = scaler.transform(features)#Data split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
scaled_features, labels, test_size=0.2, random_state=42)超参数 (Hyper-Parameters)
In this work, we will predict facies from well logs using deep learning in Tensorflow. There several hyper-parameters that we may adjust for deep learning. I will try to find out the optimized parameters for:
在这项工作中,我们将使用Tensorflow中的深度学习来预测测井相。 我们可以为深度学习调整一些超参数。 我将尝试找出以下方面的优化参数:
Learning rate
学习率
Number of dense layers
致密层数
Number of nodes for each layer
每层的节点数
Which activation function: ‘relu’ or sigmoid
哪个激活功能:“ relu”或Sigmoid
To elaborate in this search dimension, we will use scikit-optimize(skopt) library. From skopt, real function will define our favorite range(lower bound = 1e-6, higher bound = 1e-1) for learning rate and will use logarithmic transformation. The search dimension for the number of layers (we look between 1 to 5) and each layer’s node amounts(between 5 to 512) can be implemented with Integer function of skopt.
为了详细说明此搜索维度,我们将使用scikit-optimize(skopt)库。 从skopt中,实函数将定义我们喜欢的范围(下限= 1e-6,上界= 1e-1)以提高学习率,并将使用对数转换。 可以使用skopt的Integer函数实现搜索层数(我们在1到5之间)和每个层的节点数量(在5到512之间)的搜索维度。
dim_learning_rate = Real(low=1e-6, high=1e-1, prior='log-uniform',
name='learning_rate')dim_num_dense_layers = Integer(low=1, high=10, name='num_dense_layers')dim_num_dense_nodes = Integer(low=5, high=512, name='num_dense_nodes')For activation algorithms, we should use categorical function for optimization.
对于激活算法,我们应该使用分类函数进行优化。
dim_activation = Categorical(categories=['relu', 'sigmoid'],
name='activation')Bring all search-dimensions into a single list:
将所有搜索维度合并到一个列表中:
dimensions = [dim_learning_rate,
dim_num_dense_layers,
dim_num_dense_nodes,
dim_activation]If you already worked with deep learning for a specific project and found your hyper-parameters by hand for that project, you know how hard it is to optimize. You may also use your own guess (like mine as default) to compare the results with the Bayesian tuning approach.
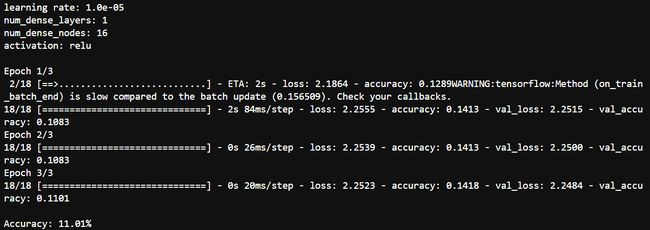
如果您已经为特定项目进行了深度学习,并且手动找到了该项目的超参数,那么您就会知道优化的难度。 您也可以使用自己的猜测(例如默认为我的)将结果与贝叶斯调整方法进行比较。
default_parameters = [1e-5, 1, 16, ‘relu’]超参数优化 (Hyper-Parameter Optimization)
建立模型 (Create Model)
Like some examples developed by Tneseflow, we also need to define a model function first. After defining the type of model(Sequential here), we need to introduce the data dimension (data shape) in the first line. The number of layers and activation types are those two hyper-parameters that we are looking for to optimize. Softmax activation should be used for classification problems. Then another hyper-parameter is the learning rate which should be defined in the Adam function. The model should be compiled considering that loss function should be ‘categorical_crossentropy’ as we are dealing with the classification problems (facies prediction).
像Tneseflow开发的一些示例一样,我们还需要首先定义一个模型函数。 定义模型的类型(此处为顺序)后,我们需要在第一行中介绍数据维度(数据形状)。 层数和激活类型是我们要优化的那两个超参数。 Softmax激活应用于分类问题。 然后另一个超参数是学习率,该学习率应在亚当函数中定义。 在处理分类问题(相预测)时,应考虑损失函数应为“ categorical_crossentropy”,对模型进行编译。
def create_model(learning_rate, num_dense_layers,
num_dense_nodes, activation):
model = Sequential()
model.add(InputLayer(input_shape=(scaled_features.shape[1])))
for i in range(num_dense_layers):
name = 'layer_dense_{0}'.format(i+1)
# add dense layer
model.add(Dense(num_dense_nodes,
activation=activation,
name=name))
# use softmax-activation for classification.
model.add(Dense(labels.shape[1], activation='softmax'))
# Use the Adam method for training the network.
optimizer = Adam(lr=learning_rate)
#compile the model so it can be trained.
model.compile(optimizer=optimizer,
loss='categorical_crossentropy',
metrics=['accuracy'])
return model训练和评估模型 (Train and Evaluate the Model)
This function aims to create and train a network with given hyper-parameters and then evaluate model performance with the validation dataset. It returns fitness value, negative classification accuracy on the dataset. It is negative because skopt performs minimization rather than maximization.
此功能旨在创建和训练具有给定超参数的网络,然后使用验证数据集评估模型性能。 它在数据集上返回适应度值,负分类精度。 这是负面的,因为skopt会执行最小化而不是最大化。
@use_named_args(dimensions=dimensions)def fitness(learning_rate, num_dense_layers,
num_dense_nodes, activation):
""" Hyper-parameters: learning_rate: Learning-rate for the optimizer. num_dense_layers: Number of dense layers. num_dense_nodes: Number of nodes in each dense layer. activation: Activation function for all layers. """
# Print the hyper-parameters.
print('learning rate: {0:.1e}'.format(learning_rate))
print('num_dense_layers:', num_dense_layers)
print('num_dense_nodes:', num_dense_nodes)
print('activation:', activation)
print()
# Create the neural network with these hyper-parameters.
model = create_model(learning_rate=learning_rate,
num_dense_layers=num_dense_layers,
num_dense_nodes=num_dense_nodes,
activation=activation)
# Dir-name for the TensorBoard log-files.
log_dir = log_dir_name(learning_rate, num_dense_layers,
num_dense_nodes, activation)
# Create a callback-function for Keras which will be
# run after each epoch has ended during training.
# This saves the log-files for TensorBoard.
# Note that there are complications when histogram_freq=1.
# It might give strange errors and it also does not properly
# support Keras data-generators for the validation-set.
callback_log = TensorBoard(
log_dir=log_dir,
histogram_freq=0,
write_graph=True,
write_grads=False,
write_images=False)
# Use Keras to train the model.
history = model.fit(x= X_train,
y= y_train,
epochs=3,
batch_size=128,
validation_data=validation_data,
callbacks=[callback_log])
# Get the classification accuracy on the validation-set
# after the last training-epoch.
accuracy = history.history['val_accuracy'][-1]
# Print the classification accuracy.
print()
print("Accuracy: {0:.2%}".format(accuracy))
print()
# Save the model if it improves on the best-found performance.
# We use the global keyword so we update the variable outside
# of this function.
global best_accuracy
# If the classification accuracy of the saved model is improved ...
if accuracy > best_accuracy:
# Save the new model to harddisk.
model.save(path_best_model)
# Update the classification accuracy.
best_accuracy = accuracy
# Delete the Keras model with these hyper-parameters from memory.
del model
# Clear the Keras session, otherwise it will keep adding new
# models to the same TensorFlow graph each time we create
# a model with a different set of hyper-parameters.
K.clear_session()
# NOTE: Scikit-optimize does minimization so it tries to
# find a set of hyper-parameters with the LOWEST fitness-value.
# Because we are interested in the HIGHEST classification
# accuracy, we need to negate this number so it can be minimized.
return -accuracy# This function exactly comes from :Hvass-Labs, TensorFlow-Tutorialsrun this:
运行这个:
fitness(x= default_parameters)运行超参数优化 (Run Hyper-Parameter Optimization)
We already checked the default hyper-parameter performance. Now we can examine Bayesian optimization from scikit-optimize library. Here we use 40 runs for fitness function, though it is an expensive operation and needs to used carefully with datasets.
我们已经检查了默认的超参数性能。 现在我们可以从scikit-optimize库检查贝叶斯优化。 在这里,我们使用40个运行来进行适应度函数计算,尽管这是一项昂贵的操作,并且需要谨慎使用数据集。
search_result = gp_minimize(func=fitness,
dimensions=dimensions,
acq_func='EI', # Expected Improvement.
n_calls=40,
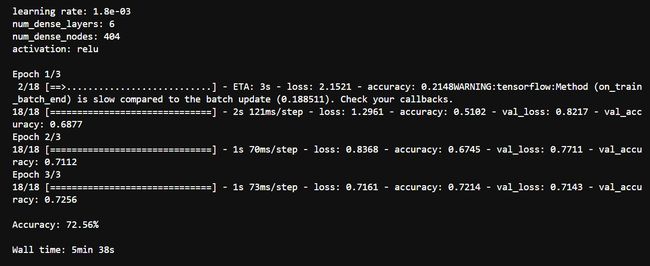
x0=default_parameters)just some last runs shows below:
下面是一些最后的运行:
进度可视化 (Progress visualization)
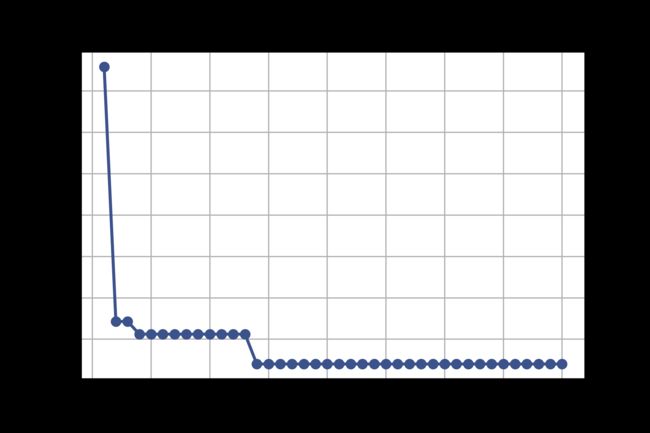
Using plot_convergence function of skopt, we may see the optimization progress and the best fitness value found on y-axis.
使用skopt的plot_convergence函数,我们可以在y轴上看到优化进度和最佳适应度值。
plot_convergence(search_result) # plt.savefig("Converge.png", dpi=400)最佳超参数 (Optimal Hyper-Parameters)
Using the serach_result function, we can see the best hyper-parameter that Bayesian-optimizer generated.
使用serach_result函数,我们可以看到贝叶斯优化器生成的最佳超参数。
search_result.xOptimized hyper-parameters are in order: Learning rate, number of dense layers, number of nodes in each layer, and the best activation function.
优化的超参数按顺序排列:学习率,密集层数,每层中的节点数以及最佳激活功能。
We can see all results for 40 calls with corresponding hyper-parameters and fitness values.
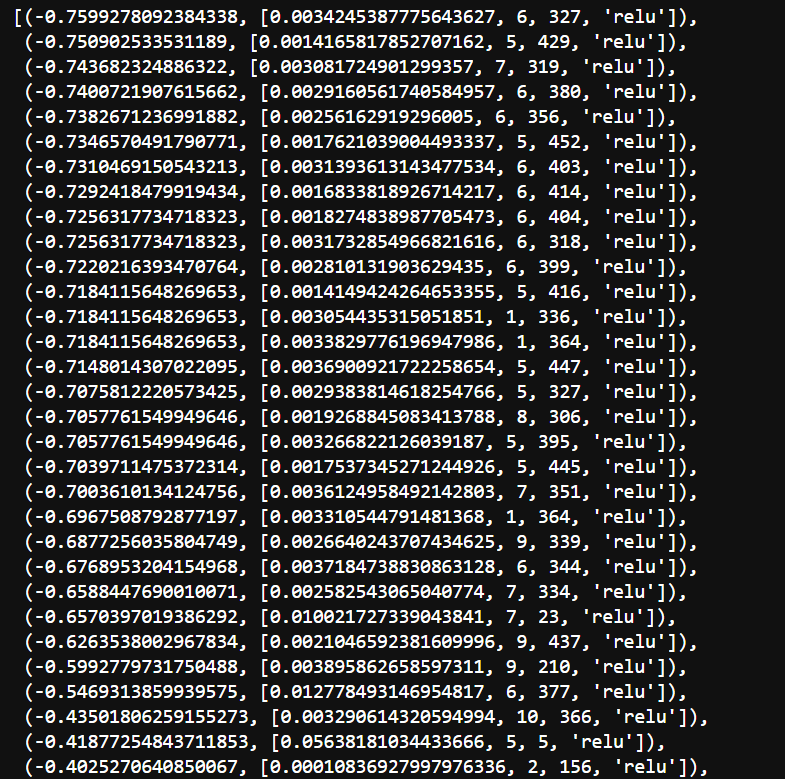
我们可以看到40个带有相应超参数和适用性值的呼叫的所有结果。
sorted(zip(search_result.func_vals, search_result.x_iters))An interesting point is that the ‘relu’ activation function is almost dominant.
有趣的一点是,“ relu”激活功能几乎占主导地位。
情节 (Plots)
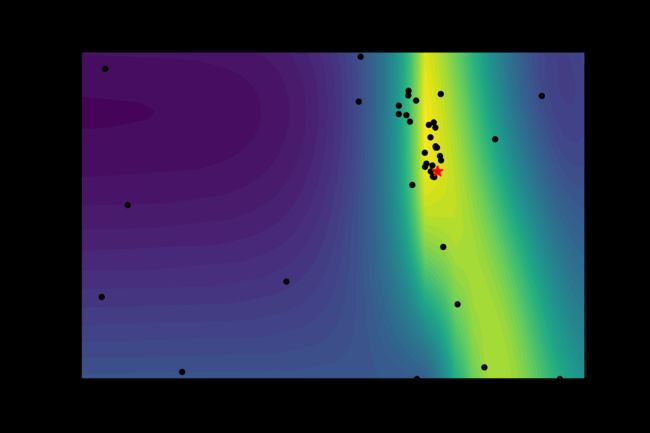
First, let’s look at 2D plot of two optimized parameters. Here we made landscape-plot of estimated fitness values for learning rate and number of nodes in each layer.The Bayesian optimizer builds a surrogate model of search space and searches inside this dimension rather than real search-space, that is why it is faster. In the plot, the yellow regions are better and blue regions are worse. Balck dots are the optimizer’s sampling location and the red star is the best parameter found.
首先,让我们看一下两个优化参数的二维图。 在这里,我们对学习率和每层节点数进行了适合度估计值的景观图。贝叶斯优化器建立了搜索空间的替代模型,并在此维度内进行搜索,而不是在实际搜索空间内进行搜索,这就是为什么它更快的原因。 在该图中,黄色区域较好,蓝色区域较差。 Balck点是优化程序的采样位置,红色星号是找到的最佳参数。
from skopt.plots import plot_objective_2D
fig = plot_objective_2D(result=search_result,
dimension_identifier1='learning_rate',
dimension_identifier2='num_dense_nodes',
levels=50)# plt.savefig("Lr_numnods.png", dpi=400)Some points:
一些要点:
- The surrogate model can be inaccurate because it is built from only 40 samples of calls to the fitness function 替代模型可能不准确,因为它仅由对适应性函数的40个调用样本构建而成
- The plot may change in each time of optimization re-run because of random noise and training process in NN 由于NN中的随机噪声和训练过程,该图可能在每次优化重新运行时都发生变化
- This is 2D plot, while we optimized 4 parameters and could be imagined 4 dimensions. 这是2D图,我们优化了4个参数,可以想象得到4个维度。
# create a list for plotting
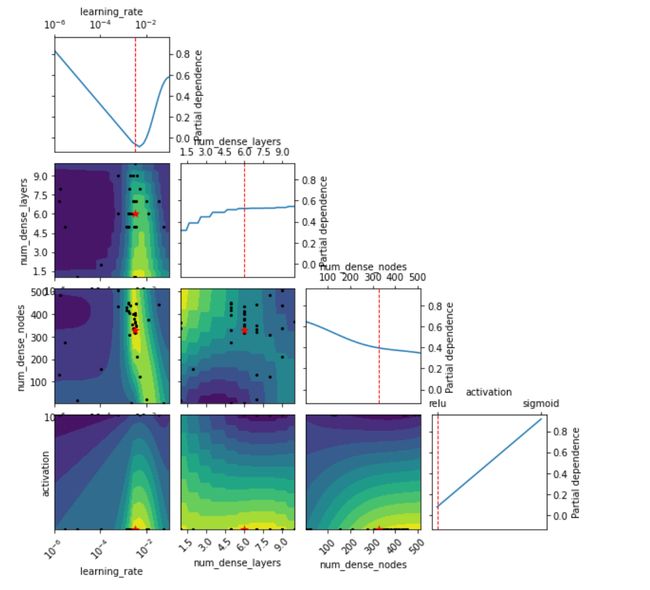
dim_names = ['learning_rate', 'num_dense_layers', 'num_dense_nodes', 'activation' ]fig, ax = plot_objective(result=search_result, dimensions=dim_names)
plt.savefig("all_dimen.png", dpi=400)In these plots, we can see how the optimization happened. The Bayesian approach tries to fit model parameters with prior info at the points with a higher density of sampling. Gathering all four parameters into a scikit-optimization approach will introduce the best results in this run if the learning rate is about 0.003, the number of dense layers 6, the number of nodes in each layer about 327, and activation function is ‘relu’.
在这些图中,我们可以看到优化是如何发生的。 贝叶斯方法试图在具有较高采样密度的点上使模型参数具有先验信息。 如果学习率约为0.003,密集层数为6,每层中的节点数为327,激活函数为“ relu”,则将所有四个参数收集到scikit优化方法中将在此运行中引入最佳结果。 。
使用带有盲数据的优化超参数评估模型 (Evaluate the model with optimized hyper-parameters with blind data)
The same steps of data preparation are required here as well. We skip repeating here. Now we can make a model with optimized parameters to see the prediction.
这里也需要相同的数据准备步骤。 我们在这里跳过重复。 现在我们可以建立一个具有优化参数的模型以查看预测。
opt_par = search_result.x
# use hyper-parameters from optimization
learning_rate = opt_par[0]
num_layers = opt_par[1]
num_nodes = opt_par[2]
activation = opt_par[3]create model:
创建模型:
import numpy as npimport tensorflow.kerasfrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import Dense, Activationfrom tensorflow.keras.callbacks import EarlyStopping
model = Sequential()
model.add(InputLayer(input_shape=(scaled_features.shape[1])))
model.add(Dense(num_nodes, activation=activation, kernel_initializer='random_normal'))
model.add(Dense(labels.shape[1], activation='softmax', kernel_initializer='random_normal'))
optimizer = Adam(lr=learning_rate)
model.compile(optimizer=optimizer, loss='categorical_crossentropy', metrics=['accuracy'])
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3, patience=20,
verbose=1, mode='auto', restore_best_weights=True)
histories = model.fit(X_train,y_train, validation_data=(X_test,y_test),
callbacks=[monitor],verbose=2,epochs=100)let’s see the model accuracy development:
让我们看看模型准确性的发展:
plt.plot(histories.history['accuracy'], 'bo')
plt.plot(histories.history['val_accuracy'],'b' )
plt.title('Training and validation accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.savefig("accu.png", dpi=400)
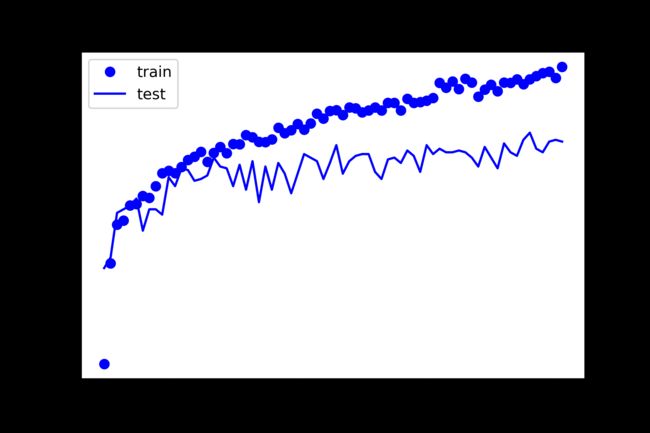
plt.show()Training and validation accuracy plot shows that almost after 80% accuracy (iteration 10), the model starts to overfit because we can not see improvement in test data prediction accuracy.
训练和验证准确性图显示,几乎在80%的准确性(迭代10)之后,该模型就开始过拟合,因为我们看不到测试数据预测准确性的提高。
Let’s evaluate model performance with a dataset that has not seen yet (blind well). We always predict that Machine Learning models will predict with blind data by less accuracy than training process if dataset is small or features are not big enough to cover all complexity of data dimensions.
让我们用一个尚未见过的数据集评估模型性能(很好)。 我们总是预测,如果数据集很小或特征不足以涵盖所有数据维度的复杂性,则机器学习模型将使用盲数据进行预测,其准确性低于训练过程。
result = model.evaluate(scaled_features_blind, labels_blind)
print("{0}: {1:.2%}".format(model.metrics_names[1], result[1]))预测盲井数据和图表 (Predict Blind Well Data and Plot)
y_pred = model.predict(scaled_features_blind) # result is probability arrayy_pred_idx = np.argmax(y_pred, axis=1) + 1# +1 becuase facies starts from 1 not zero like indexblind['Pred_Facies']= y_pred_idxfunction to plot:
绘图功能:
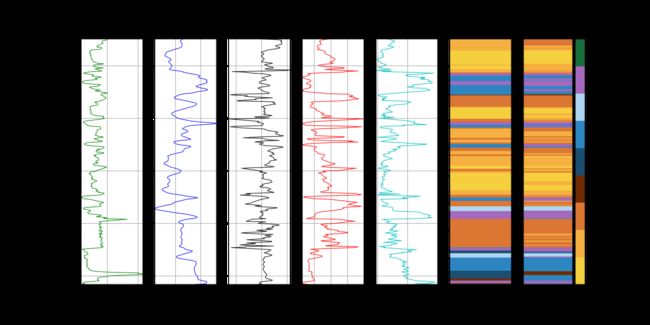
def compare_facies_plot(logs, compadre, facies_colors):
#make sure logs are sorted by depth
logs = logs.sort_values(by='Depth')
cmap_facies = colors.ListedColormap(
facies_colors[0:len(facies_colors)], 'indexed')
ztop=logs.Depth.min(); zbot=logs.Depth.max()
cluster1 = np.repeat(np.expand_dims(logs['Facies'].values,1), 100, 1)
cluster2 = np.repeat(np.expand_dims(logs[compadre].values,1), 100, 1)
f, ax = plt.subplots(nrows=1, ncols=7, figsize=(12, 6))
ax[0].plot(logs.GR, logs.Depth, '-g', alpha=0.8, lw = 0.9)
ax[1].plot(logs.ILD_log10, logs.Depth, '-b', alpha=0.8, lw = 0.9)
ax[2].plot(logs.DeltaPHI, logs.Depth, '-k', alpha=0.8, lw = 0.9)
ax[3].plot(logs.PHIND, logs.Depth, '-r', alpha=0.8, lw = 0.9)
ax[4].plot(logs.PE, logs.Depth, '-c', alpha=0.8, lw = 0.9)
im1 = ax[5].imshow(cluster1, interpolation='none', aspect='auto',
cmap=cmap_facies,vmin=1,vmax=9)
im2 = ax[6].imshow(cluster2, interpolation='none', aspect='auto',
cmap=cmap_facies,vmin=1,vmax=9)
divider = make_axes_locatable(ax[6])
cax = divider.append_axes("right", size="20%", pad=0.05)
cbar=plt.colorbar(im2, cax=cax)
cbar.set_label((5*' ').join([' SS ', 'CSiS', 'FSiS',
'SiSh', ' MS ', ' WS ', ' D ',
' PS ', ' BS ']))
cbar.set_ticks(range(0,1)); cbar.set_ticklabels('')
for i in range(len(ax)-2):
ax[i].set_ylim(ztop,zbot)
ax[i].invert_yaxis()
ax[i].grid()
ax[i].locator_params(axis='x', nbins=3)
ax[0].set_xlabel("GR")
ax[0].set_xlim(logs.GR.min(),logs.GR.max())
ax[1].set_xlabel("ILD_log10")
ax[1].set_xlim(logs.ILD_log10.min(),logs.ILD_log10.max())
ax[2].set_xlabel("DeltaPHI")
ax[2].set_xlim(logs.DeltaPHI.min(),logs.DeltaPHI.max())
ax[3].set_xlabel("PHIND")
ax[3].set_xlim(logs.PHIND.min(),logs.PHIND.max())
ax[4].set_xlabel("PE")
ax[4].set_xlim(logs.PE.min(),logs.PE.max())
ax[5].set_xlabel('Facies')
ax[6].set_xlabel(compadre)
ax[1].set_yticklabels([]); ax[2].set_yticklabels([]); ax[3].set_yticklabels([])
ax[4].set_yticklabels([]); ax[5].set_yticklabels([]); ax[6].set_yticklabels([])
ax[5].set_xticklabels([])
ax[6].set_xticklabels([])
f.suptitle('Well: %s'%logs.iloc[0]['Well Name'], fontsize=14,y=0.94)Run:
跑:
compare_facies_plot(blind, 'Pred_Facies', facies_colors)
plt.savefig("Compo.png", dpi=400)结论 (Conclusion)
In this work, we optimized hyper-parameters using a Bayesian approach with a scikit-learn library called skopt. This approach is superior to a random search and grid search, especially in complex datasets. Using this method, we can get rid of the hand-tuning of hyper-parameters for the neural networks, although in each run, you will face new parameters.
在这项工作中,我们使用贝叶斯方法和一个名为skopt的scikit-learn库优化了超参数。 这种方法优于随机搜索和网格搜索,尤其是在复杂数据集中。 使用这种方法,我们可以摆脱神经网络超参数的手动调整,尽管在每次运行中,您都将面临新的参数。
翻译自: https://towardsdatascience.com/bayesian-hyper-parameter-optimization-neural-networks-tensorflow-facies-prediction-example-f9c48d21f795
贝叶斯优化神经网络参数