【机器学习】逻辑回归案例二：鸢尾花数据分类，决策边界绘制逐步代码讲解

手动反爬虫，禁止转载： 原博地址 https://blog.csdn.net/lys_828/article/details/121929869（CSDN博主：Be_melting）

 知识梳理不易，请尊重劳动成果，文章仅发布在CSDN网站上，在其他网站看到该博文均属于未经作者授权的恶意爬取信息

1 数据加载

导入模块和加载数据

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(color_codes=True)
%matplotlib inline

import warnings
warnings.filterwarnings('ignore')

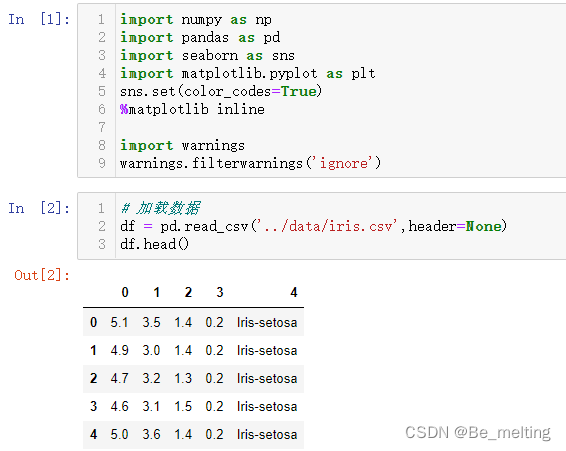
df = pd.read_csv('../data/iris.csv',header=None)
df.head()

输出结果如下。（也可以直接从sklearn中导入dataset数据集，里面包含了鸢尾花数据）

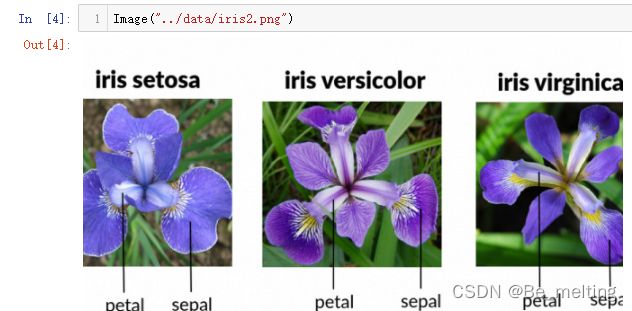
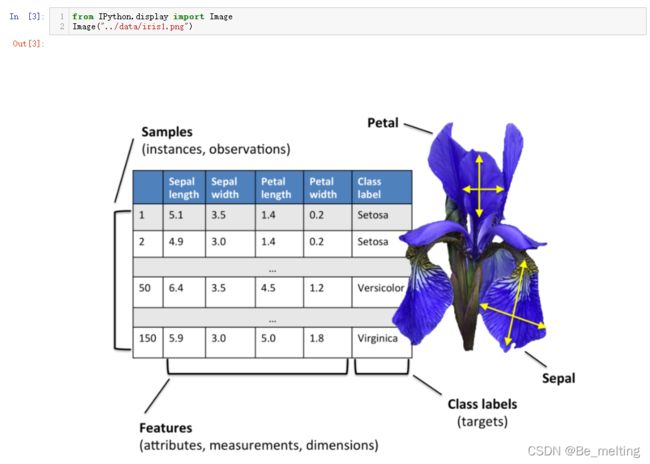
关于iris数据集中的介绍，其中前四个字段就是花萼和花瓣的长和宽，加载图片说明如下。

from IPython.display import Image 
Image("../data/iris1.png")
Image("../data/iris2.png")

输出结果如下。iris数据集一共150条数据，共包含了3类花，各50条数据。对应的四个字段的名称图中也有给出。

对应的三种花的样式，下图中也可以做个直观展示。

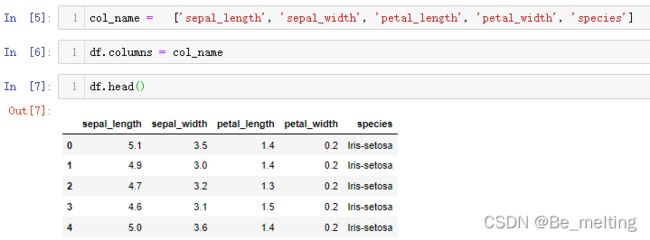
将字段名称修改后指定为读入的数据集，代码如下。

col_name =   ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species']
df.columns = col_name
df.head()

输出结果如下。

2 数据EDA

数据读取后进行探索式分析，首先为了保证原始数据的完整性，尽量在进行分析之前进行数据备份，然后任意选取两个字段进行散点图绘制，查看相关关系。

iris = df.copy()
iris.head()

plt.figure(figsize=(8,8))
sns.scatterplot(data=iris,x='petal_length' ,y='petal_width')

输出结果如下。比如查看花瓣(petal)的长度和宽度之间的关系。

可以借助hue参数，实现分类数据显示，代码如下。

iris.species.unique()
plt.figure(figsize=(5,5))
sns.scatterplot(data=iris,x='petal_length' ,y='petal_width' ,hue='species')

输出结果如下。可以看出不同种类的花瓣的长和宽是有一个较为明显的区分。

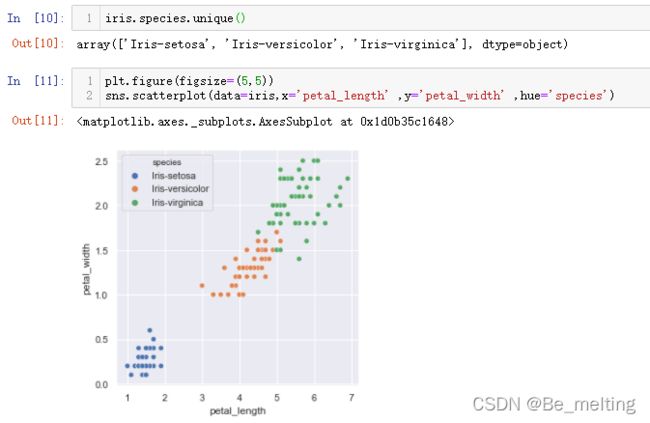
上面两个字段只是随机选择，可能凑巧数据分类的散点图层次较为清晰，更好的方式展现四个字段的关系还是需要使用pairplot绘制，代码如下。

# 通过统计函数 绘制数据点位，核实各种类的数量
print(iris.groupby('species').size())
sns.pairplot(iris,hue='species',size=1.8)

输出结果如下。通过中间对角线的分布图，可以看到每两个字段对应的三种花之间的关联，三条曲线重叠的范围越多，说明彼此之间交叉混合的数据越多，凭借着这两个字段来分别三种花的难度越大。

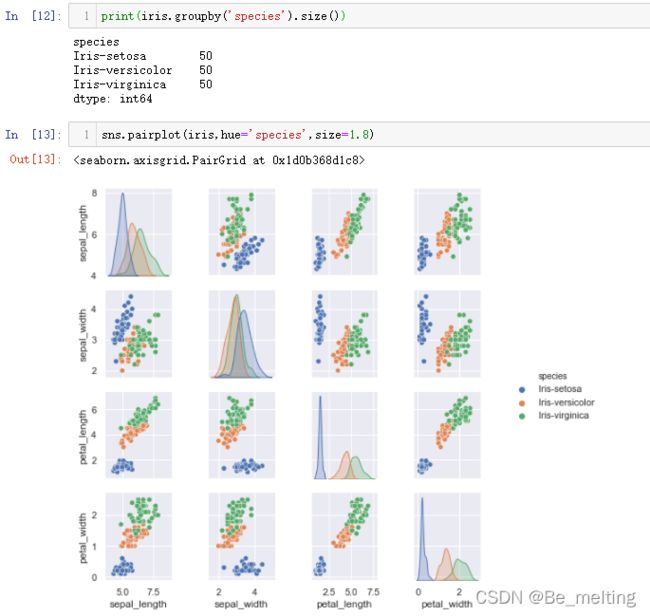
比如单独在探究一下花萼(sepal)长宽与三种花分类之间的关联，绘制分类散点图代码如下。

plt.figure(figsize=(7,7))
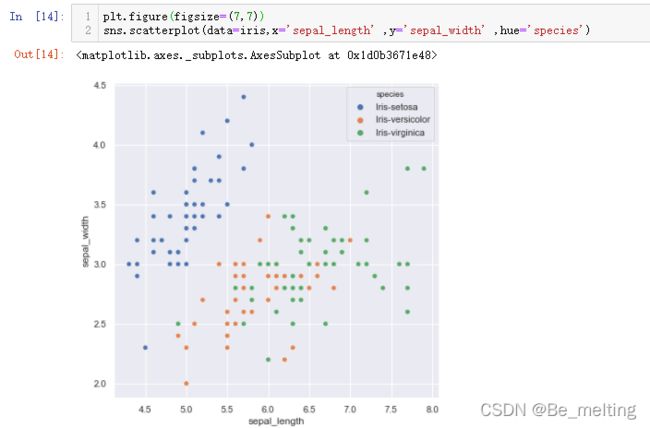
sns.scatterplot(data=iris,x='sepal_length' ,y='sepal_width' ,hue='species')

输出结果如下。可以清晰分辨出iris-setosa和剩下两类花之间的关系，但是剩下的两类花之间的数据彼此交叉，无法直接将其分类清晰，所以如果选择这两个字段进行分类依据最后得到的模型效果也不会太好

3 模型创建及应用

直接通过EDA可以发现，需要通过绘制paiplot图形然后进一步通过人为的选择对应的字段进行三种花的分类，肉眼可能会存在着一定的误差，而直接采用模型来帮忙就能解决这个问题，把所有的字段都给扔进模型，让模型自己学习，最后得到一个最佳结果。

3.1 数据切分

首先要把数据准备好，先处理特征字段和标签字段，代码如下。

features = iris.iloc[:, :-1].values
features.shape
labels = iris.iloc[:, -1].values
labels.shape

输出结果如下。

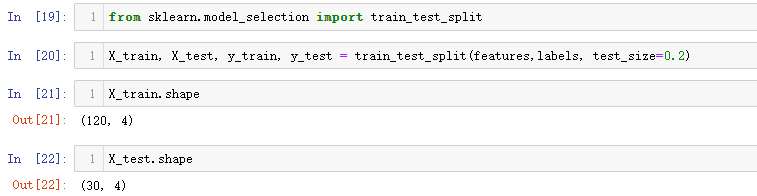
接着就是划分训练集和测试集数据，划分比例为8:2，代码如下。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(features,labels, test_size=0.2)
X_train.shape
X_test.shape

输出结果如下。

3.2 创建模型与分类

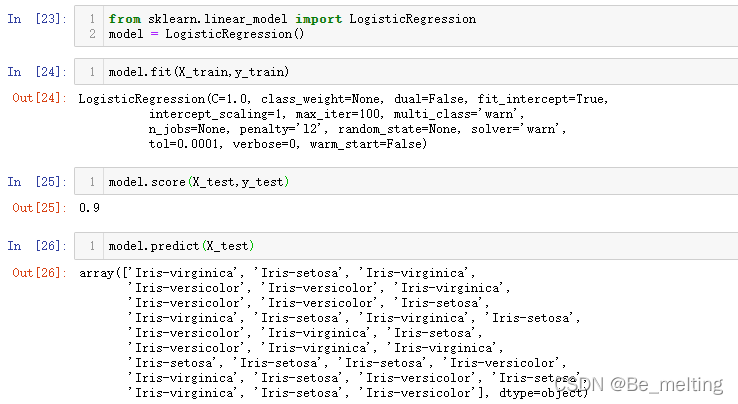
逻辑回归的模型创建和应用的过程要比线性回归多一步，就是进行结果分类，前面的步骤都是一致，代码操作如下。

#第一步：导入模型函数
from sklearn.linear_model import LogisticRegression
#第二步：进行模型初始化
model = LogisticRegression()
#第三步：模型训练
model.fit(X_train,y_train)
#第四步：模型得分/评估
model.score(X_test,y_test)
#第五步：模型预测
model.predict(X_test)

输出结果如下。

以上步骤和线性回归模型分析过程一模一样，至于逻辑回归区别就在于最后的分类上面，需要利用预测的结果，借助混淆矩阵进行可视化展示，代码如下。

y_predicted = model.predict(X_test)
model.intercept_ ,model.coef_

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test,y_predicted)
cm
plt.figure(figsize = (10,7))
sn.heatmap(cm, annot=True)
plt.xlabel('Predicted')
plt.ylabel('Truth')

输出代码如下。逻辑回归是基于线性回归基础上，也可以输出截距和斜率。混淆矩阵的使用很简单，只需要把对应的模块导入后把测试数据和预测数据传入，就自动得到分类的结果，通过热力图可以更加直观地展示。

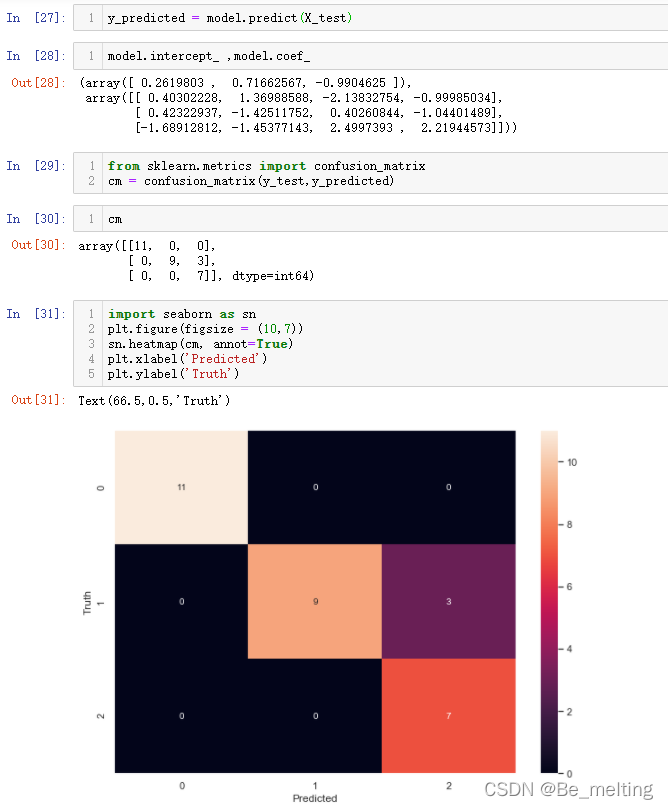
结果解读需要借助一下计数器，由于没有提前进行标签数据的数值化处理，热力图上出来的值并不知道如何对应三种花的信息，因此可以通过预测结果和真实结果的计数比对来确定，代码如下。

from collections import Counter
Counter(list(y_test))

Counter(list(y_predicted))

输出结果如下。热力图中编号为0的是Iris-setosa类别，而热力图中的3个错误分类表示模型把编号1错误分类为编号2，结合着第二行和第三列各自的总和，可以知道编号1是为Iris-versicolor，编号2是Iris-cirginica。

3.3 决策边界绘制

通过上面的一阵分析，可以发现，如果不对标签字段进行字符串编码，最后的输出结果要经过一阵子分析才能知道对应的结果，所以对于字段数据在传入模型时，尽量进行编码处理，比如将三种花的类型进行编码，探究具体数据是如何进行分类。

3.3.1 二分类决策边界绘制

首先查看一下数据，核实标签数据中的分类名称。

iris
iris.species.unique()
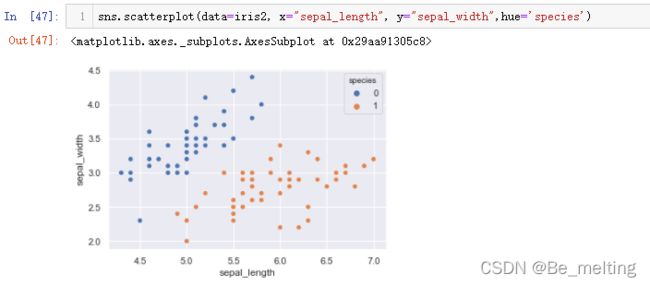
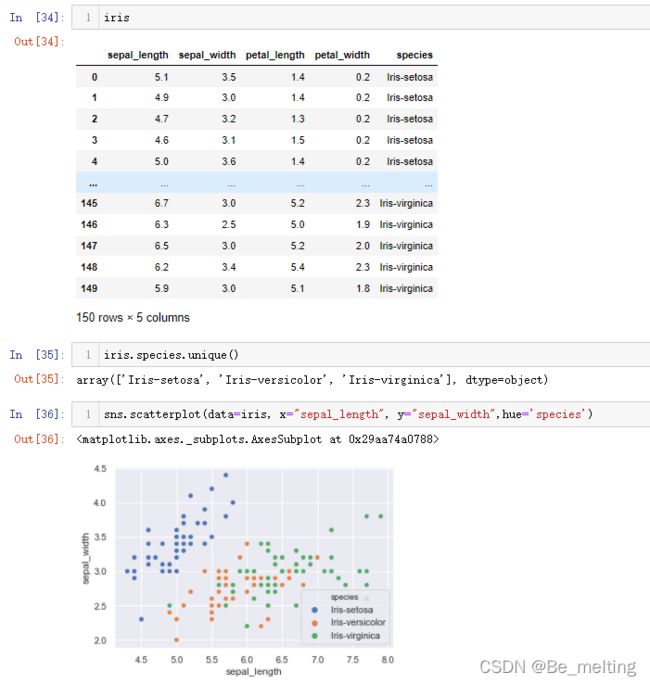
sns.scatterplot(data=iris, x="sepal_length", y="sepal_width",hue='species')

输出结果如下。根据之前按照花萼长和宽绘制的散点图，可以发现三种类别的分类较为复杂，所以为了搞清楚模型是怎么进行分类？可以先取两类数据进行测试。

但是需要把标签字段的编码工作完成，代码操作如下。

def func1(t):
    if t == 'Iris-setosa' :
        return int(0)
    elif t == 'Iris-versicolor':
        return int(1)
    elif t =='Iris-virginica':
        return int(2)
        
iris.head()
iris2 = iris.copy()
iris2.head()
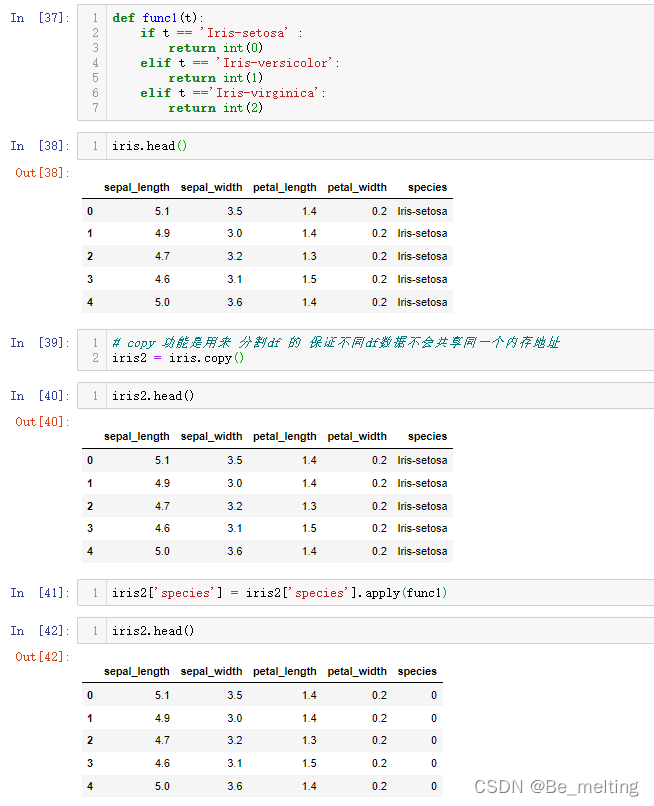
iris2['species'] = iris2['species'].apply(func1)
iris2.head()

输出结果如下。为了防止原始数据被破坏，还是重新进行备份，然后在进行操作。

再次核实下标签字段中的分类名称，并进行某一分类信息的剔除，比如删除第三类数据，代码操作如下。

iris2['species'].unique()
iris2 = iris2[iris2.species != 2]
iris2['species'].unique()
iris2.shape

输出结果如下。

然后对剩下两类花进行散点图绘制，查看具体的数据分布情况，代码如下。

sns.scatterplot(data=iris2, x="sepal_length", y="sepal_width",hue='species')

输出结果如下。

上图中的分类结果是直接利用seaborn中封装的函数进行，接下来第一步要做的就是利用模型来进行分类。还是要执行3.1和3.2中的流程，代码如下。

#数据切分
features2 = iris2.iloc[:, :2].values
labels2 = iris2.iloc[:, -1].values
#模型初始化
model2 = LogisticRegression()
#模型训练
model2.fit(features2,labels2)
#模型评估
model2.score(features2,labels2)

输出结果如下。通过人眼可以直接进行分类的数据，通过模型进行分类，最后的得分也可以高达99%。

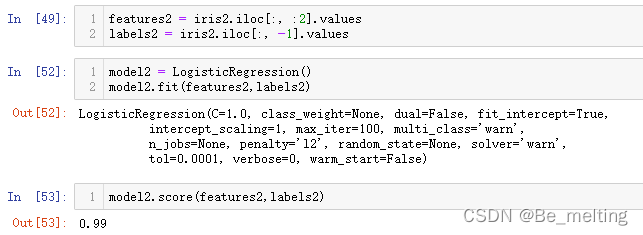
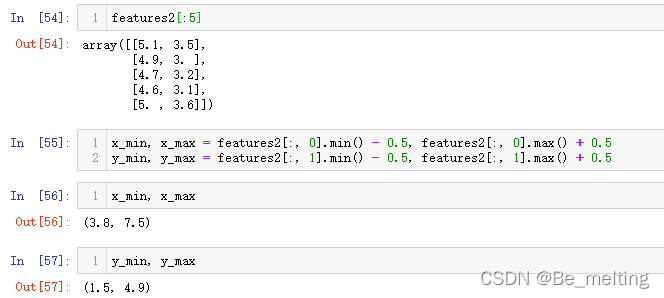
最后就剩下最重要的问题，既然可以实现99%分类正确率，如何进行决策边界的绘制？首先需要获取标签字段中的最小和最大值，代码如下。

features2[:5]
x_min, x_max = features2[:, 0].min() - 0.5, features2[:, 0].max() + 0.5
y_min, y_max = features2[:, 1].min() - 0.5, features2[:, 1].max() + 0.5
x_min, x_max
y_min, y_max

输出结果如下。这里加减0.5是为了后面绘制画布扩大点距离。

通过绘制分类散点图核实一下大致区间无误，同时也可以对比没有进行分类的数据图形，代码及输出如下。图形界面上x和y轴的上下限是在上方索取的范围之间，核实无误。

模型训练好了之后是要进行使用，而绘制决策边界的思想就是在指定的x和y轴指定范围围成的区域内生成很多数据点，然后用模型预测这些数据点，就会形成一个分类的区分，再对两边的数据的进行着色处理就可以得到决策边界。

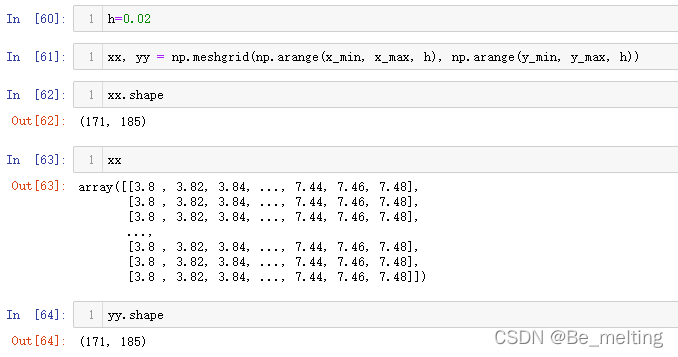
假定按照0.02的距离生成数据点，布满整个区域，可以利用arange()方法，然后结合这meshgrid()就完成了类似棋盘的绘制。可以想象一下五子棋盘的样式，这里构建的数据就是棋盘上的每一个交点的坐标数据，代码如下。

h=0.02
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
xx.shape
yy.shape

输出结果如下。

棋盘绘制完毕后，利用训练好的模型对棋盘中的每一个交点进行预测。但是需要注意，模型预测时候传递的数据类型是二维的数据结构，因此需要把数据给拍扁，结合之前numpy中介绍的ravel()方法就可以实现，代码如下。

xx.ravel()
Z = model2.predict(np.c_[xx.ravel(), yy.ravel()])
Z

输出结果如下。

自此模型就把网盘上的交点都预测出对应的结果，剩下的就是进行绘制图形，具体需要使用到pcolormesh()方法，测试使用代码如下。

Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(6, 6))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)

输出结果如下。这里有一个留意的地方，预测出来的结果是一个一维数据结果，要在图形x和y轴上显示就必须转化为原来的数据形状大小，直接进行reshape()即可。

使用pcolormesh()方法绘制图像就和使用散点图绘制的方式类似，都是把对应的数据传入，不过这里是根据x和y轴的信息，将预测的z值绘制出来。再添加上二分类的数据，代码如下。

plt.figure(1, figsize=(6, 6))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
plt.scatter(features2[:, 0], features2[:, 1], c=labels2, edgecolors="k", cmap=plt.cm.Paired)
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")

plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())

输出结果如下。图中分割线处锯齿形状就是说明这个图形是由一个个点组成。

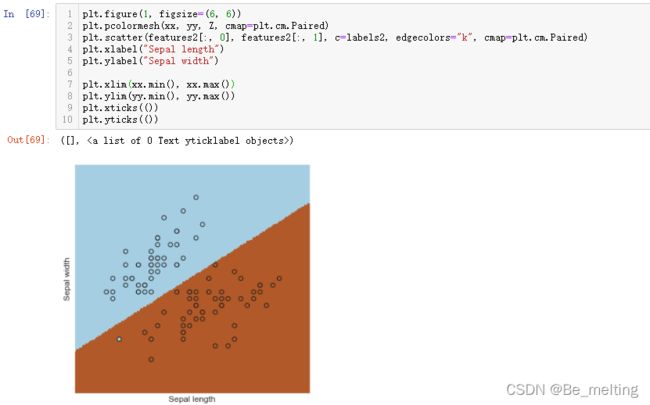
对比一下使用seaborn中hue参数进行绘制的分类图，代码及输出结果如下。

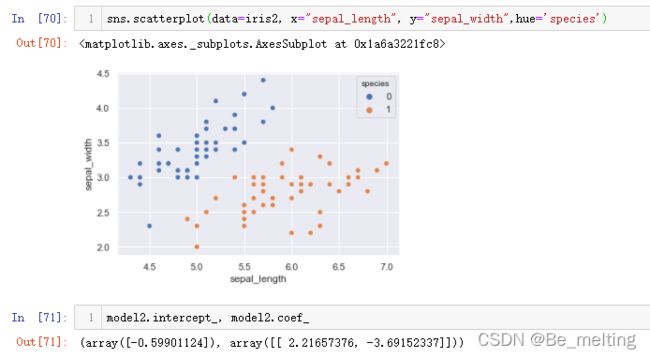
然后也可以输出最终决策边界的截距和斜率，至此二分类决策边界的绘制就介绍完毕。

3.3.2 多分类决策边界绘制

依旧重新备份一下数据，将标签数据进行编码处理，然后再通过seaborn中的分类散点图快速查看数据分布，代码如下。

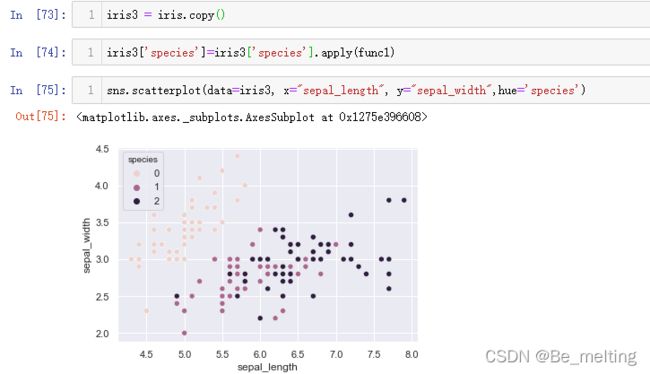
iris3 = iris.copy()
iris3['species']=iris3['species'].apply(func1)
sns.scatterplot(data=iris3, x="sepal_length", y="sepal_width",hue='species')

输出结果如下。

接着进行数据集切分和模型创建及预测的操作，代码如下。

iris3.head()
features3 = iris3.iloc[:, :2].values
labels3 = iris3.iloc[:, -1].values

model3 = LogisticRegression()
model3.fit(features3,labels3)
model3.score(features3,labels3)

输出结果如下。此次模型的分类预测得分明显降了下来，只达到了76.7%。

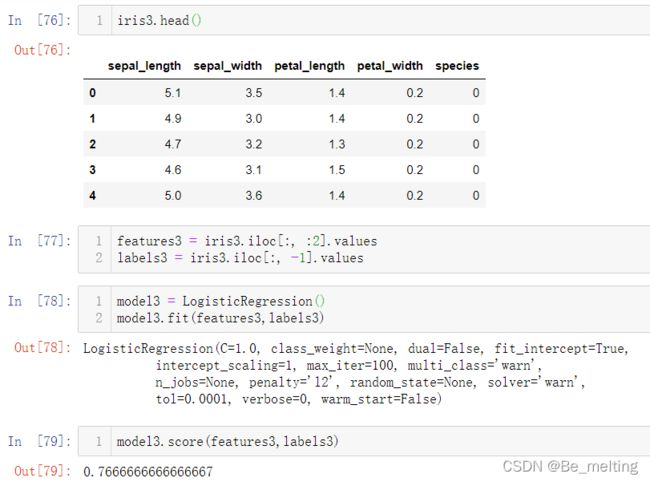
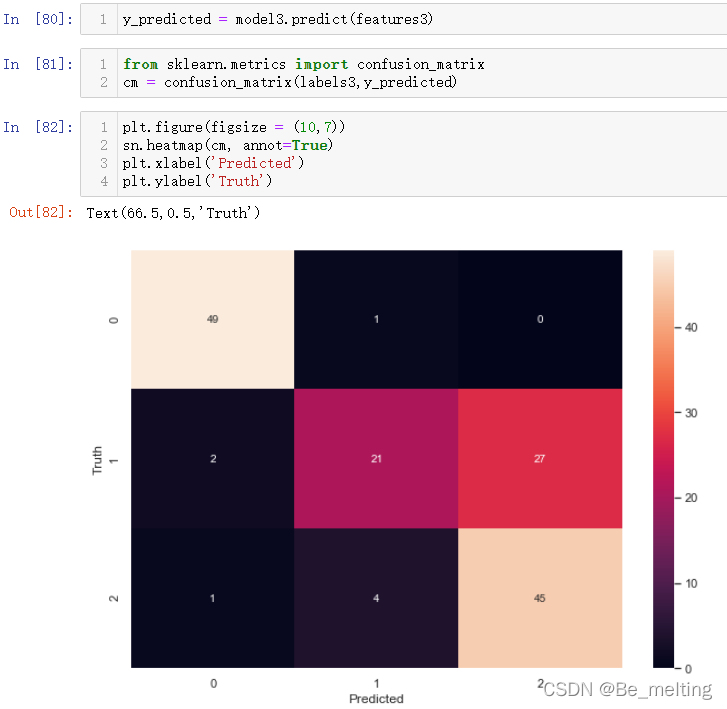
通过混淆矩阵来看一下分类的结果，代码如下。

y_predicted = model3.predict(features3)

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(labels3,y_predicted)

plt.figure(figsize = (10,7))
sn.heatmap(cm, annot=True)
plt.xlabel('Predicted')
plt.ylabel('Truth')

输出结果如下。这里的过程和之前的一致，最主要的就是进行了标签字段数据的编码这里的0,1,2可以一一对应上，不需要再进行计数分析了。

在可视化的热图上也可以清晰看出编号1类花和编号2类的花之间确实难以进行划分，按照二分类决策边界绘制的思路，应用到当前数据中，流程一模一样，代码如下。

#指定x和y轴取值范围
x_min, x_max = features3[:, 0].min() - 0.5, features3[:, 0].max() + 0.5
y_min, y_max = features3[:, 1].min() - 0.5, features3[:, 1].max() + 0.5
#绘制棋盘
h = 0.02  
plt.figure(figsize=(8,8))
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
#对棋盘中的每一个交点进行分类预测
Z = model3.predict(np.c_[xx.ravel(), yy.ravel()])
#把预测的结果展现在二维图像上，绘制决策边界
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
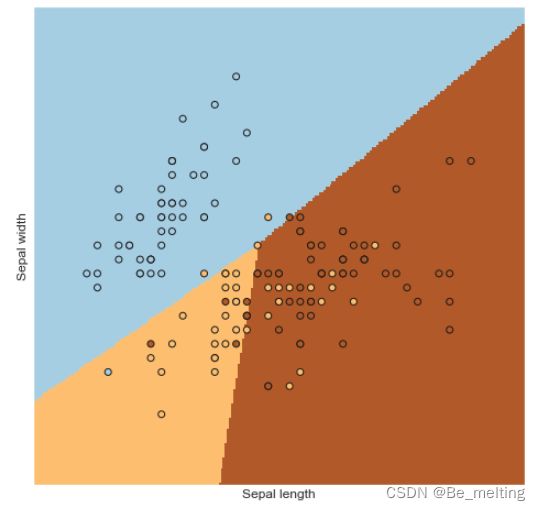
#添加原始数据
plt.scatter(features3[:, 0], features3[:, 1], c=labels3, edgecolors="k", cmap=plt.cm.Paired)
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
#坐标刻度和取值范围设置
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
#显示图像
plt.show()

输出结果如下。图像中的分界线的锯齿状也说明决策边界是有一个个点构成。

至此多分类决策边界的绘制就介绍完毕。此处留有一个问题：如果不使用前两个字段进行绘制，而是选择其他的两个字段，输出结果如何呢？在进行特征字段选取的时候将列数进行改变即可，比如[0,2],[0,3],[1,2],[1,3],[2,3]还有5种情况没有进行测试

features3 = iris3.iloc[:, :2].values
features4 = iris4.iloc[:, [0,2]].values
features5 = iris5.iloc[:, [0,3]].values
features6 = iris6.iloc[:, [1,2]].values
features7 = iris7.iloc[:, [1,3]].values
features8 = iris8.iloc[:, [2,3]].values

可能有个疑问：这里为啥只选两个字段？就是因为这里的决策边界是二维的，只能通过两个字段才能绘制出来直线，如果三个字段就是下面的三维决策平面的绘制。同理下面三维决策平面的绘制也面临同样的情况，就是选哪三个字段进行呈现，4个字段选择3个一共有4种选择方式。

3.3.3 三维决策平面的绘制

仅做了解，全部代码如下。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from mpl_toolkits.mplot3d import Axes3D

iris = datasets.load_iris()
X = iris.data[:, :3]  # we only take the first three features.
Y = iris.target

#make it binary classification problem
X = X[np.logical_or(Y==0,Y==1)]
Y = Y[np.logical_or(Y==0,Y==1)]

model = LogisticRegression()
clf = model.fit(X, Y)

# The equation of the separating plane is given by all x so that np.dot(svc.coef_[0], x) + b = 0.
# Solve for w3 (z)
z = lambda x,y: (-clf.intercept_[0]-clf.coef_[0][0]*x -clf.coef_[0][1]*y) / clf.coef_[0][2]

tmp = np.linspace(-5,5,30)
x,y = np.meshgrid(tmp,tmp)

fig = plt.figure()
ax  = fig.add_subplot(111, projection='3d')
ax.plot3D(X[Y==0,0], X[Y==0,1], X[Y==0,2],'ob')
ax.plot3D(X[Y==1,0], X[Y==1,1], X[Y==1,2],'sr')
ax.plot_surface(x, y, z(x,y))
ax.view_init(30, 60)
plt.show()

输出结果如下。

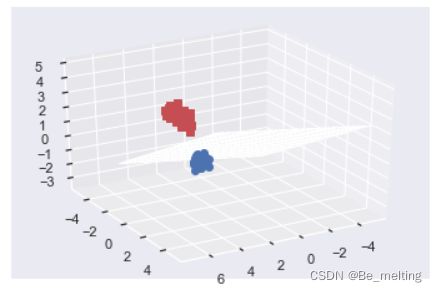
最后就是这种二维或者三维的决策边界都是只选取了原特征数据中的部分字段，无论怎么进行模型的分类最后的模型得分始终超不过使用全部字段训练的模型的结果，也就是最开始的模型model.score()输出的结果：0.967。但是这种二维或者三维的决策边界的绘制是有意义的，后续的实战案例中的数据字段会有很多，但是并不是每一个字段都是对结果有着影响，因此就可以进行降维的方式将有效的信息进行提取，数据的维度降低后，就可以再进行决策边界的展示。