基于python的线性代数运算
前言:这是学校多元统计分析课程布置的实验(包括基于python的线性代数运算、线性回归分析实验、聚类分析、因子分析和主成分分析),这里分享出来,注解标注的比较全,供大家参考。
使用Python语言开发完成以下运算。
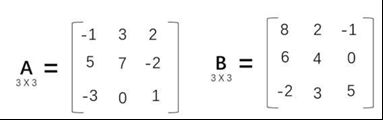
1、已知有两个矩阵A和B,如下所示:
①求A+B、A-B;
import numpy as np
import pandas as pd
from fractions import Fraction
# 这里定义一个单位矩阵,作为结果判断依据
temp = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
# 定义矩阵A
A = np.array([[-1, 3, 2],
[5, 7, -2],
[-3, 0, 1]])
# 定义矩阵B
B = np.array([[8, 2, -1],
[6, 4, 0],
[-2, 3, 5]])
# A+B
print(A+B)
# A-B
print(A-B)
②求A和B的叉乘、A和B的点乘;
# 两个矩阵的叉乘
AXB = np.cross(A, B)
print(AXB)
# 两个矩阵的点乘
AB = np.dot(A, B)
print(AB)
③令C=A*B,求C的逆矩阵、行列式;
# np.linalg.inv求矩阵的逆矩阵
C = np.linalg.inv(AB)
# np.linalg.det求矩阵的行列式
CH = np.linalg.det(AB)
④验证C和C的逆矩阵之积是否为单位矩阵;
print(np.array(C.dot(AB), dtype=int))
2、读取文件“test1-2.csv”,获取25*4的矩阵D:
①求矩阵D的转置矩阵G;
# 设置矩阵元素输出用分数表示
np.set_printoptions(formatter={'all': lambda x: str(Fraction(x).limit_denominator())})
# 这里如果不设置header=None默认就将数据第一行当作数据头
df = pd.read_csv("test1-2.csv", header=None)
# 转置矩阵
G = np.mat(df.T)
②求矩阵G的相关系数矩阵(4*4)E;
# 平均值
mean = df.mean()
# 标准差
std = df.std()
# 协方差
F = np.mat(df.cov())
# 相关系数
# E = np.mat(F/np.mat(std))
E = np.corrcoef(G)
③求矩阵G的协方差矩阵(4*4)F;
# 协方差
F = np.mat(df.cov())
④求解矩阵E和矩阵F的特征值和特征向量;
# 矩阵E的特征值a,特征向量b
a, b = np.linalg.eig(E)
# 矩阵F同理
⑤验证矩阵E的特征向量间的正交性;
'''
验证矩阵E的特征向量间的正交性
https://www.cnpython.com/qa/139953
'''
print(b.dot(b.T))
⑥验证矩阵E的特征值之和是否等于E的迹;
# 矩阵E的迹
traceE = np.trace(E)
# 矩阵E的特征值a
a, b = np.linalg.eig(E)
# 矩阵E的特征值之和sumE
sumE = round(sum(a), 8)
print(sumE == traceE)
⑦对矩阵D的做奇异值分解,输出左奇异矩阵、奇异值和右奇异矩阵,并查看左奇异矩阵和右奇异矩阵是否为正交矩阵;
'''
对矩阵D的做奇异值分解,输出左奇异矩阵、奇异值和右奇异矩阵,并查看左奇异矩阵和右奇异矩阵是否为正交矩阵。
https://jingyan.baidu.com/article/e75057f2385f34ebc81a8944.html
'''
# u - ;v - 奇异值;w -
u, v, w = np.linalg.svd(df)
print(u)
# 左奇异矩阵
print(u)
# 奇异值
print(v)
# 右奇异矩阵
print(w)
# 将v转化为对角矩阵
v = np.diag(v)
print(u)
# 查看左奇异矩阵和右奇异矩阵是否为正交矩阵。
u = u.dot(u.T)
w = w.dot(w.T)
print(u)
'''
将矩阵与单位矩阵比较np.allclose(w, np.eye(4))
np.eye()中的参数按照生成的矩阵的格式
https://www.cnpython.com/qa/164423
'''
print(np.allclose(u, np.eye(25)))
print(np.allclose(w, np.eye(4)))
tips:
q1:在验证一个矩阵和其逆矩阵相乘时是否等于单位矩阵,发现结果包含许多接近于0但不等于0的科学计数法的数字。
a1:网上说因为矩阵接近奇异值,也就是在我们求其逆矩阵时会出现伪逆,或者无穷小数,那么我们在求逆矩阵时就不要使用pinv求逆矩阵,因为此方法会把矩阵的伪逆求出来如果逆不存在的话,第二就是输出结果转换为int类型,去掉小数即可。
q2:进行验证矩阵E的特征值之和是否等于E的迹时,发现矩阵E的特征值之和不为期望结果。
a2:从输出的特征值可以看出所有数值都是8位小数,所以在使用函数计算时可能有小数的四舍五入。那么他们之间的和有出入是必然的,但是结果的误差非常小,所以只需对结果取整即可。
实验所用到的所有文件获取1
实验所用到的所有文件获取2,提取码:uj7m