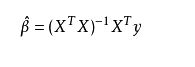一文带你解决python线性代数矩阵运算
想必大家都学习过线性代数这门课程,也被其中的矩阵运算弄得茶饭不思,苦不堪言,今天就带着大家用python解决矩阵运算的大难题!!!
一,矩阵的创建
在python中,numpy是一个非常强大的包,我们通常使用它来解决矩阵的相关问题,使用numpy创建矩阵有以下几种方法
首先是导入numpy包,这是我们开始的基础,不要忘记了。
import numpy as np
1.使用numpy库的matrix直接创建

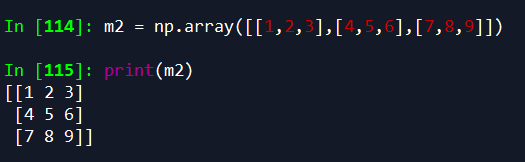
2.使用numpy库的array来创建矩阵
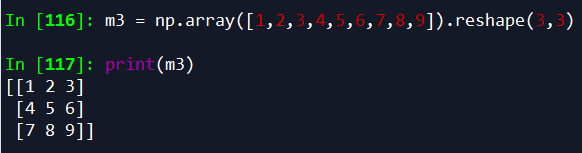
3.使用reshape()来改变数组的形状
二,特殊矩阵的创建
刚刚介绍了一般矩阵的创建方法,可是我们有时候会用到一些特殊的矩阵,下面将给大家
介绍一些特殊矩阵的创建方法,一起来看看吧!
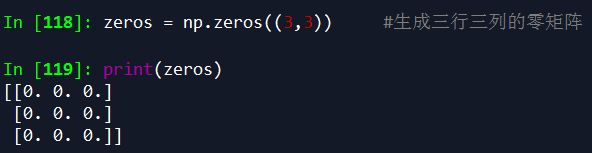
1.使用np.zeros()可以生成全是0的矩阵
2.使用np.ones可以生成全是1的矩阵

3.使用np.identity可以生成单位矩阵

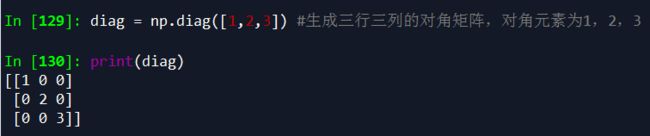
4.使用np.diag可以生成对角矩阵
三.numpy中的random随机函数的使用
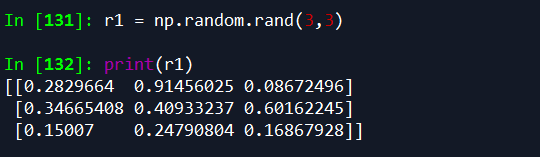
1. np.random.rand(d0,d1,…,dn)
根据给定维度生成[0,1)之间的数据,这些数据包含0,不包含1,其中dn表示每个维度,返回值为指定维度的array。
2. numpy.random.randn(d0,d1,…,dn)
randn函数返回一个或一组样本,具有标准正态分布。dn表示每个维度,返回值为指定维度的array。

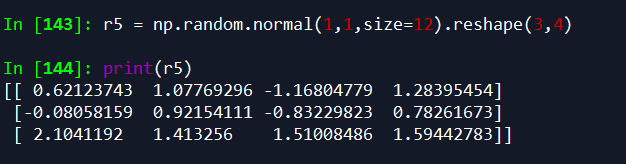
3. np.random.normal(loc=0.0, scale=1.0, size=None)
生成一个均值为loc(float),方差为scale(float)的服从高斯分布的概率密度随机数。


生成服从正态分布随机数的矩阵
四.矩阵的运算
前面讲了那么多矩阵的知识,就是为下面解决矩阵运算做的准备。让我们一起来解决吧!!!
1.矩阵的加减法
首先生成两个矩阵

矩阵加法和传统上的加法一样,对应位置相加。

矩阵减法也是一样的操作

2.矩阵乘法
还是使用上面创建的两个矩阵m1和m2,下面我用三种方法来实现两个矩阵相乘



3.矩阵转置
还是使用上面创建的两个矩阵m1和m2。矩阵转置也有三种方法。
第一个是 .T 的方法
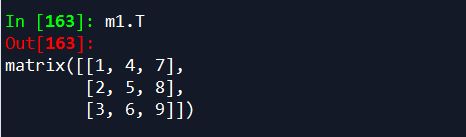
第二个和第三个原理一样


4.矩阵求逆
使用前面的m1矩阵 m1 = np.matrix([[1,2,3],[4,5,6],[7,8,9]])
第一种是用 .I 的方法
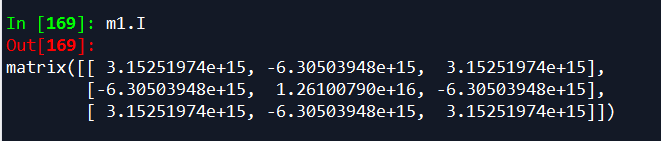
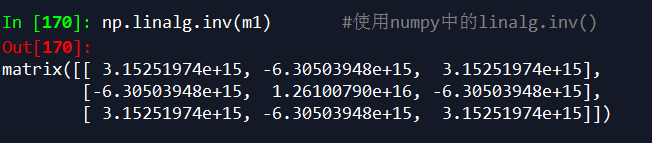
第二种是使用numpy中的linalg.inv() 方法
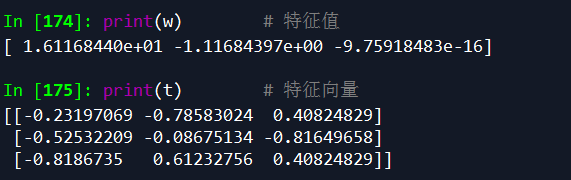
5.矩阵求特征值和特征向量 np.linalg.eig()
求 m1 = np.matrix([[1,2,3],[4,5,6],[7,8,9]]) 的特征值和特征向量

6.矩阵的迹。即对角线元素之和

7.求行列式的值 np.linalg.det()
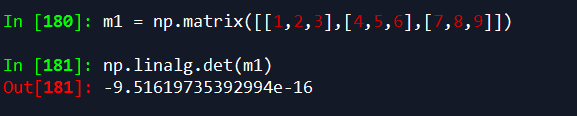
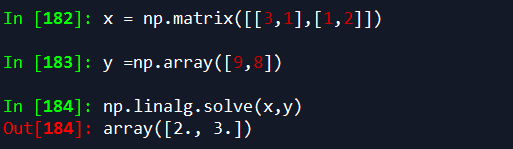
8.矩阵形式的线性方程的解 np.linalg.solve(x,y)
解方程组: 3 * x0 + x1 = 9 , x0 + 2 * x1 = 8
五.学以致用
求解多元回归方程参数的最小二乘估计
忘记理论推导的可以看这里 https://baike.baidu.com/item/最小二乘法/2522346?fr=aladdin
首先给出两个矩阵X,Y,其中X是10行3列的矩阵,Y是10行1列的矩阵。