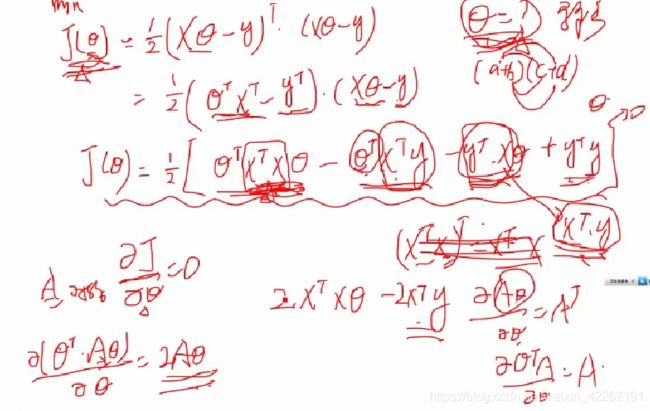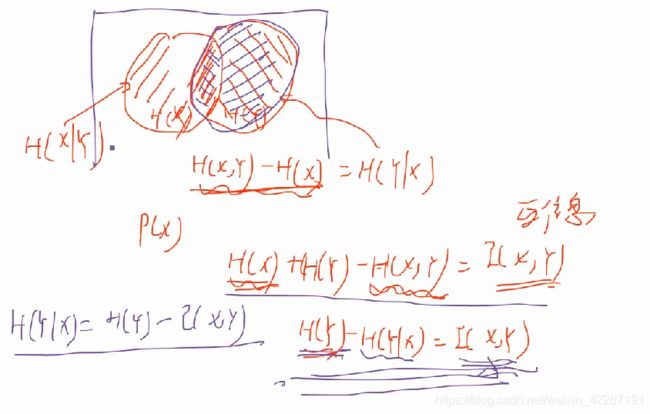机器学习相关笔记__数学知识扩展(内容杂且多，部分总结较浅)

数学知识扩展

期望和方差

期望

在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

方差

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。

方差是实际值与期望值之差平方的平均值，而标准差是方差算术平方根。 在实际计算中，我们用以下公式计算方差。

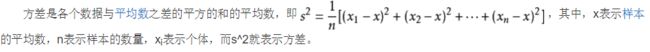
方差是实际值与期望值之差平方的平均值，而标准差是方差算术平方根。 在实际计算中，我们用以下公式计算方差。

协方差

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

x和y事件不相关,则协方 差为0

大于0趋势相同

<0趋势相反

协方差其意义：

度量各个维度偏离其均值的程度。协方差的值如果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)，结果为负值就说明负相关的，如果为0，也是就是统计上说的“相互独立”。

当 cov(X, Y)>0时，表明 X与Y 正相关；

当 cov(X, Y)<0时，表明X与Y负相关；

当 cov(X, Y)=0时，表明X与Y不相关。

对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

标准差:

方差开平方

协方差矩阵:

最大似然估计:

2.矩阵和线性代数

矩阵:m*n 方阵:n *n

正交阵:

A.T A=I

奇异阵：

首先，看这个矩阵是不是方阵（即行数和列数相等的矩阵。若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵）。 然后，再看此矩阵的行列式|A|是否等于0，若等于0，称矩阵A为奇异矩阵；若不等于0，称矩阵A为非奇异矩阵。 同时，由|A|≠0可知矩阵A可逆，这样可以得出另外一个重要结论:可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。　如果A为奇异矩阵，则AX=0有无穷解，AX=b有无穷解或者无解。如果A为非奇异矩阵，则AX=0有且只有唯一零解，AX=b有唯一解。

单位正交阵:

A.T A=I 且IAI=I

SVD分解(奇异值分解):

eg:应用,图像的虚化,将图片像素矩阵做svd处理,处理后奇异值矩阵取排在前面的若干个值,取的值越少图像越虚化.

代数余子式:

是一个数值,不是矩阵

---

伴随矩阵:

方阵的逆:

范德蒙行列式:

矩阵和向量的乘法:

向量秩和方程组:

特征值和特征向量：

正定阵：

就是正数在矩阵的推广

对向量求导

QR分解(可以用来求特征值)

通过不断的迭代，最后可以求得特征值

3.回归

1)首先对数据进行分析，有些数据对结果没有强相关性，要筛选出去，方法可以用包含该数据时的整体数据的均方差值和不加该数据的均方差值来判断。

2).岭回归和lasso回归与线性回归的对比。

岭回归L2范数正则化与Lasso回归L1正则化的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的，这两种回归均通过在损失函数中引入正则化项来达到目的

使用解析解A.T A必须是可逆的。因为A.T A是半正定的，所以如果不可逆，加一个小扰动可以继续用上式求最优解。

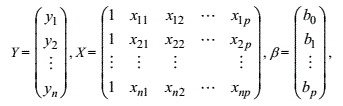
1、若矩阵A的秩r(A)=m，①当n=m，则行向量，列向量均线性无关②当n＞m，行向量线性无关，列向量线性相关。

2、若矩阵A的秩r(A)=n，①当m=n，则行向量，列向量均线性无关②当m＞n，列向量线性无关，行向量线性相关。

矩阵的逆(伪逆)，方阵的逆：

线性回归（注意）

用梯度下降方法求线性回归问题最终得到的一定是最优解而不会有局部最优解的问题。因为其求导时的损失函数是一个二次方的凸函数，二次方凸函数只有一个最优解。

注意***************

所谓线性回归是对参数的线性回归，预设的函数可以是多阶的，如：

y=mx1+b

y=m1x1^2+m2x1+b

事实x1^2是可以通过x1提供的数据事先算出来的，所以最后还是转化为一个关于参数的线性函数

对矩阵的几个求导公式

logistic回归（逻辑回归）

利用sigmod函数，被广泛用于分类问题。

**注意：**逻辑回归是没有上述解析解的，只能通多梯度下降来求。

批量梯度下降和随机梯度下降

随机梯度下降（mini_batch）和批量梯度下降（batch）相比速度更快，可能会跳过局部最优解，而且可以在线做优化不需要等数据全部收集全。随机梯度下降实际中用的可能更多

逻辑回归和线性回归的损失函数是不一样的。

逻辑回归是通过最大似然函数来进行推导的梯度下降公式，线性回归是用均方差公式推导的梯度下降公式。

逻辑回归若遇到多分类问题，将每种情况单独计算再用softmax函数进行分类

softmax回归

用在多分类问题

分类器：

SVM、Logistics，CART

4.决策树和随机森林

决策树可以做分类（y是离散的）也可以做回归（y是连续的）。核心问题是一个节点如何划分（熵降低的程度更快），何时不需要划分了（熵为0了或者样本个数小于一个阈值）。

交叉熵：

交叉熵为逻辑回归的损失函数

熵和联合熵：

信息的混乱不确定程度。

信息熵和信息增益

信息增益即是表示特征X使得类Y的不确定性减少的程度。（分类后的专一性，希望分类后的结果是同类在一起）

信息增益越大，熵的变化程度越大，分的越干脆，越彻底。不确定性越小。

在构建决策树的时候就是选择信息增益最大的属性作为分裂条件（ID3），使得在每个非叶子节点上进行测试时，都能获得最大的类别分类增益，使分类后数据集的熵最小，这样的处理方法使得树的平均深度较小，从而有效提高了分类效率。

信息增益：ID3

g（D,Y）= H(X) - H(X|Y)

信息增益率：C4.5

问题在于行编号的分类数目太多了，分类太多意味着这个特征本身的熵大，大到都快是整个H(X)了为了避免这种现象的发生，我们不是用信息增益本身，而是用信息增益除以这个特征本身的熵值，看除之后的值有多大！这就是信息增益率.

g（D,Y）/ H(Y)

Gini系数：CART

二分类问题时，基尼系数=2p（1-p）

剪植

预剪枝和后剪枝

预剪枝：边建立决策树边进行剪枝的操作（更实用）

后剪枝：当建立完决策树后来进行剪枝操作

bagging

随机森林(防止决策树过拟合)

类似深度神经网络中的dorpout，，随机丢掉一些特征之后最后做整合，可以防止过拟合

5.svm

分类器，泛化能力比逻辑回归要好

求点到线的距离公式如上，如果w已经做过归一化，则直接将各种点带进去可以算出最小的距离。

最上面公式的解释:每个w和b值组成的直线方程将点带进去算这些点中当前距离该直线的最小距离，遍历每个w和b算出的最小距离中的最大值对应的w，b值为最好的分割线。

sign：正的话为1，负的话为-1。

6.k-means

降维<=>聚类<=>无监督学习

k均值算法，不断取均值将数据划分开，无监督学习。但是对初始值比较敏感，比如是二分还是3分4分，如何定。

一般初始值的选取用渐进的方式，比如4分类，先选一个初值计算所有点距离该中心的距离，然后用距离作为权重选择下一个初始点，再计算距离分类，然后再选点。。。。

7.EM算法

无监督分类：k-means EM

高斯混合模型GMM