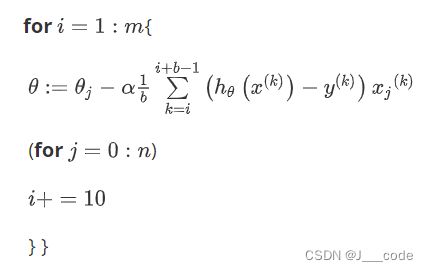吴恩达机器学习课程-第十周

1.大规模机器学习

1.1 大型数据集的学习

在线性回归模型中，如果使用的数据集样本数很大，由于每进行一次梯度下降都需要计算整个训练集的误差的平方和，这需要较大的计算量。所以首先应该做去检查要训练出一个较好的模型是否需要大数据集，可以绘制学习曲线来帮助判断。从左子图中较大的$J_{cv}(\theta )$的值可以看出该模型是一个高方差的模型(即过拟合)，所以增加训练样本可以提升模型效果；从右子图中较大的$J_{train}(\theta )$的可以看出模型是一个高偏差的模型(即欠拟合)，所以增加训练样本无法提升模型效果

1.2 随机梯度下降法(Stochastic Gradient Descent)

考虑训练集所有样本数的梯度下降法称为批量梯度下降，如果采用该方法时数据量过大会导致计算成本过高(比如需要一次将所有数据加载到内存中)。如果需要大规模的训练集，可以尝试使用随机梯度下降法(SGD)来代替批量梯度下降法

SGD中定义代价函数为对单一训练实例的代价，即$cost(\theta )=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}){)}^2,J(\theta )=\frac{1}{m}{\sum }_{i=1}^{m}cost(\theta )$。对于的梯度下降过程为：

1. 随机打乱训练集
2. 遍历所有的训练集样本$i$，更新每一个特征$j$，即$\theta :={\theta }_j-\alpha (h_{\theta }(x^{(i)}-y^{(i)}))x_j^{(i)}$

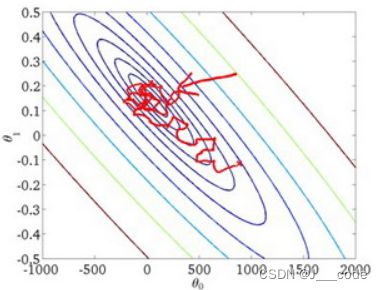
SGD每次针对一个样本更新梯度相当于对单个样本进行拟合，这就可能导致不一定每一次更新都是朝向正确的方向移动。如下图所示，梯度会朝向最小值方向，并且更新的速度很快(遍历一个样本就移动一次)，但是最后一直在最小值附近徘徊(批量梯度下降会走到最小值的位置)，但实际上梯度最终接近最小值即可：

1.3 小批量梯度下降(Mini-Batch Gradient Descent)

小批量梯度下降即介于批量梯度下降和SGD之间的算法，每次计算$b\in (1,m)$个训练实例就更新一次参数，过程如下所示：

​相较于批量梯度下降优势依旧是梯度更新速度快，不需要一次将所有数据加载到内存中；相较于SGD的优势在于可以并行计算梯度。该方式的缺点在于需要确定$b$值的大小

1.4 随机梯度下降收敛

在批量梯度下降中可以根据画出$J(\theta )$和$iter$的关系图来判断梯度下降是否收敛。但是在大规模的训练集的情况下，要进行多次迭代训练计算代价太大。而在SGD中每次采用样本$(x^{(i)},y^{(i)})$更新梯度前都计算一次代价$cost(\theta ,(x^{(i)},y^{(i)})$，每训练$k$个样本就计算这些样本代价的平均值，然后画出均值与每次迭代(经过$k$个样本算一次迭代)的次数之间的函数图表

​假设随着迭代次数的增加，代价均值在不断上升，此时可以考虑将学习率随着迭代次数的增加而减小，比如$\alpha =\frac{const1}{iterNum+const2}$，这样就迫使算法收敛而不是在最小值附近震荡

2.参考

https://www.bilibili.com/video/BV164411b7dx?p=102-105

http://www.ai-start.com/ml2014/html/week10.html