【刷题系列】刷题总结（注意点、常用API、常见概念、常用技巧）

系列汇总：《刷题系列汇总》

个人LeetCode刷题总结

---

---

特别注意

• 编程第一步：优先考虑边界条件判断
• 接口不能实现（即不能实例化）：如List
• 递归时很多结构不能直接用"="赋值，否则会影响原结构值改变：包括二维数组、栈，list等等
• 泛型中要求完整英文，如 Integer、Character等
• 空字符串不等同于null："" != null
• 多个判断条件时一般把范围类、边界判断类的放前面，否则后面的条件会越界报错
• 位运算(& | ~ ^)符号的优先级低于==/!=，所以需要把位运算部分用括号框起来，例如：if((exponent & 1) == 1){}
• 手撕算法时，全局变量及子方法全部要加static

  public class Main {
  	static int res = 0; // 全局变量
      public static void main(String[] args) {}
      private static void judge(){} // 子方法
  }
  

• 二叉搜索树的中序遍历就是树节点值的递增排列 !!!
• StringBuilder可以直接append数字（或多个不同类型的组合）：如str.append(root.val + ",");
• HashSet的add函数：若元素不存在则添加，且返回true，否则返回false
  可用于同时添加元素和判断该元素是否存在
• 链表的特殊性：

• ① 输出其中一个节点的索引并不仅仅代表该节点node，而是代表node+node后面所有的节点 如node.next指的是当前节点的下一节点及其后面所有节点
• ② 链表节点不能直接进行比较， node1 == node2（X），可以比较节点值val

• do...while{}：专门用于那些需要至少运行一次的循环
• m位的数 * n位的数的结果位数一定在[m+n-1,m+n]之间
• BFS适合范围：涉及层序遍历、最短路径的问题
• 堆排序每次只排前一个，所以如果想正确取得所有排序结果，必须读一个抛一个。
• 遍历map前必需先确定包含对应的key，否则会抛出空指针异常

if(mapClose.containsKey(tarS)){
   for(int d:mapClose.get(tarS)){
       dfs(d,operation);
   }
}

• 输出堆排序结果时需注意：
  • 堆每次只排前一个，必须前面抛掉一个后一个才会是正确的排序。
  • 故不能使用for(int i : queue){}来遍历排序结果

---

1 常用API

1.1 Arrays类相关

• Arrays.copyOfRange(T[ ] original,int from,int to)：取出数组的某一段，左闭右开
• Arrays.sort(nums)：数组升序排列
• Arrays.equals(sum1,sum2)：比较两数组是否相同（不能用“==”）

1.2 HashMap相关

• 2种新建方式：

  // 方式1：新建带值map（键值对）
  Map pairs = new HashMap() {{ // 也可加泛型
      put(')', '(');
      put(']', '[');
      put('}', '{');
   }};
   
   // 方式2：新建空map
  HashMap<Character,Integer> map = new HashMap<>();//因为要存储的形式是“字母-出现位置”，所以泛型定位为
  

• 根据key获取value：

	getOrDefault(key,defaultValue); // 获取指定 `key` 对应对 `value`，如果找不到 `key` ，则返回设置的默认值。

高频：HashMap的3种遍历方式

• 1、遍历所有键：keySet()

  for(Integer key: map.keySet()){ }
  

• 2、遍历所有值：values()

  for(Integer value: map.values()){ }
  

• 3、遍历所有键值：entrySet()

  for(Map.Entry<Integer, Integer> entry : map.entrySet()){ // 如果键值都需要获取，这种方式比先遍历keySet()，再get对应value快
  	int key = entry.getKey();
  	int value = entry.getValue();
  }
  

1.3 ArrayList相关

• list.add(Object element) 向列表的尾部添加指定的元素。
• list.size() 返回列表中的元素个数。
• list.get(int index) 返回列表中指定位置的元素，index从0开始。

1.4 String/Char相关

• charAt() 取对应位置的字符
• substring(i1,i2) 取出该区间的字符串儿，注意左闭右开
• split(" ") 按指定字符进行字符串分割，返回一个String[]数组，如String[] strs = str.split(",");
• 判断char是否为数字：c<='9' && c >='0' 或 Character.isDigit(c)
• 判断char是否为字母：c<='z' && c >='a' 或 Character.isLetter(c)

1.5 栈相关

• 新建：Stack stack=new Stack();
• 方法：
  • push()：入栈
  • pop()：返回栈顶元素，并删除
  • peek()：返回栈顶元素，不删除
  • isEmpty()：判断是否为空

1.6 队列Queue相关

• 新建：通过LinkedList实现——Queue queue = new LinkedList();
• 添加元素：
  • add：增加一个元索， 如果队列已满，则抛出一个IIIegaISlabEepeplian异常
  • offer：添加一个元素并返回true，如果队列已满，则返回false
  • put： 添加一个元素，如果队列满，则阻塞
• 返回头元素：
  • element：返回队列头部的元素，如果队列为空，则抛出一个NoSuchElementException异常
  • peek：返回队列头部的元素，如果队列为空，则返回null
  • poll：移除并返问队列头部的元素，如果队列为空，则返回null``take：移除并返回队列头部的元素 如果队列为空，则阻塞
  • remove：移除并返回队列头部的元素，如果队列为空，则抛出一个NoSuchElementException异常

• add()和offer()区别：一般用offer()
add()和offer()都是向队列中添加一个元素。一些队列有大小限制，因此如果想在一个满的队列中加入一个新项，调用 add()
  方法就会抛出一个 unchecked 异常，而调用 offer() 方法会返回 false。因此就可以在程序中进行有效的判断！
• poll()和remove()区别： 一般用poll()
remove() 和 poll() 方法都是从队列中删除第一个元素。如果队列元素为空，调用remove() 的行为与 Collection
  接口的版本相似会抛出异常，但是新的 poll() 方法在用空集合调用时只是返回 null。因此新的方法更适合容易出现异常条件的情况。
• element() 和 peek() 区别：一般用peek()
element() 和 peek() 用于在队列的头部查询元素。与 remove() 方法类似，在队列为空时， element() 抛出一个异常，而 peek() 返回 null。

1.7 ListNode相关

• 新建小技巧： ListNode newNode = new ListNode(0,head);在原链表前补0生成新链表

1.8 优先级队列（堆）相关：注意堆每次只排前一个，必须前面抛掉一个后一个才会是正确的排序。

• 升序排列（小根堆）：
  写法1：PriorityQueue minHeap = new PriorityQueue<>((v1, v2) -> v1 - v2);
  写法2（默认即可）：PriorityQueue minHeap = new PriorityQueue<>();
• 降序排列（大根堆）：
  写法1：PriorityQueue maxHeap = new PriorityQueue<>((v1, v2) -> v2 - v1);
  写法2：手动重写compare()，优点是可拓展性强，可以各种花式改写

  private PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
      @Override
      public int compare(Integer o1, Integer o2) {
          return o2.compareTo(o1);
      }
  });
  

高频：堆的花式改写

• 方式1：堆可以存储各种各样的结构，例如数组、list等，下面的例子就是根据数组第二个元素的大小，升序摆放。

  PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
      public int compare(int[] m, int[] n) {
          return m[1] - n[1]; //根据数组第二个值的大小进行升序排列
      }
  });
  

• 方式1：可以根据外部条件对堆内元素进行排序，例如下面的例子就是提前统计好了每个字母的出现字数数组count，对字母的出现次数降序排列

  PriorityQueue<Character> queue = new PriorityQueue<Character>(new Comparator<Character>() {
      public int compare(Character letter1, Character letter2) {
          return counts[letter2 - 'a'] - counts[letter1 - 'a']; // 注意有count
      }
  });
  

1.9 队列（Queue）和栈（Stcak/Deque）的实现方式

• 队列：Queue<> stack = new LinkedList<>();
• 栈：注意区分Queue和Deque
  • ① Stack stack = new Stack();（线程安全）
  • ② Deque<> stack = new ArrayDeque<>();
  • ③ Deque<> stack = new LinkedList<>();

1.10 StringBuilder与StringBuffer区别

• StringBuffer支持并发操作，线性安全的，适合多线程中使用
• StringBuilder不支持并发操作，线性不安全的，不适合多线程中使用
• StringBuilder在单线程中的性能比StringBuffer高。

1.11 ArrayList和LinkedList的区别

• ArrayList：以数组实现的，遍历时很快，但是插入、删除时都需要移动后面的元素，效率略差
• LinkedList：以链表实现的，插入、删除时只需要改变前后两个节点指针指向即可，省事不少

1.12 Integer中valueOf()和parseInt()的区别

valueOf()返回的是Integer对象，parseInt()返回的是int

---

2 常见概念

2.1 二叉树的3种序列

• 前序：根左右
• 中序：左根右
• 后序：左右根

2.2 字典序

就是字典中的字母顺序，例如abcd→abdc

2.3 回文

正反读都一样，即中心对称的

2.4 子串和子序列的区别

字串连续，子序列可以不连续

2.7 深拷贝和浅拷贝

• 浅拷贝：两者共用一份内存地址，一个改变，另外一个跟着改变；
• 深拷贝：两者的内存地址是不一样的，互相独立的。

2.8 递归3条件和三要素

• 可以使用递归的3个条件：

  • 大问题可拆分为2个子问题：可递归
  • 子问题的求解方式和大问题一样：有相同基本操作
  • 存在最小子问题：可结束

• 递归三要素

  • 1、停止条件
  • 2、基本操作
  • 3、递归方式：注意有返回值的函数也可以进行不返回的递归+

2.9 最大堆、最小堆、最大-最小堆（Heap）

一种经过排序的完全二叉树，其中任一非终端节点的数据值均不大于（或不小于）其左子节点和右子节点的值。

• 最大堆（大根堆）：最大堆任何一个父节点的值，都大于等于它左右孩子节点的值。
• 最小堆（小根堆）：最小堆任何一个父节点的值，都小于等于它左右孩子节点的值。
• 最大-最小堆：集结了最大堆和最小堆的优点，是最大层和最小层交替出现的二叉树，即最大层结点的儿子属于最小层，最小层结点的儿子属于最大层。
• 以最大（小）层结点为根结点的子树保有最大（小）堆性质：根结点的值为该子树结点值中最大（小）项。

2.10 优先队列 PriorityQueue底层原理

优先级队列底层的数据结构是一颗二叉堆，二叉堆的结构如下：

• 二叉堆特点：
  • 二叉堆是一个完全二叉树
  • 根节点总是大于左右子节点（大顶堆），或者是小于左右子节点（小顶堆）。

2.11 各排序算法时间复杂度和空间复杂度

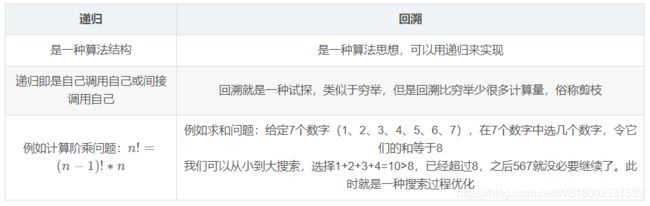
2.12 回溯和递归的区别

回溯可以用递归实现，可理解为“子状态不唯一的递归”（或者是“多分支的递归”）

2.13 二叉查找树（二叉搜索树，二叉排序树）：空/左 < 根 < 右/空

可以是一棵空树，或者是具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树。

2.14 “->” 分隔符（Lambda 表达式 / 闭包）

• Lambda 表达式：是推动 Java 8 发布的最重要新特性。Lambda 允许把函数作为一个方法的参数。使用 Lambda 表达式可以使代码变的更加简洁紧凑。Lambda 表达式的语法格式如下：

  (parameters) -> expression
  或
  (parameters) ->{ statements; }
  

• ->分隔符：Java 8新增的Lambda表达式中，变量和临时代码块的分隔符，即：(变量) -> {代码块}，如果代码块只有一个表达式，大括号可以省略。如果变量类型可以自动推断出来，可以不写变量类型。例如

  numbers.stream().filter(i -> i % 2 == 0); // 表示过滤符合条件{i % 2 == 0}的i，即流数据中的偶数项
  

2.15 双冒号操作符 :: 和 -> 的使用

• 方法调用：

person -> person.getAge()可以替换成Person::getAge
x ->System.out.println(x)可以替换成System.out::println

• 创建对象：

() -> new ArrayList<>();可以替换为ArrayList::new

注意：:: 的方法后面并没有()

---

3 常用技巧

3.1 求链表中点的方法

使用快慢指针的做法，快指针每次移动 2步，慢指针每次移动 1步，当快指针到达链表末尾时，慢指针指向的链表节点即为链表的中点。

3.2 怎么发现String中的多位连续数字并转换为int？

int num = 0；
for(int i = 0;i<s.length() && Character.isDigit(s.charAt(i));i++){
	num = 10*num + s.charAt(i) - '0';
}

3.3 DFS多方向遍历代码复用技巧：方向数组

DFS常需要搜索多个方向，分开写很麻烦，可以通过一个方向数组和循环搞定

• 方向数组：int[] dirs = {-1, 0, 1, 0, -1};
• 使用方法：仔细分析下就知道，相当于分别上、右、下、左移动

  for (int k = 0; k < 4; k++) {
  	int i_new = i_origin + dirs[k];
  	int j_new = j_origin + dirs[k + 1];
  }
  

3.4 ArrayList倒序添加小技巧

add(0,tempList); // 0表示插入的索引，保证总是将后面的插到前面

3.5 reverse()颠倒StringBuffer

new StringBuffer(str).reverse().toString();

3.6 计算一个数的各位数字之和

int sum = 0;
while(j != 0) {
	sum += j%10; // 计算个数
	j = j/10; // 原数字/10，于是原来的十位变成了新的个位
}

3.7 若堆的基本元素是数组，怎么读取堆顶数组的某个值

queue.peek()[1]; // 跟数组一样，利用索引读取 堆顶数组的第二个值

3.8 回溯法时变量会变的解决方法之一：新建一个变量用于遍历

for(int i : new HashSet<>(set1)){ // 为了不改变set1，故新建一个set1同值变量
    if(set2.size() >= 1 && pre - i > M) continue;
    set2.add(i);
    set1.remove(i);
    judge(set1,set2,N,M,i);
    set2.remove(i);
    set1.add(i);
}

3.9 对于两字符串，怎么按照字典序对其排列？/ 怎么进行多条件堆排序

s1.compareTo(s2);

PriorityQueue<String> maxHeap = new PriorityQueue<>(new Comparator<String>(){
    public int compare(String m,String n){
        return map.get(m) == map.get(n)? m.compareTo(n):map.get(n)-map.get(m); // 表示如果两字母出现次数相同，则按字典序排序，否则按出现次数排序
    }
});

3.10 已知根节点，如何寻找中序遍历（左-根-右）？

// 递归保存
ArrayList<TreeLinkNode> list = new ArrayList<>();
void InOrder(TreeLinkNode pNode){ // 调用时输入根节点
    if(pNode != null){ // 1.停止条件
    	// 2. 递归方式及操作
        InOrder(pNode.left); // 先存左子树
        list.add(pNode); // 再存根节点
        InOrder(pNode.right); // 最后存右子树
    }
}

3.11 怎么判断某节点开始的子树是否为BST（二叉搜索树，左<根<右）

BST

// 初始 min 为 Math.MIN_NALUE，max 为 Math.MAX_VALUE
boolean isBST(TreeNode root, int min, int max) {
    if (root == null) { // 停止条件
        return true;
    }
    return root.val > min && root.val < max && isBST(root.left, min, root.val) && isBST(root.right, root.val, max);
    // 即满足3个条件：
	// 1. 右子树的节点值大于根节点：`root.val > min`
	// 2. 左子树的节点值小于根节点：`root.val < max` 
	// 3. 所有的节点都满足上述两条件：`isBST(root.left, min, root.val) && isBST(root.right, root.val, max)`
	// 注意：对于左子树更新其最大值为当前节点值，对于右子树更新其最小值为当前节点值
}

3.12 怎么根据前序遍历和中序遍历还原二叉树？

前序遍历的第一个节点为根节点，中序遍历中根节点左边的部分为左子序列，右边的部分为右子序列

前序序列{1,2,4,7,3,5,6,8} = pre
中序序列{4,7,2,1,5,3,8,6} = in
1.根据当前前序序列的第一个结点确定根结点：为 1 找到 1 在中序遍历序列中的位置，为 in[3]
2.切割左右子树：in[3] 前面的为左子树， in[3] 后面的为右子树
–
下面很重要：
切割后的 中序子序列 b 长度 = 前序子序列 a 长度
所以 b 有多长，就要从 pre 第1个元素后面切割多长，这样才能对应的上
则切割后的左子树前序序列为：{2,4,7}，切割后的左子树中序序列为：{4,7,2}；
切割后的右子树前序序列为：{3,5,6,8}，切割后的右子树中序序列为：{5,3,8,6}

3.13 List<.List<.T>>定义方式

List> res = new ArrayList<>();//前面尽管有两层，后面一层即可

---