深度学习入门笔记1 感知器
深度学习
基本概念
- 深度学习是机器学习算法中的一类,其源于人工神经网络的研究。
- 深度学习广泛应用在计算机视觉,音频处理,自然语言处理等诸多领域。
- 深度可以理解为数据计算转换的层数。
机器学习&深度学习
深度学习可以看做是机器学习的一个研究领域(没有严格的定义)。目前,机器学习主要处理结构化数据,而深度学习主要处理非结构化数据。
神经元
深度学习从生物学中受到启发,其灵感来自于人脑的神经网络。 神经网络可以看做是由若干神经元构成。
神经元是大脑中相互连接的神经细胞。其可以处理和传递化学与电信号。

其中,树突用来接收信号(可能包含多个信号),如果累加的信号超过一定的阈值,经过细胞体的整合,就会生成一个输出信号,经过轴突传递给下一个神经元。也就是说,如果输入的信号超过一定的阈值,我们就可以认为神经元被激活,否则,我们可以认为神经元被抑制。
感知器
算法说明
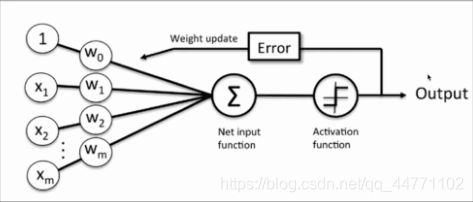
1957年,美国学者Frank Rossenblatt(弗兰克·罗森布拉特)提出了感知器(感知机)算法。感知器用来接收多个信号,输出一个信号(由多个神经元组成)。每个输入信号具有一定的权重,计算多个输入信号的值与权重的乘积和,根据该结果(和)与指定的阈值进行比较,来决定该神经元是否被激活。
说明:
- 感知器是神经网络起源的算法,该思想对于学习神经网络是非常具有指导意义的。
算法公式
根据感知器的定义可知,感知器可以实现二分类的任务。感知器的计算方式如下:
z = w 1 ∗ x 1 + w 2 ∗ x 2 + … … + w n ∗ x n = ∑ j = 1 n w j ∗ x j = w T ∗ x z = w_{1} * x_{1} + w_{2} * x_{2} + …… + w_{n} * x_{n}\\ \ \ = \sum_{j=1}^{n}w_{j} * x_{j} = w^{T} * x z=w1∗x1+w2∗x2+……+wn∗xn =j=1∑nwj∗xj=wT∗x
其中,z称为净输入(net input)。然而,这样的计算结果是一个连续的值,我们需要将结果转换为离散的分类值,因此,这里,我们使用一个转换函数,该函数称为激励函数(激活函数)。
s t e p ( z ) = { 1 z > = θ 0 z < θ step(z)=\left\{\begin{matrix} 1\ z >= \theta \\ 0\ z < \theta \end{matrix}\right. step(z)={1 z>=θ0 z<θ
这里, θ \theta θ就是阈值。
说明:
- 我们可以对阈值 θ \theta θ进行调整,使得阈值为0。
- 激活的条件,是>与<=,还是>=与<,没有明确的要求,二者都可以。
-
权重更新
感知器是一个自学习算法,即可以根据输入的数据(样本),不断调整权重的更新,最终完成分类。权重的更新公式如下:
w j = w j + Δ w j w_{j} = w_{j} + \Delta w_{j} wj=wj+Δwj
Δ w j = η ( y ( i ) − y ^ ( i ) ) x j ( i ) \Delta w_{j} = \eta (y ^ {(i)} - \hat{y} ^ {(i)}) x_{j}^{(i)} Δwj=η(y(i)−y^(i))xj(i)
其中,j表示某一列,i表示某一个样本。
更新原则
感知器的权重更新依据是:如果预测准确,则权重不进行更新,否则,增加权重,使其更趋向于正确的类别。
实现步骤
- 对权重进行初始化。(初始化为0或者很小的数值。)
- 对训练集中每一个样本进行迭代,计算输出值y。
- 根据输出值y与真实值,更新权重。
- 循环步骤2。直到达到指定的次数(或者完全收敛)。
说明:
- 如果两个类别线性可分,则感知器一定会收敛。
- 如果两个类别线性不可分,则感知器一定不会收敛。
程序示例
参考之前感知器的实现步骤,使用感知器实现与门与或门的计算。
与门
| x0 | x1 | x2 | y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
或门
| x0 | x1 | x2 | y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
练习
- 使用感知器实现或门的运算。
- 对上例使用不同的初始化权重,会得到什么结果?
import numpy as np
# 定义数据集
X = np.array([[1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]])
# 定义标签(每个样本所属的分类)。
y = np.array([0, 0, 0, 1])
# 定义权重。对于单层感知器,权重通常初始化为0或者很小的数值。
# w = np.zeros(3)
w = np.random.random(3)
# 定义学习率。
eta = 0.1
for epoch in range(7):
for x, target in zip(X, y):
# 计算净输入
z = np.dot(w, x)
# 根据净输入,计算分类值。
y_hat = 1 if z >= 0 else 0
# 根据预测值与真实值,进行权重调整。
w = w + eta * (target - y_hat) * x
# 注意数组的矢量化计算,相当于执行了以下的操作。
# w[0] = w[0] + eta * (y - y_hat) * x[0]
# w[1] = w[1] + eta * (y - y_hat) * x[1]
# w[2] = w[2] + eta * (y - y_hat) * x[2]
print(target, y_hat)
print(w)
感知器的局限
尝试使用感知器实现异或门,会得到怎样的结果。
| b | x1 | x2 | y |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
# 使用单层感知器无法实现异或门。
# 感知器的局限:如果两个类别的样本在空间中线性不可分,则感知器永远也不会收敛。
X = np.array([[1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]])
y = np.array([0, 1, 1, 0])
# w = np.zeros(3)
w = np.random.random(3)
eta = 0.1
for epoch in range(70):
for x, target in zip(X, y):
z = np.dot(w, x)
y_hat = 1 if z >= 0 else 0
w = w + eta * (target - y_hat) * x
print(target, y_hat)
print(w)
算法的Python实现
现在,我们使用Python语言来实现感知器算法,进行鸢尾花的分类。
class Perceptron:
"""通过Python语言实现感知器类。用来进行二分类任务。"""
def __init__(self, eta, epoch):
"""初始化方法。
Parameter:
-------
eta: float
学习率。
epoch: int
对训练集训练的轮数。
"""
self.eta = eta
self.epoch = epoch
def step(self, z):
"""阶跃函数。对净输入进行转换。
Parameter:
-----
z: 标量或数组类型
净输入。
Return:
------
t: 变量或数组类型。
分类的结果。0或者1。当z >= 0时,返回1,否则返回0。
"""
# return 1 if z >= 0 else 0
return np.where(z >= 0, 1, 0)
def fit(self, X, y):
"""训练方法。
Parameter:
X: 类数组类型。形状为 (样本数量, 特征数量)
提供的训练集。
y: 类数组类型。形状为(样本数量,)
样本对应的标签(分类)
"""
# 对类型进行转换,不管是什么二维类型,统一转换成二维的ndarray数组类型。
X = np.asarray(X)
y = np.asarray(y)
# 注意:权重的数量要比特征的数量多1。多出来的一个就是偏置。
self.w_ = np.zeros(X.shape[1] + 1)
# 定义损失列表。用来存放每个epoch迭代之后,分类错误的数量。
self.loss_ = []
# 迭代epoch指定的轮数。
for i in range(self.epoch):
# 用来记录单次epoch的损失值(分类错误的数量)
loss = 0
for x, target in zip(X, y):
# 计算净输入
z = np.dot(x, self.w_[1:]) + self.w_[0]
# 根据净输入,计算分类。
y_hat = self.step(z)
# if target != y_hat:
# loss += 1
loss += target != y_hat
# 调整权重
self.w_[1:] += self.eta * (target - y_hat) * x
# 调整偏置
self.w_[0] += self.eta * (target - y_hat)
# 将损失值加入到损失列表当中。
self.loss_.append(loss)
def predict(self, X):
"""预测方法。根据提供的数据集X,返回每一个样本对应的标签(分类)。
Parameter:
-----
X: 类数组类型。形状为 (样本数量, 特征数量)
提供预测集。
Return:
-----
label: 类数组类型。形状为:(样本数量,)
预测的每一个便签分类。
"""
X = np.asarray(X)
# 计算净输入。(矢量化计算,没有使用循环分别对每一个样本求净输出)
z = np.dot(X, self.w_[1:]) + self.w_[0]
# 获取最终的分类结果。(一维数组类型。)
result = self.step(z)
return result
# 感知器类进行测试。
X = np.array([[1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]])
y = np.array([0, 0, 0, 1])
p = Perceptron(0.1, 7)
p.fit(X, y)
print(p.w_)
print(p.loss_)
练习
- 使用感知器对鸢尾花的后两个类别进行分类。
- 使用Python实现train_test_split方法的功能。