python自然语言处理—RNN(循环神经网络)

                                                              RNN(循环神经网络)

 

一、前言

    循环神经网络（recurrent neural network）源自于1982年由Saratha Sathasivam 提出的霍普菲尔德网络。

    传统的机器学习算法非常依赖于人工提取的特征，使得基于传统机器学习的图像识别、语音识别以及自然语言处理等问题存在特征提取的瓶颈。而基于全连接神经网络的方法也存在参数太多、无法利用数据中时间序列信息等问题。随着更加有效的循环神经网络结构被不断提出，循环神经网络挖掘数据中的时序信息以及语义信息的深度表达能力被充分利用，并在语音识别、语言模型、机器翻译以及时序分析等方面实现了突破。

二、定义

    1、语言定义：

        循环神经网络（Recurrent Neural Network, RNN）是一类以序列（sequence）数据为输入，在序列的演进方向进行递归（recursion）且所有节点（循环单元）按链式连接的递归神经网络（recursive neural network）。

    2、数学定义：

        输入为  对应的隐藏状态 

        输出为 

        则经典 RNN 的运算过程可以表示为：

            

            

            

            其中  均为参数， 为 时间步(time-step)，而  表示激活函数，一般为  函数。

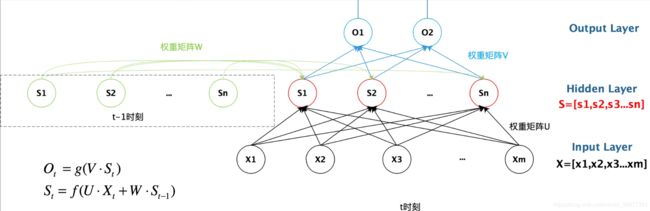
三、RNN 模型

    循环神经网络的主要用途是处理和预测序列数据。在全连接神经网络模型和卷积神经网络模型中，网络结构都是从输入层到隐藏层再到输出层，层与层之间是全连接或部分全连接的，但每层之间的节点是无连接的。考虑这样一个问题，如果要预测句子的下一个单词是什么。一般需要用到当前单词以及前面的单词，因为句子中前后单词并不是独立的。比如，当前单词是 "很"，前一个单词是 "天空"，那么下一个单词很大概率是 "蓝"。循环神经网络的来源就是为了刻画一个序列当前的输出与之前信息的关系。从网络结构上，循环神经网络会记忆之前的信息，并利用之前的信息影响后面节点的输出。也就是说，循环神经网络的隐藏层之间的节点是有连接的，隐藏层的输入不仅包括输入层的输出，还包括上时刻隐藏层的输出。

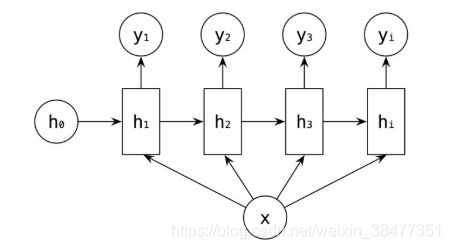
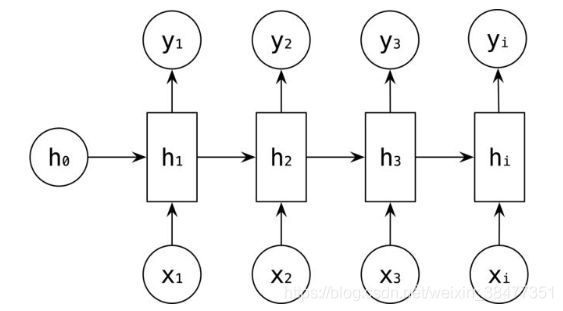
    1、RNN 结构图如下：

        

        

        左图：RNN 模型未按时间序列展开的图。

        右图：RNN 模型按时间序列展开的图。

        图描述了在序列索引号  附近 RNN 的模型。其中：

            （1） 代表在序列索引号  时训练样本的输入。 同样的， 和  代表在序列索引号  和  时训练样本的输入。

            （2） 代表在序列索引号  时模型的隐藏状态。 由  和  共同决定。

            （3） 代表在序列索引号  时模型的输出。 只由模型当前的隐藏状态  决定。

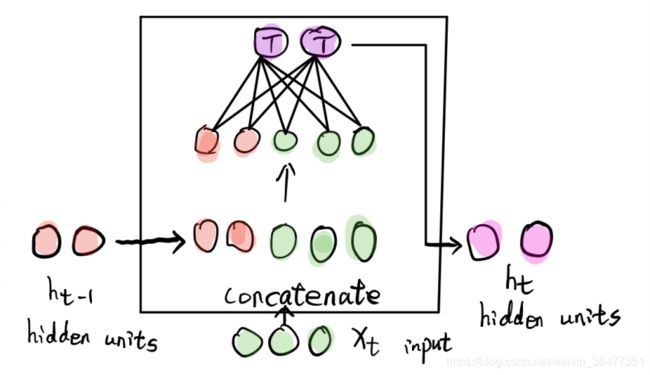
    2、常用计算

        (1) 加法(addition)

           

        (2) 乘法(multiplication)

            

        (3) 连结(concatenate)

            

    3、 计算逻辑图

        

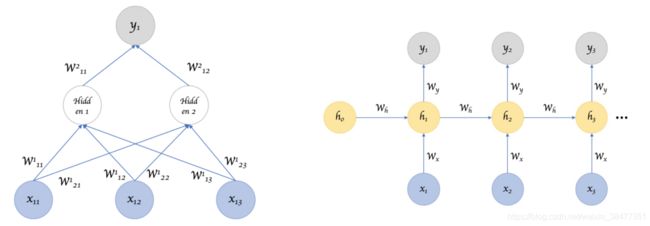
    4、参数共享(parameter sharing)

        

        左图：普通神经网络，不共享参数。

        右图：RNN 神经网络，共享参数。

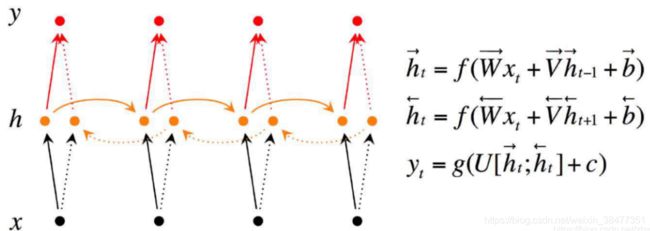
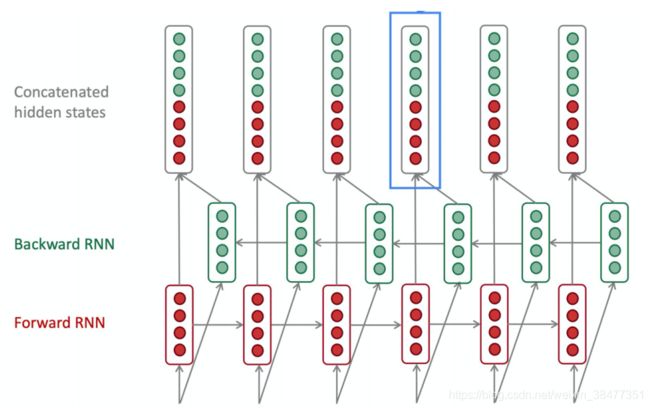
    5、双向 RNN(Bidirectional RNNs)

        时间步  的输出不仅取决于之前时刻的信息，还取决于未来时刻的信息，所以有了双向 RNN。比图要预测一句话中间丢失的一个单词，有时只看上文是不行的，需要查看下文。双向 RNN 其实就是两个相互叠加的 RNN。

                   

        从上图可以看出，每个时刻有一个输入，隐藏层有两个节点（向量），一个  进行正向计算，另一个  进行反向计算，输出层由这两个值决定。

        计算公式：

            

            

            

        从式子中可以看出，正向计算和反向计算的权重不共享，即一个单层的双向 RNN 一共有6个权重矩阵： 正向：、、；反向：、、；三个权重向量：、、。

        应用场景：

            a、完形填空。

            b、机器翻译。

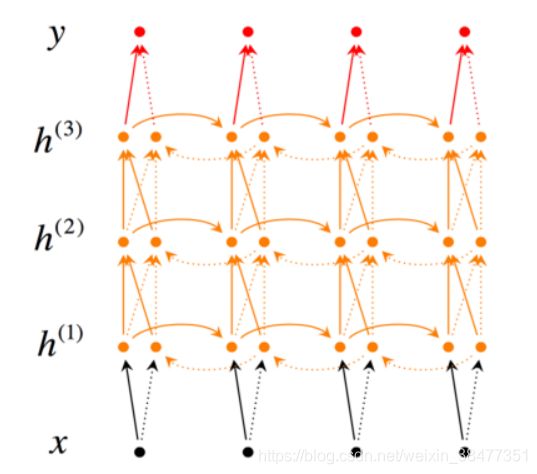
    6、深层双向 RNN(Deep RNNS)

        和双向RNN类似，只是每个时刻有多个层。层数越多，学习能力越强，但也需要更多训练数据。

        相对于普通 DNN 隐藏层可能有上百层之多，而 RNN 有 3 层就算多了，因为有时间维度，网络会变得相当大，即使只有很少的隐藏层。 通常会在输出层：，加上比较深的层，但是这些层在水平方向上并不相连。        

        深层双向 RNN 常见的一种结构图如下：

            

        我们用上标  来表示第  层，按图中的上下顺序给出计算公式：

            

            

            

            

            

                   

 四、RNN 神经网络模型的不同结构

    RNN( Recurrent Neural Network 循环(递归)神经网络) 跟人的大脑记忆差不多。我们的任何决定、想法都是根据我们之前已经学到的东西产生的。RNN 通过反向传播和记忆机制，能够处理任意长度的序列，在架构上比前馈神经网络更符合生物神经网络的结构，它的产生也正是为了解决这类问题而应用而生的。这里介绍 RNN 的几种不同的结构：

    1、one-to-one RNN 结构

       

        这是 RNN 最基本的单层网络，输入是 ，经过变换  和 激活函数  得到输出 。

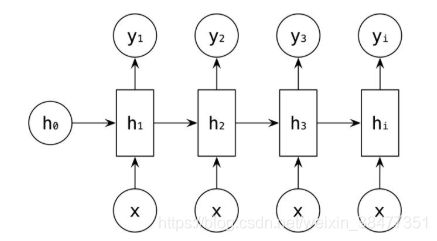
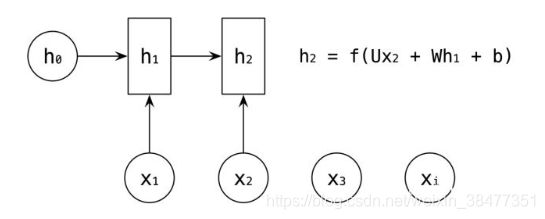
    2、one-to-many RNN 结构

        

        一对多结构：输入不是序列，输出为序列，只在序列开始时进行输入计算。比如：看图说话，从图片中生成文字描述，当输入的  是图像的特征，输出是一段句子，即序列 。

        另一种结构：将信息输入  作为每一阶段的输入，如下图所示：

            

        上图也可以用下图等价表示：

            

        应用场景：

            （1）从图像生成文字（image caption），此时输入的是图像的特征，而输出为一段句子（序列）。

            （2）从类别生成语言或音乐等。

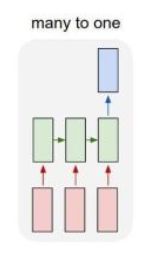
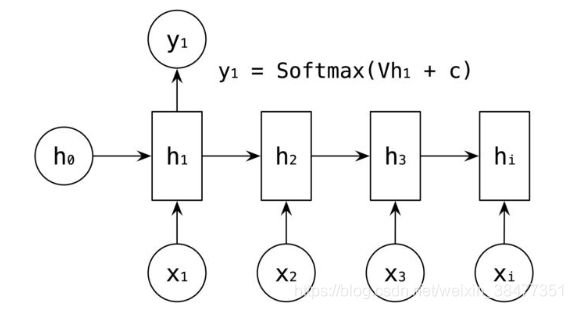
     3、many-to-one RNN 结构

        

        多对一结构：输入一个序列，输出一个单独的值。

        应用场景：

            （1）这种结构通常用来处理序列分类问题。如输入一段文字判别所属的类别、输入一个一个句子判断其情感倾向、输入一段视频来判断它的视频类别等。

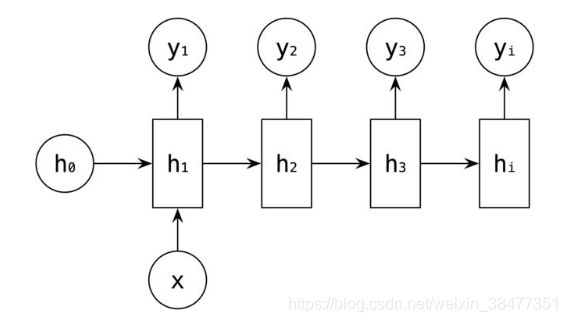
    4、many-to-many RNN 结构

        （1）输入 == 输出

            

            多对多是 RNN 中最经典的结构，其输入、输出都是等长的序列数据。假设输入 ，每个  为一个单词的词向量。

                

            RNN 中引入了隐藏层（hidden state），隐藏层的作用是用来对序列数据提取特征，接着再转换为输出。如下图所示， 的计算是由输入  和 ，经过变换  和 激活函数 得到输出 。

                

              的计算和  类似，在计算时，每一步使用的参数  都是一样的，也就是说每个步骤的参数都是共享的，这是 RNN 的一个重要特点：参数共享。

                

            依次计算剩下的 ，使用相同的参数  。

                

            输出值的计算，是通过  进行计算，如  的输出值是通过对  进行一次  变换和激活函数  得到输出 。

                 

            剩下的  的输出使用类似的方式进行计算。

                

            应有场景：

                a、序列标注。

                b、计算视频中每一帧的分类标签，对每一帧进行计算，输入和输出序列等长。

        （2）输入 !== 输出

            

            应用场景：

                a、机器翻译，输入一个文本，输出另一种语言的文本。