机器学习（三）——sigmoid函数和SVM的基本型

为了解决符号函数面对分类问题时的解不唯一、受离群点影响大的问题，我们就想用一种新的方法来对数据分类。为此，我们使用一个新的将数据分开的函数——sigmoid函数。
$$h_{\omega ,b}(x)=\frac{1}{1+e^{-(\omega x+b)}}$$它的图像大概是这样的($\omega =1,b=0$)
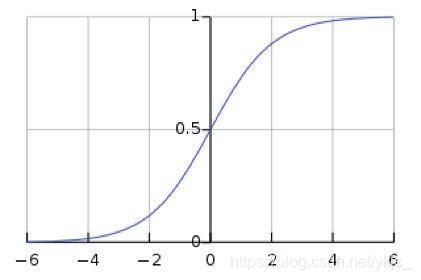对于这样一个函数，当函数值大于0.5时，我们就将其划分至有1的特征的这一类，当函数值小于等于0.5时，我们就将其划分至有0的特征的这一类。
和之前一样，我们可以为训练集的输入变量增加一组特征1，就可以将$b$作为$\omega$中的一个分量进行处理
接下来就是针对这一分类方法找到一个凸的代价函数(证明见这里)
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}ln{h}_{\omega }(x^{(i)})+(1-y^{(i)})ln(1-h_{\omega }(x^{(i)}))$$上式即我们找到的关于数据集分类的凸的代价函数，我们就可以利用梯度下降或是随机梯度下降来找到令代价函数最小化的一组$\omega$
梯度下降
$${\omega }_j={\omega }_j-\eta \sum _{i=1}^m(h_{\omega }(x^{(i)})-y^{(i)})x_j^{(i)},j=0,1,\cdots ,n$$随机梯度下降
$${\omega }_j={\omega }_j-\eta (h_{\omega }(x^{(i)})-y^{(i)})x_j^{(i)},j=0,1,\cdots ,n$$
这样我们能够得到一个很好的线性分类器。

但是面对线性不可分的数据，单单凭借之前的感知机或是sigmoid函数是不行的，然而再线性回归中，当单变量回归不足以很好地描述数据时，我们采用了将数据映射到高维上，再采用单变量线性回归处理的方法，即多变量线性回归。类比一下，我们也同样可以设置维数来将数据映射到高维上，再采用之前的方法来对数据分类。支持向量机SVM算法的核函数技巧就使用了类似的思路来帮助我们解决这个问题。
为简单起见，我们先介绍一下SVM对线性可分数据的处理的基本型：
面对一组线性可分的数据，我们有无数组超平面能够划分它们，那么哪组分类的效果更好呢？
对于SVM，这个问题的答案是：能够让两类数据中离这条直线最近的两点(两类数据中各一个)到这条直线的距离相等且相较于取其他直线时该距离最大，满足以上条件的直线即为SVM所求的直线。如下图所示

假设目标的超平面为
$${\omega }^{T}x+b=0$$那么点$x^{(i)}$到直线的距离$d$即为$$d=\frac{|{\omega }^{T}x+b|}{||\omega ||}$$由于超平面的方程为等式，我们可以等比例放大或是缩小$\omega$、$b$来使得距离$d$变成$$d=\frac{1}{||\omega ||}$$这样的话，两组数据就可以表示成$${\omega }^{T}x+b\ge 1$$$${\omega }^{T}x+b\le -1$$再进一步，将大于等于1的数据取特征1，小于等于-1数据取特征-1$$y^{(i)}({\omega }^{T}x+b)\ge 1$$我们的优化目标就是$$max\frac{1}{||\omega ||}$$$$s.t.y^{(i)}({\omega }^T{x}^{(i)}+b)\ge 1,i=1,2,\cdots ,n$$当前目标函数不是凸函数，不易优化，我们改写一下$$min\frac{1}{2}||\omega |{|}^2$$$$s.t.y^{(i)}({\omega }^T{x}^{(i)}+b)\ge 1,i=1,2,\cdots ,n$$现在的目标函数为凸函数，即为SVM的标准型。