2022第13届蓝桥杯C++A组(记录)
今天参加了蓝桥杯的比赛,感觉除了最后一道题写完后,差一点点没有运行成功,别的也没什么遗憾了,在算法刷题方面自己起步较晚,刷题较少,但是今天依旧做出了两道填空题(今年采取线上,一共只有两道填空题目),和5道编程题(一共8道),比赛刚刚结束,也没有公布答案,不知对错,先写一篇博客放松一下,一会儿再去制定下一步的计划……
A题:
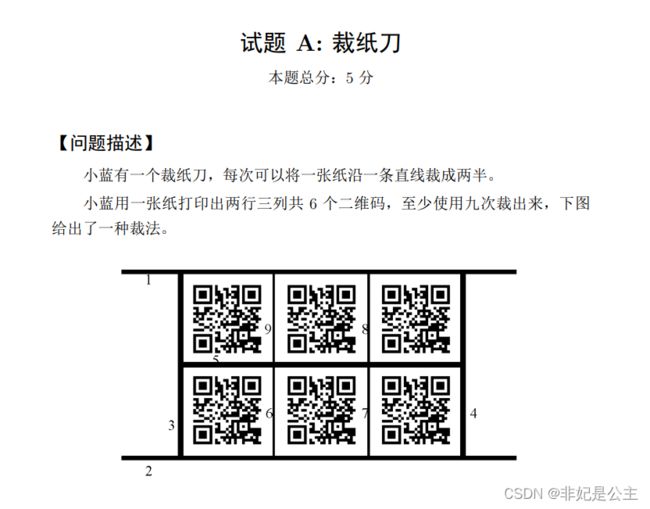
题目并不难,分为三个部分,首先切割四个边,然后切割行,最后将每一行切成块。下面是我计算的过程。
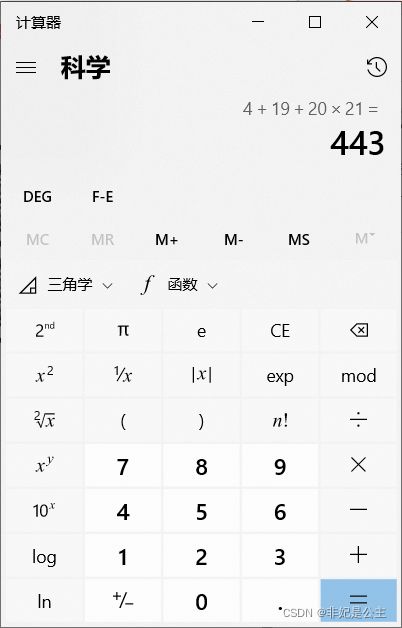
B题:

比赛时这道题我还想了一阵,后来发现了解法,其实很简单,如果小乔(后放的人)每次都和小蓝(后放的人)对着放,那么无论小蓝怎么放,小乔都可以有位置去放,最终填满棋盘获胜。所以答案自然是“LLLL”。
C题:
#include根据测试用例,n的最大值为200000,ai的最大值为1000,假设我们都考虑最大值。也就是200000个数中进行排列有C2000002种方式,每种方式都为1000×1000,结果如下图所示:
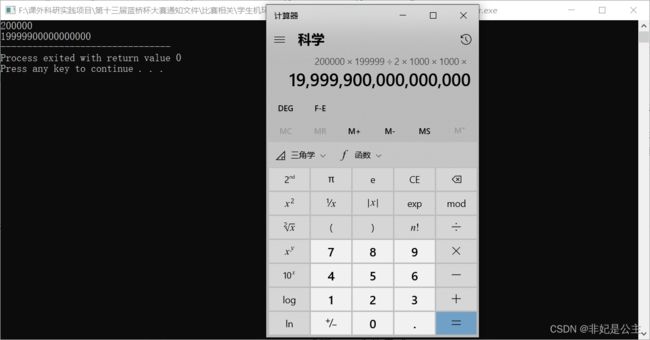
可以发现,对于最大的数,unsigned long long没有越界,证明我们的程序对测试数据规模是没有问题的。(比赛的时候还在想是不是要用string去存储)
D题:
#includeE题:
F题:
比赛时没有写出,当时考虑应该用回溯去做,出考场后和同学讨论,发现有同学在用贪心的方法去做,从10000开始,每次递减。

G题

这道题利用了动态规划的思想,保留了两个数组tmp1和tmp2,tmp1[i]表示第i位往前最长不下降子序列的数量,tmp2[i]表示第i位往后数最长不下降子序列。然后就是中间插k位,进行一定的边界处理。
#includeH题:

将每个点位从近到远排序,然后判断是否会存在并列的情况,依据相似三角形对应边成比例进行判断。但是后面发现这种做法存在问题,就是没有考虑到点位的角度信息,很有可能是远的点比近的点先碰到,所以这种做法应该只能通过一部分测试用例。
#includeI题:
这道题也没有思路,但是出考场后与同学交流,听到有用四层for循环去通过测试用例的顿时,眼前一亮,当时自己怎么没有想到。

J题:

这道题主要利用了set,创建集合,将已知的部分和一个一个装入,每装入一个要判断和集合内的元素是否可以构成新的部分和。这可以将所有可能的情况列出,询问时,我们只需要进行集合中的查找即可。
情况1:当前插入部分和与集合中现有的某一个部分和重合,且有一个端点重合。
情况2:当前插入部分和与现有某一部分和不重合,且有一个端点重合。
这是比赛时我画的一个图,如下:

哈哈,是不是很抽象,这块明白了感觉非常简单,不明白越说越乱,读者可以对照代码以及我上面写的思路稍微进行一点思考,应该就可以搞明白了。
最后的最后,其实在这里有一点小遗憾,在利用自定义类型的set模板时,在运算符重载的位置遇到了一些困难,主要是const问题,还有set是由二叉树构建的,所以需要重载==和<运算符,导致最后时间十分紧张,打错了一个变量,导致程序是错误的,有些遗憾,但是这可能也是实力的一种体现吧。自己在算法方面确实还有待加强,毕竟计算机可是靠算法吃饭的呀。
#include最后,此次蓝桥杯比赛也算是结束了,感受到了这学期刷题以来的进步,但是也看到了自己还有很大的提升空间。刷题还是要坚持下去的,平日里还是要坚持去做一些事情,做长远投资。


