灰色预测模型GM(1,1)
本文参考的是司守奎,孙兆亮主编的数学建模算法与应用(第二版)
灰色预测的主要特点时模型使用的不是原始数据序列,而是生成的数据序列。其核心体系时灰色模型,即对原数据作累加生成得到近似指数规律再进行建模的方法。
优点:不需要很多数据,一般只需要4个数据,就能够解决历史数据少。序列的完整性及可靠性低的问题,能利用微分方程充分挖掘系统的本质,精度高;能将无规律的原始数据进行生成得到规律性较强的生成序列,运算简便,便于检验,不考虑分布规律,不考虑变化趋势。
缺点:只使用于中短期的预测,只适合指数增长的预测。
下面介绍使用GM(1,1)的一般步骤。
1.数据的检验与处理,需要进行数据的级比校验,只有级比校验通过才适合灰色预测,要是没通过,可以通过取适当的常数c作平移变换(不过我觉得,没通过就别用了吧)。

2.建立模型

3.检验预测值。残差检验和级比残差值检验都通过模型才视作有效。

4.使用模型预测

由于灰色预测模型是根据序列来预测的,预测希望预测第几个值,直接输入对于序列即可。
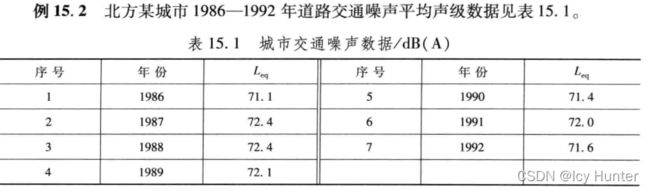
x0 = [71.1 72.4 72.4 72.1 71.4 72.0 71.6]';% 这里为列向量
n = length(x0);
lamda = x0(1:n-1)./x0(2:n); %计算级比(前一个数/后一个数,共六个)
range = minmax(lamda')%级比范围
range_min = exp(-2/(n+1));
range_max = exp(2/(n+2));
if range_min <= range(1) && range_max >= range(2)
fprintf("级比检验通过")
else
fprintf("级比检验失败")
end
x1 = cumsum(x0); %累加计算x(1)
B = [-0.5*(x1(1:n-1) + x1(2:n)), ones(n-1,1)];
Y = x0(2:n);
u = B\Y
syms x(t)
x = dsolve(diff(x) + u(1)*x == u(2), x(0) == x0(1));%求微分方程的符号解
xt = vpa(x, 6) %以小数格式显示微分方程的解
yucel = subs(x,t,[0:n-1]);%求已知数据的预测值
yucel = double(yucel);%符号数转换成数值类型,否则无法做差分运算
yuce = [x0(1), diff(yucel)] %差分运算,还原数据
epsilon = x0' - yuce;% 计算残差
delta = abs(epsilon./x0');%计算相对误差
rho = 1 - (1 - 0.5 * u(1))/(1 + 0.5 * u(1)) * lamda';%计算级比偏差值,u(1)=a
4.使用模型预测。带入模型计算即可。
m = 8 %m=用于训练模型的数据个数 + 希望往后预测的个数
y = subs(x, t, [0:m])
y = double(y);
y_pre = [x0(1), diff(y)]
matlab完整代码如下:
clc,clear
x0 = [71.1 72.4 72.4 72.1 71.4 72.0 71.6]';% 这里为列向量
n = length(x0);
lamda = x0(1:n-1)./x0(2:n); %计算级比(前一个数/后一个数,共六个)
range = minmax(lamda');%级比范围
range_min = exp(-2/(n+1));
range_max = exp(2/(n+2));
if range_min <= range(1) && range_max >= range(2)
fprintf("级比检验通过")
else
fprintf("级比检验失败")
end
x1 = cumsum(x0); %累加计算x(1)
B = [-0.5*(x1(1:n-1) + x1(2:n)), ones(n-1,1)];
Y = x0(2:n);
u = B\Y;
syms x(t)
x = dsolve(diff(x) + u(1)*x == u(2), x(0) == x0(1));%求微分方程的符号解
xt = vpa(x, 6) %以小数格式显示微分方程的解
yucel = subs(x,t,[0:n-1]);%求已知数据的预测值
yucel = double(yucel);%符号数转换成数值类型,否则无法做差分运算
yuce = [x0(1), diff(yucel)] %差分运算,还原数据
epsilon = x0' - yuce;% 计算残差
delta = abs(epsilon./x0');%计算相对误差
rho = 1 - (1 - 0.5 * u(1))/(1 + 0.5 * u(1)) * lamda';%计算级比偏差值,u(1)=a
m = 8; %m=用于训练模型的数据个数 + 希望往后预测的个数
y = subs(x, t, [0:m]);
y = double(y);
y_pre = [x0(1), diff(y)]