【python机器学习】逻辑回归算法实现(基于鸢尾花数据集)
注意
逻辑回归是分类模型!!!
本次实验我们做二分类任务,鸢尾花数据集有三个分类,那我们需要选择两个类。
逻辑回归内部也使用梯度下降算法
数据集资源
本文基于鸢尾花 数据集实现
数据集:数据集网盘下载
提取码:p2v9
数据集简单处理
import numpy as np
import pandas as pd
data = pd.read_csv(r"dataset/iris.arff.csv")
#data
# 删除重复记录
data.drop_duplicates(inplace=True)
# Iris-setosa Iris-versicolor Iris-virginica
data["class"] = data["class"].map({"Iris-versicolor":0,"Iris-setosa":1,"Iris-virginica":2 })
# 只选取类别为0与1的鸢尾花数据,进行逻辑回归的二分类
data = data[data["class"] != 2]
# len(data) #98
逻辑回归代码实现
class logisticRegression:
"""使用python语言实现逻辑回归算法"""
def __init__(self,alpha,times):
"""初始化方法
Parameters:
alpha:float
学习率
times:int
迭代次数
"""
self.alpha = alpha
self.times = times
def sigmoid(self,z):
"""sigmoid函数的实现
Parameters:
z:float
自变量,值为z = w.T * x
Return:
p: float,值为[0,1]之间
返回样本属于类别1的概率值,用来作为结果的预测。
当x>=0.5(z>=0),判定为类别1;否则,判定为类别0.
"""
return 1.0 / (1.0 + np.exp(-z))
def fit(self,X,y):
"""根据提供的训练数据,对模型进行训练。
Parameters:
X:类数组类型。形状为:[样本数量,特征数量]
待训练样本的特征属性矩阵。
y:类数组类型。形状为:[样本数量]
每个样本的目标值。(标签)
"""
X = np.asarray(X)
y = np.asarray(y)
#初始化权重向量,注意:w_的长度比特征数多1(为截距)。
self.w_ = np.zeros(1 + X.shape[1])
# 创建损失列表,用来保存每次迭代后的损失值
self.loss_ = []
for i in range(self.times):
z = np.dot(X,self.w_[1:]) + self.w_[0]
# 计算概率值
p = self.sigmoid(z)
# 根据逻辑回归的代价函数,计算损失值
# 逻辑回归的目标函数
# J(w) = -sum(yi * log(s(zi))+(1-yi)*log(1-s(zi))) {i从1到n,n为样本数量}
cost = -np.sum(y * np.log(p) + (1 - y)*np.log(1-p))
self.loss_.append(cost)
# 调整权重值,根据公式调整为:权重(j列) = 权重(j列) + 学习率*sum((y - s(z))*x(j))
self.w_[0] += self.alpha * np.sum(y - p)
self.w_[1:] += self.alpha * np.dot(X.T,y-p)
def predict_proba(self,X):
"""根据参数传递的样本,对样本数据进行预测。
Parameters:
X:类数组类型。形状为:[样本数量,特征数量]
待测试样本特征(属性)
Return:
result:数组类型
预测的结果(概率值)
"""
X = np.asarray(X)
z = np.dot(X,self.w_[1:]) + self.w_[0]
p = self.sigmoid(z)
# 将预测结果变成二维结构,便于后续的拼接
p = p.reshape(-1,1)
# 将2个数组进行拼接,方向是横向的拼接
return np.concatenate([1-p,p],axis=1)
def predict(self,X):
"""根据参数传递的样本,对样本数据进行预测。
Parameters:
X:类数组类型。形状为:[样本数量,特征数量]
待测试样本特征(属性)
Return:
result:数组类型
预测的结果(类别)
"""
return np.argmax(self.predict_proba(X),axis=1)
数据打散&构建训练集与测试集
t1 = data[data["class"] == 0]
t2 = data[data["class"] == 1]
t1 = t1.sample(len(t1),random_state=0)
t2 = t2.sample(len(t2),random_state=0)
train_X = pd.concat([t1.iloc[:40,:-1], t2.iloc[:40,:-1]],axis=0)
train_y = pd.concat([t1.iloc[:40,-1], t2.iloc[:40,-1]],axis=0)
test_X = pd.concat([t1.iloc[40:,:-1], t2.iloc[40:,:-1]],axis=0)
test_y = pd.concat([t1.iloc[40:,-1], t2.iloc[40:,-1]],axis=0)
训练&预测
注意:虽然应用了梯度下降算法,但与上一讲【python机器学习】线性回归–梯度下降实现(基于波士顿房价数据集) 不同的是,鸢尾花数据集每个特征列的数量级都一样,所以不用标准化。
lr = logisticRegression(alpha=0.01,times=20)
lr.fit(train_X,train_y)
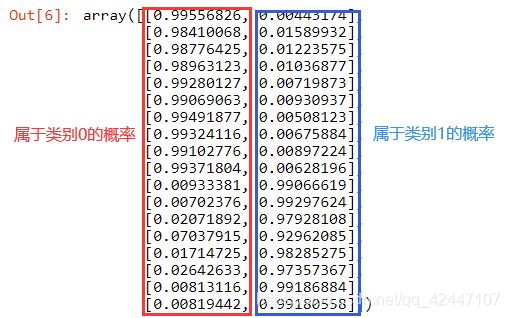
预测的概率值
#预测的概率值
lr.predict_proba(test_X)
预测的类别
#预测的类别
lr.predict(test_X)
![]()
计算准确度
#计算准确度
result = lr.predict(test_X)
print(np.sum(result == test_y)) #18个
print(np.sum(result == test_y)/len(test_y))
可视化
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False
# 绘制预测值
plt.plot(result,"ro",ms=15,label="预测值")
# 绘制真实值
plt.plot(test_y.values,"go",label="真实值")
plt.title("逻辑回归")
plt.xlabel("样本序号")
plt.ylabel("类别")
plt.legend()
plt.show()
# 发现全部"中靶"
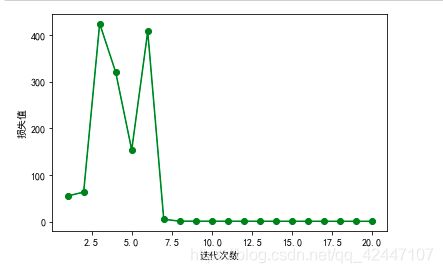
绘制损失值
# 绘制损失值
plt.plot(range(1,lr.times+1),lr.loss_,"go-")
plt.xlabel("迭代次数")
plt.ylabel("损失值")
plt.show()