从零实现深度学习框架——RNN从理论到实战【理论】
引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不使用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
本文介绍RNN,一种用于处理序列数据的神经网络。
循环神经网络
循环神经网络(Recurrent Neural Network,RNN)是包含循环连接的网络,即有些单元是直接或间接地依赖于它之前的。
本文我们学习一种叫做Elman网络的循环网络,或称为简单循环网络(本文中的RNN都代表该网络)。隐藏层包含一个循环连接作为其输入。即,基于当前输入和前一时刻隐藏状态计算当前隐藏状态。
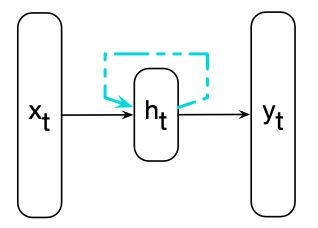
上图展示了RNN的结构,与普通前馈网络一样,表示当前输入 x t x_t xt的向量乘以权重矩阵,然后经过非线性激活函数来计算隐藏单元的值 h t h_t ht。然后用于计算相应的输出 y t y_t yt。
该网络在处理序列时,一次(一个时间步)顺序地处理序列中的一个元素,与我们之前看到的基于窗口的方法不同。我们使用下表来表示时间,这样, x t x_t xt表示时刻(时间步) t t t的输入向量 x x x。与前馈网络的关键区别在于上图虚线显示的循环连接。此连接使用上一个时刻隐藏层的值来增强对于当前时刻隐藏层计算的输入。
前一时刻的隐藏层提供了一种记忆(或上下文)的功能,可以提供之前的信息为未来做决定提供帮助。重要的是,这种方法理论上不需要对前文的长度进行限制,不过实际上过远的信息很难有效的保留。
前向传播
RNN中的前向传播(推理)过程和前馈网络差不多。但在使用RNN处理一个序列输入时,需要将RNN按输入时刻展开,然后将序列中的每个输入依次对应到网络不同时刻的输入上,并将当前时刻网络隐藏层的输出也作为下一时刻的输入。
为了计算时刻 t t t的输入 x t x_t xt对应的输出 y t y_t yt(图中是 o t o_t ot),我们需要先计算隐藏状态 h t h_t ht。为了计算它,让输入 x t x_t xt乘以权重矩阵 W W W以及前一时刻的隐藏状态 h t − 1 h_{t-1} ht−1乘以权重矩阵 U U U。然后把它们的结果加起来,并经过一个激活函数 g g g,通常为 tanh \tanh tanh函数,计算当前的隐藏状态 h t h_t ht。此时,我们可以通过 h t h_t ht来生成输出向量 y t y_t yt:
h t = g ( U h t − 1 + W x t ) y t = f ( V h t ) (1) \begin{aligned} h_t &= g(Uh_{t-1} + Wx_t) \\ y_t &= f(Vh_t) \end{aligned} \tag 1 htyt=g(Uht−1+Wxt)=f(Vht)(1)
(为了理解方便,没有写出偏置项,实际上每个矩阵乘法都可以带一个偏置项)
这里要注意维度。我们用 d i n , d h , d o u t d_{in},d_{h},d_{out} din,dh,dout分别代表输入、隐藏和输出层的大小。那么这三个权重矩阵的维度是: W ∈ R d h × d i n , U ∈ R d h × d h , V ∈ R d o u t × d h W \in \Bbb{R}^{d_h \times d_{in}}, U \in \Bbb{R}^{d_h \times d_h},V \in \Bbb{R}^{d_{out} \times d_h} W∈Rdh×din,U∈Rdh×dh,V∈Rdout×dh。
如果是多分类问题, y t y_t yt由 softmax \text{softmax} softmax函数计算而成:
y t = softmax ( V h t ) (2) y_t = \text{softmax}(Vh_t) \tag 2 yt=softmax(Vht)(2)
可以看到,时刻 t t t的计算需要啊前一个时刻 t − 1 t-1 t−1的隐藏层激活值(隐藏状态)。显然,这是一种递归形式的定义,从序列开始到序列结束。每个时刻的输入经过层层递归,对最终的输出产生一定影响,每个时刻的隐藏状态 h t h_t ht承载了 1 ∼ t 1\sim t 1∼t时刻的全部输入信息,因此循环神经网络中的隐藏单元也被称为记忆单元。
上图简单神经网络的前向推理。注意,矩阵 U , W , V U,W,V U,W,V在每个时刻都是共享的,每个时刻都会计算一个 h i h_i hi和 y i y_i yi。
这里初始时隐藏状态 h 0 = 0 h^0=0 h0=0。
学习
我们有三个权重要更新:输入层到隐藏层的权重 W W W;前一时刻隐藏层到当前时刻隐藏层的权重 U U U;隐藏层到输出层的权重 V V V。
但更新时与前馈网络不同,主要有两点。一,为了计算时刻 t t t的损失,我们需要时刻 t − 1 t-1 t−1的隐藏状态;二,时刻 t t t的隐藏状态同时影响了时刻 t t t的输出和时刻 t + 1 t+1 t+1的隐藏状态。所以,也影响了时刻 t + 1 t+1 t+1的输出和损失。因此,要评估 h t h_t ht累积的损失,我们需要知道它对当前输出以及后续输出的影响。
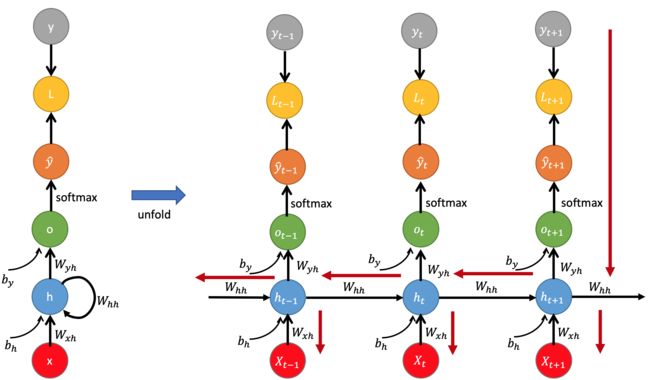
此时,需要修改反向传播算法,形成两阶段的算法来训练RNN中的权重。第一阶段,在第一次传播中,我们执行正向推理,如上图右边黑色箭头所代表的方向(从左到右),计算 h t , y t h_t,y_t ht,yt,在每个时刻累积损失,同时保存隐藏状态的值,以便在第二阶段使用。
在第二阶段,我们反向处理序列,从最后的输出往前计算梯度,即从右到左,如上图红色箭头所示。比如计算了 x t − 1 x_{t-1} xt−1处的梯度后,得到的损失还需要在前一步 x t x_t xt处使用。这种方法被称为沿着时间反向传播(Backpropagation Through Time,BPTT)。
我们说这里介绍的是Elman网络,那还有其他什么网络吗?
另一种称为Jordan网络。可以用以下公式来说明它们的区别:
Elman网络:
h t = g ( W h x t + U h h t − 1 + b h ) y t = f ( W y h t + b y ) \begin{aligned} h_t &= g(W_hx_t + U_hh_{t-1} + b_h) \\ y_t &= f(W_yh_t + b_y) \end{aligned} htyt=g(Whxt+Uhht−1+bh)=f(Wyht+by)
Jordan网络:
h t = g ( W h x t + U h y t − 1 + b h ) y t = f ( W y h t + b y ) \begin{aligned} h_t &= g(W_hx_t + U_hy_{t-1} + b_h) \\ y_t &= f(W_yh_t + b_y) \end{aligned} htyt=g(Whxt+Uhyt−1+bh)=f(Wyht+by)
其中 x t x_t xt为输入向量; h t h_t ht为隐藏状态; y t y_t yt为输出; W , U , b W,U,b W,U,b是参数; f f f和 g g g为激活函数。
RNN作为语言模型
RNN的这种特性,非常适用于语言模型。可以一次处理序列中的一个单词,基于当前的单词和上一个隐藏状态来预测下一个单词。可以看到,RNN没有N-Gram中N的限制,因为隐藏状态原则上可以表示前面所有单词的信息。
输入序列 X = [ x 1 ; ⋯ ; x t ; ⋯ ; x N ] X=[x_1;\cdots;x_t;\cdots;x_N] X=[x1;⋯;xt;⋯;xN]包含一系列大小为 ∣ V ∣ × 1 |V| \times 1 ∣V∣×1的独热向量,而输出 y y y是代表词典中所有单词概率分布的向量。在每个时刻中,模型通常使用嵌入矩阵 E E E来查看嵌入向量(而不是直接使用独热向量),然后与前一时刻的隐藏状态拼接来计算当前的隐藏状态。然后用于生成输出,它会喂给softmax层生成整个词典上的概率分布。即,在时刻 t t t:
由 V h t Vh_t Vht计算的向量可以看成是由 h t h_t ht提供的对整个词典的所有单词得分。将该得分传入sofmtax归一化后得到概率分布。某个单词 i i i作为下一个单词的概率由 y t [ i ] y_t[i] yt[i]表示,即 y t y_t yt的第 i i i个元素:
P ( w t + 1 = i ∣ w 1 , ⋯ , w t ) = y t [ i ] (6) P(w_{t+1}=i|w_1,\cdots,w_t) = y_t[i] \tag 6 P(wt+1=i∣w1,⋯,wt)=yt[i](6)
整个序列的概率就是序列中每个元素的概率之积,我们会使用 y i [ w i ] y_i[w_i] yi[wi]代表时刻 i i i的真实单词 w i w_i wi。那么,整个句子 w 1 : n w_{1:n} w1:n的概率就可以计算为:
P ( w 1 : n ) = ∏ i = 1 n P ( w i ∣ w 1 : i − 1 ) = ∏ i = 1 n y i [ w i ] (7) P(w_{1:n}) = \prod_{i=1}^n P(w_i|w_{1:i-1}) = \prod_{i=1}^n y_i[w_i] \tag 7 P(w1:n)=i=1∏nP(wi∣w1:i−1)=i=1∏nyi[wi](7)
为了训练一个RNN作为语言模型,我们使用文本语料作为训练材料,让模型在每个时刻 t t t预测下一个单词。然后训练模型最小化预测真正下一个单词的误差,使用交叉熵作为损失函数:
L C E = − ∑ w ∈ V y t [ w ] log y ^ t [ w ] (8) L_{CE} = - \sum_{w \in V} y_t[w]\log \hat y_t[w] \tag {8} LCE=−w∈V∑yt[w]logy^t[w](8)
在语言建模任务下,正确的分布 y t y_t yt来自于已知的下一个单词,通常被表示为独热向量,对应正确单词位置为 1 1 1,其他元素都为 0 0 0。这样,为语言建模的交叉熵损失由模型为正确单词赋予的概率决定。所以在时刻 t t t的损失就是模型赋予下个单词的负对数概率:
L C E ( y ^ t , y t ) = − log y ^ t [ w t + 1 ] (9) L_{CE}(\hat y_t,y_t) = -\log \hat y_t [w_{t+1}] \tag 9 LCE(y^t,yt)=−logy^t[wt+1](9)
因此,在输入的每个单词位置 t t t处,模型将正确的标记 w 1 : t w_{1:t} w1:t序列作为输入,并使用它们来计算可能的下一个单词的概率分布,从而计算下一个标记 w t + 1 w_{t+1} wt+1的模型损失。然后我们移动到下一个单词,此时我们忽略模型对下一个单词的预测,而是使用正确的标记 w 1 : t + 1 w_{1:t+1} w1:t+1的序列来估计标记 w t + 2 w_{t+2} wt+2的概率,这种方法被称为tearch forcing。
通过梯度下降来调整网络中的权值,以最小化训练序列上的平均交叉熵损失。上图说明了该训练过程。
可以发现,输入嵌入矩阵 E E E和最后一层权重矩阵 V V V(计算结果经过 softmax \text{softmax} softmax)很相似。 E E E的列向量代表在训练过程中学习到的词汇表中每个单词的词嵌入,目的是让具有相似含义和特征的单词具有相似的嵌入。并且,由于这些嵌入的长度对应于隐藏层 d h d_h dh的大小,因此嵌入矩阵 E E E的形状为 d h × ∣ V ∣ d_h×|V| dh×∣V∣。
最后一层矩阵 V V V提供了一种方法,通过计算 V h Vh Vh,对词典中每个单词的可能性进行评分。这得到了一个维度 ∣ V ∣ × d h |V|×d_h ∣V∣×dh。也就是说, V V V的行提供了第二组学习的词嵌入。这就引出了一个明显的问题——有必要同时拥有两者吗?权重绑定(weight tying)是一种避免这种权重冗余的方法,只需在输入和softmax层上使用同一组嵌入的方法。也就是说,我们在计算的开始和结束时都不用 V V V,而是使用 E E E。
这种改进,除了提升了模型困惑度之外,还显著减少了模型所需的参数量。
我们已经学习了RNN的基础知识,在实际应用上通常不是仅使用我们学到的这种RNN。而是会使用堆叠RNN和双向RNN。下面分别来了解它们。
堆叠RNN
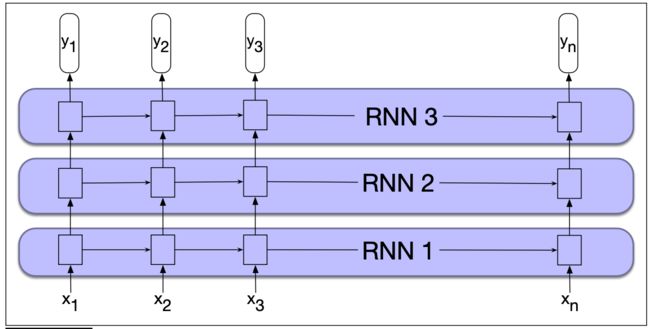
我们到此为止所学的例子中,RNN的输入都是由单词嵌入向量组成,而输出是预测单词有用的向量。但是,我们也可以使用一个RNN的整个输出作为另一个RNN的输入,通过这种方向将多个RNN网络堆叠起来。
如上图所示,我们堆叠了三个RNN。
堆叠的RNN通常优于单层RNN。可能的一个原因是,网络在不同层抽象了不同的表示。堆叠RNN的初始层产生的表示可以作为深层有用的抽象——这很难在单词RNN中产生。但是,随着堆叠层数的增加,训练成本也迅速上升。
双向RNN
另一种应用较多的是双向RNN,我们上面学到的是从左到右依次处理序列中的每个元素。但在很多情况下,如果能访问整个序列再做决定,得到的效果会更好。此时就需要双向RNN。
一种实现方式时通过两个独立的RNN网络,一个按照之前的顺序从左往右读;另一个按照逆序从右往左读。在每个时刻 t t t,拼接它们生成的表示。
References
- Speech and Language Processing