深度学习机器学习面试题——卷积与池化
深度学习机器学习面试题——卷积与池化
提示:
说说有哪些卷积
卷积实现原理?
卷积基本计算公式,padding
卷积操作后的特征图大小
常规卷积和深度可分离卷积的计算量
反卷积是怎么做的, unpooling中maxPooling怎么实现?
什么是空洞卷积?
知道哪些卷积类型?请介绍一下
为什么Depthwise卷积后还要进行pointwise卷积
卷积的底层实现/加速技巧
1x1卷积有什么作用
CNN有什么特点和优势
说说你了解的pooling方法
pooling层的作用
常用的pooling方法有哪些,那个更好?
说一下ROI Pooling
说一下maxpooling的反向传播怎么处理
语义分割上采样的方法
文章目录
- 深度学习机器学习面试题——卷积与池化
-
- @[TOC](文章目录)
- 说说有哪些卷积
- 什么是卷积?
- 上采样(Upsample)与反卷积(Transposed Convolution)
- Depthwise卷积与Pointwise卷积
- 分组卷积
- 卷积实现原理?用代码实现一下
- 卷积基本计算公式,padding
- 卷积操作后的特征图大小
- 常规卷积和深度可分离卷积的计算量
- 反卷积是怎么做的, unpooling中maxPooling怎么实现?
- 什么是空洞卷积?
- 知道哪些卷积类型?请介绍一下
- 为什么Depthwise卷积后还要进行pointwise卷积
- 卷积的底层实现/加速技巧
- 1x1卷积有什么作用
- CNN有什么特点和优势
- 说说你了解的pooling方法
- pooling层的作用
- 常用的pooling方法有哪些,那个更好?
- 说一下ROI Pooling
- 说一下maxpooling的反向传播怎么处理
- 语义分割上采样的方法
- 总结
文章目录
- 深度学习机器学习面试题——卷积与池化
-
- @[TOC](文章目录)
- 说说有哪些卷积
- 什么是卷积?
- 上采样(Upsample)与反卷积(Transposed Convolution)
- Depthwise卷积与Pointwise卷积
- 分组卷积
- 卷积实现原理?用代码实现一下
- 卷积基本计算公式,padding
- 卷积操作后的特征图大小
- 常规卷积和深度可分离卷积的计算量
- 反卷积是怎么做的, unpooling中maxPooling怎么实现?
- 什么是空洞卷积?
- 知道哪些卷积类型?请介绍一下
- 为什么Depthwise卷积后还要进行pointwise卷积
- 卷积的底层实现/加速技巧
- 1x1卷积有什么作用
- CNN有什么特点和优势
- 说说你了解的pooling方法
- pooling层的作用
- 常用的pooling方法有哪些,那个更好?
- 说一下ROI Pooling
- 说一下maxpooling的反向传播怎么处理
- 语义分割上采样的方法
- 总结
说说有哪些卷积
(1)标准卷积:标准卷积核与目标图像矩阵进行卷积运算,多少数量的卷积核,就会对应多少的特征图。【这是最经典的卷积】
(2)反卷积:反卷积是一种特殊的正向卷积,先按照一定的比例通过补0来扩大输入图像的尺寸,接着旋转卷积核(矩阵转置),再进行正向卷积。反卷积的操作只是恢复了矩阵X的尺寸大小,并不能恢复X的每个元素的原始值
(3)空洞卷积:空洞卷积或者膨胀卷积是在标准的卷积核里注入空洞,以此来增加感受野。相比原来的正常convolution,dilated convolution 多了一个超参数称之为 dilation rate(空洞率) 指的是kernel的间隔数量(e.g. 标准卷积的空洞率是1)。优点是在保持同等计算量的情况下可以扩大感受野,缺点是存在网格效应。
(4)深度可分离卷积:Depthwise Separable Convolution(深度可分离卷积)是将一个完整的卷积运算分解为两步运行,即Depthwise卷积 与 Pointwise卷积
Depthwise卷积不同于常规的操作,Depthwise convolution的一个卷积核只负责一个通道,即一个通道只被一个卷积核卷积。
Pointwise 卷积运算则是常规的运算,它的卷积核的尺寸为1x1xM,M为需要得到的最终feature map数量,所以这里的卷积运算会将上一步的map在深度方向上进行加权组合,生成新的feature map,总共为M维度,操作方法就是concate,然后再用1x1的卷积形成1维的map(也可以用1x1先卷积,然后将不同feature map进行add)。
(5)分组卷积:Group convolution 分组卷积,最早在AlexNet中出现,由于当时的硬件资源有限,训练AlexNet时卷积操作不能全部放在同一个GPU处理,因此作者把feature maps分给多个GPU分别进行处理,最后把多个GPU的结果进行融合。就是将特征图分成两半或几部分,卷积后再组合,组合方式一般是concate。
什么是卷积?
 在后面的图像处理中,都是离散处理,所以我们举个例子来理解一下卷积。
在后面的图像处理中,都是离散处理,所以我们举个例子来理解一下卷积。
比如我有两枚骰子,都投出去,问投掷出来的点数和为4的概率是多少?
这里问题的关键是,两个骰子加起来要等于4,这正是卷积的应用场景。
我们把骰子各个点数出现的概率表示出来:

那么,两枚骰子点数加起来为4的情况有:




图像中的卷积运算
有了上面的基础后,我们再来讲讲图像中的卷积运算,例子一个有噪点的原图,可以把它转为一个矩阵:
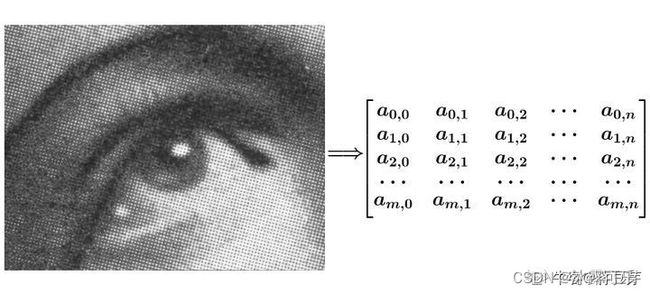
因为图像有噪点,我想平滑一下图像,
图像中的噪点属于高频信号,高频信号,就好像平地耸立的山峰,看起来很显眼。
平滑这座山峰的办法之一就是,把山峰刨掉一些土,填到山峰周围去。用数学的话来说,就是把山峰周围的高度平均一下。
用下面这个平均矩阵来平滑图像。
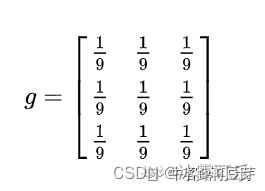
记得刚才说过的算法,把高频信号与周围的数值平均一下就可以平滑山峰。比如我要对点a1,1
进行卷积,那么我们从矩阵中取出a_{1,1}附近的点组成矩阵f,和g进行卷积运算后,再填回去。

要注意一点,f,虽然和g同维度,但下标有点不一样:

用一个动图来说明下计算过程:


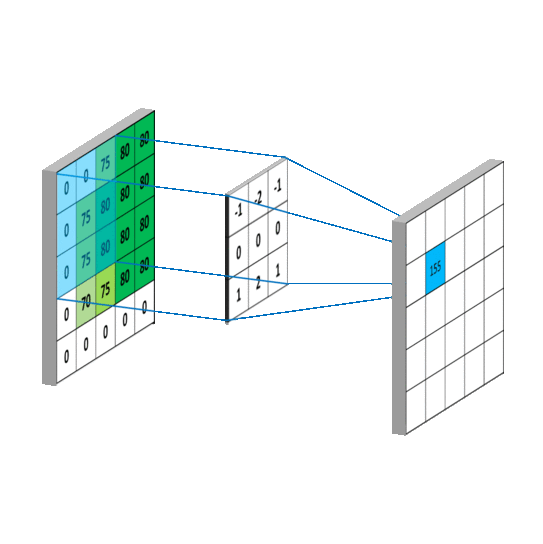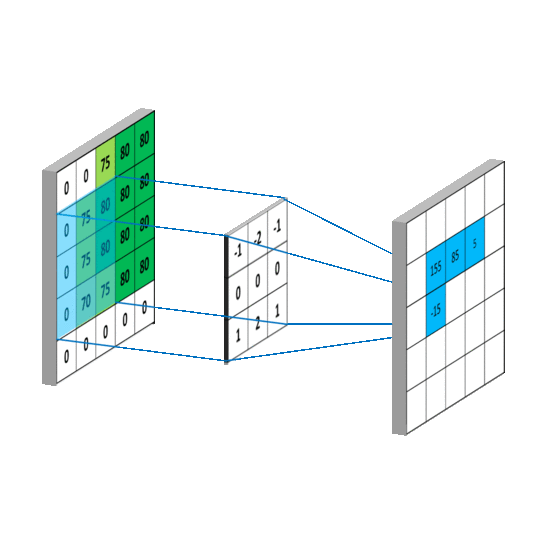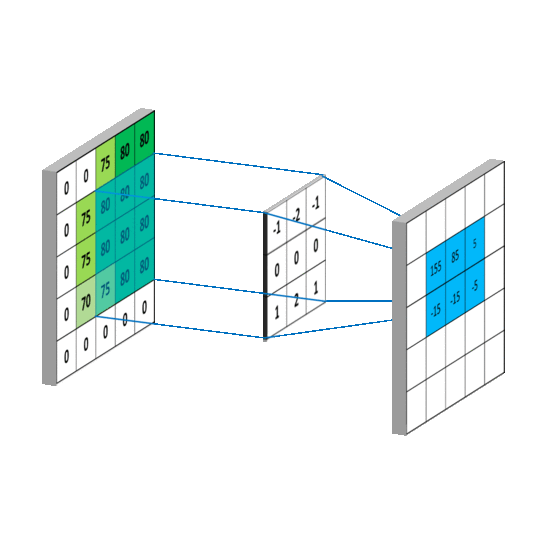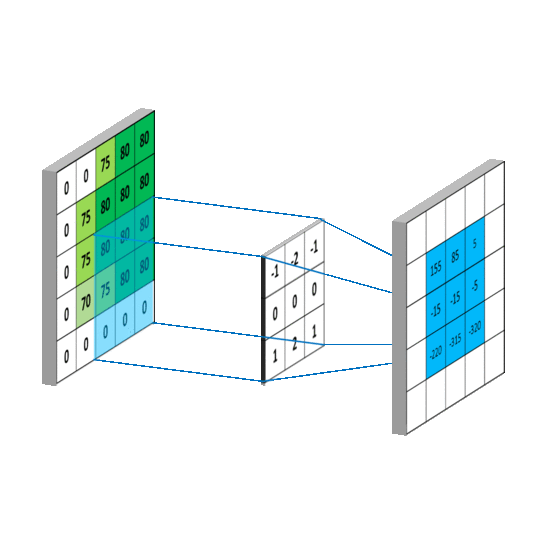
深度学习中的卷积层
卷积层(convolution layer)是卷积神经网络中的基础操作,作用是提取图像中的目标的特征。
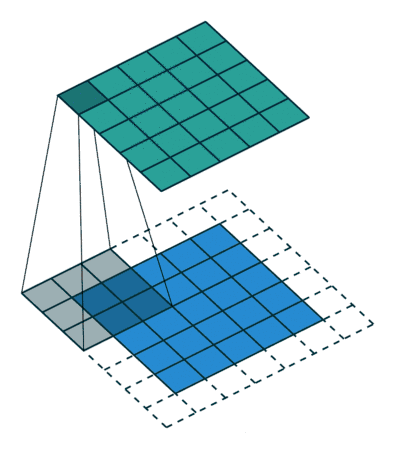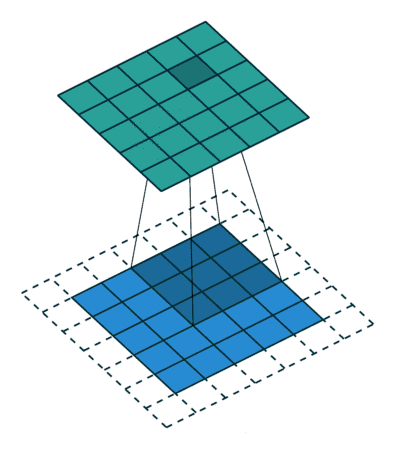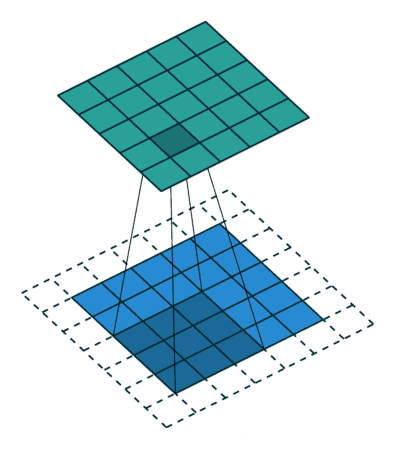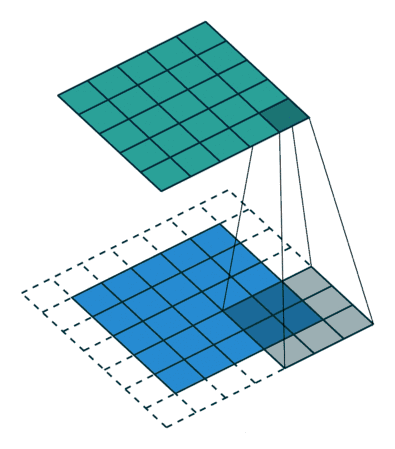
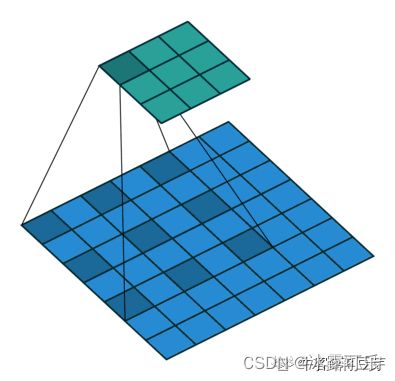
卷积时,卷积核滑动步长为1,从上图可以看出,一个5x5的矩阵经过3x3的卷积核后,生成的特征图为3x3。不过多数情况,为了保证特征图不变,我们会进行padding操作,padding操作是对目标矩阵的最外面一圈填充0,这样就保证生成的特征图大小和原矩阵一样大了。



权重共享
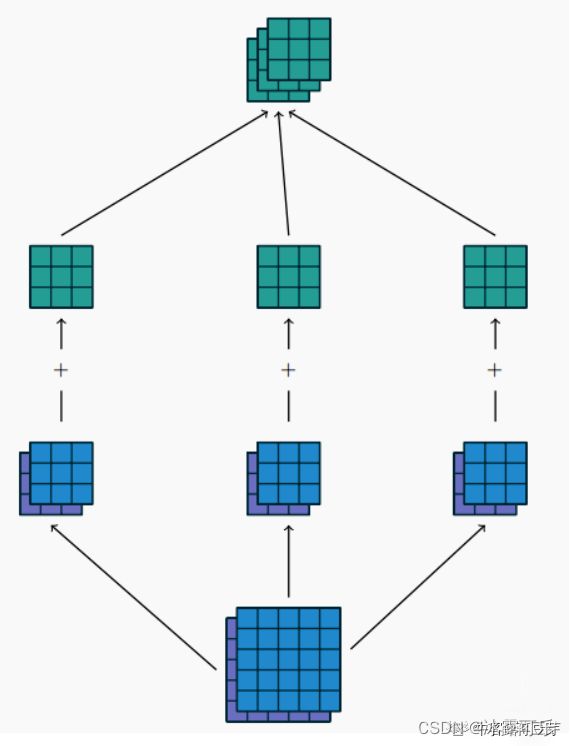
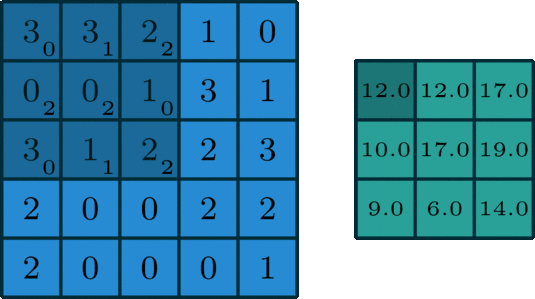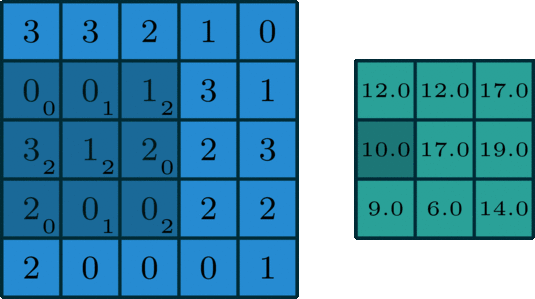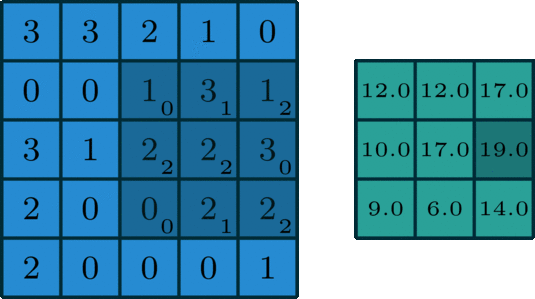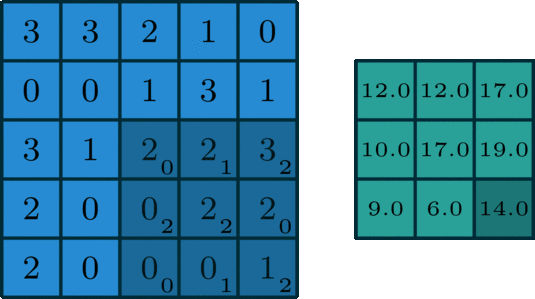
在卷积神经网络中,权重共享简单来理解就是,输入一张图片,这张图片用一个卷积核进行卷积操作的时候,图片中的每一个位置都被同一个卷积核进行卷积,所以权重是一样的,也就是共享。
深度学习中的卷积计算
卷积的计算是CNN中最基本的算术单元,卷积的计算过程中出现的:Input Feature Map(FP), Output Feature Map(FP), 以及与 Kernel(size, strides, padding, dilation rate等)之间的关系和计算方式是我们应该掌握的基本知识。
(1)卷积Input FP size 与 Output FP size之间的计算公式
如图1所示, 其展示了从Input FP 经过卷积计算得到 Output FP的过程,每个通道相互之间独立


这个公式,互联网大厂肯定会考的,比如京东的笔试题,选择题中就有让你计算尺寸的题目!!!
默认s=1
(2)池化操作输出特征图大小计算

(3)空洞卷积输出特征图大小计算

不给的参数统一为1
空洞卷积:Dilated/Atrous Convolution(中文叫做空洞卷积或者膨胀卷积) 或者是 Convolution with holes 从字面上就很好理解,是在标准的卷积核里注入空洞,以此来增加 感受野。相比原来的正常convolution,dilated convolution 多了一个超参数称之为 dilation rate(空洞率) 指的是kernel的间隔数量(e.g. 标准卷积的空洞率是1)。
对比标准卷积:
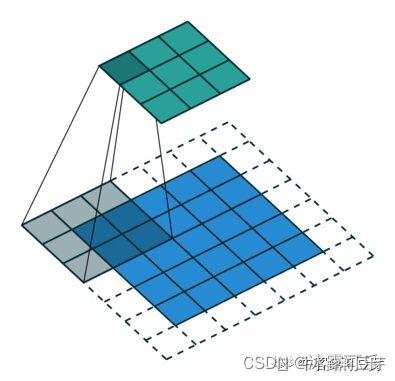
空洞卷积是这样的:
空洞卷积 Dilated Convolution with a 3 x 3 kernel and dilation rate d=2扩大了计算间隔(丢失局部像素信息)【可以扩大感受野】。
空洞卷积的优缺点:
优点是与标准卷积相比,在保持同等计算量的情况下,可以扩大感受野。对于检测与分割任务,扩大感受野可以提升精度;
缺点是会出现网格效应(gridding effect),丢失局部像素信息。
上采样(Upsample)与反卷积(Transposed Convolution)
在应用在计算机视觉的深度学习领域,由于输入图像通过卷积神经网络(CNN)提取特征后,输出的尺寸往往会变小,而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g. 图像的语义分割),这个采用扩大图像尺寸,实现图像由小分辨率到大分辨率的映射的操作,叫做上采样(Upsample)。
上采样有3种常见的方法:
双线性插值(bilinear),
反卷积(Transposed Convolution),
反池化(Unpooling),
我们这里只讨论反卷积。这里指的反卷积,也叫转置卷积,它并不是正向卷积的完全逆过程,用一句话来解释:反卷积是一种特殊的正向卷积,先按照一定的比例通过补0来扩大输入图像的尺寸,接着旋转卷积核,再进行正向卷积。
(1)正向卷积的实现过程

(2)用矩阵乘法描述反卷积

(3)双线性插值(bilinear)与反池化(Unpooling)
线性插值:双线性插值是目前在语义分割中用的比较多的一种方式,比如FCN中就是用的这种方法。双线性插值是高等数学里的知识,不再赘述。
**反池化(Unpooling):**在池化过程中,记录下max-pooling的max元素值在对应kernel中的坐标,在反池化过程中,根据之前的坐标将max元素填写回去,其他位置补0 。一句话总结就是,在下采样的时候记录max的位置,上采样的时候最大值的位置还原,其它位置填0,如下图所示:

双线性插值(bilinear)与反池化(Unpooling)的区别:通过一个图来说明:
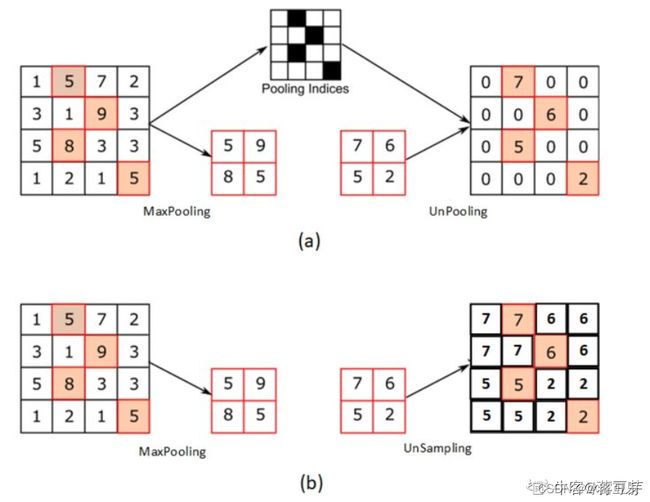
反池化的话,其余位置补0,但是双线性差值,整个max值全部补了
Depthwise卷积与Pointwise卷积
Depthwise卷积与Pointwise卷积,合起来被称作 Depthwise Separable Convolution(深度可分离卷积), 该结构和常规的卷积操作类似,可以用来提取特征,但相比于常规的卷积操作,其参数量和运算成本比较低,所以在一些轻量级网络中会碰到如此结构。
(1)咱们先看看常规卷积操作
对于一张5x5像素,三通道彩色输入图片,经过3x3x4卷积核的卷积层,最终会输出4个feature map。

此时,卷积层共4个Filter,每个Filter包含了3个Kernel,每个Kernel的大小为3×3。
(2)Depthwise Separable Convolution(深度可分离卷积)
Depthwise Separable Convolution(深度可分离卷积)是将一个完整的卷积运算分解为两步运行,即Depthwise卷积 与 Pointwise卷积
Depthwise卷积不同于常规的操作,Depthwise convolution的一个卷积核只负责一个通道,即一个通道只被一个卷积核卷积。
Pointwise 卷积运算则是常规的运算,它的卷积核的尺寸为1x1xM,M为需要得到的最终feature map数量,所以这里的卷积运算会将上一步的map在深度方向上进行加权组合,生成新的feature map,总共为M维度,操作方法就是concate,然后再用1x1的卷积形成1维的(也可以用1x1先卷积,然后将不同feature map进行add)。
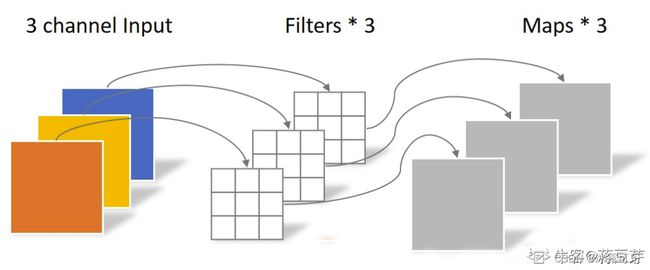
Depthwise Convolution完成后的Feature map数量与输入层的depth相同,但是这种运算对输入层的每个channel独立进行卷积运算后就结束了,没有有效的利用不同map在相同空间位置上的信息。因此需要增加另外一步操作来将这些map进行组合生成新的Feature map,即接下来的Pointwise Convolution。
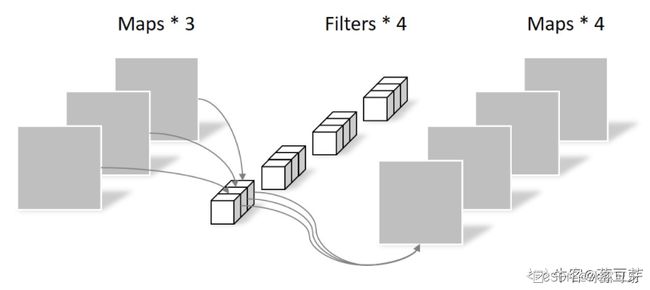
经过Pointwise Convolution之后,同样输出了4张Feature map,与常规卷积的输出维度相同。
(3)参数量计算
普通卷积:3x3x3x4=108
3x3是卷积核尺寸,3是输入图片通道数目,4是输出卷积核的个数。
深度可分离卷积:
DW:3x3x3x1=27
这里卷积核个数其实只设置为1。会形成3张feature map
PW:1x1x3x4=12
1x1为卷积核的尺寸,3为上一层feature map的数量,4为最终需要的维度。其实这里我们也得到了4维的feature map。
total: 27+12=39
明显可以看到,深度可分离卷积计算量比普通卷积小很多,只有其近三分之一的计算量。
分组卷积
Group convolution 分组卷积,最早在AlexNet中出现,由于当时的硬件资源有限,训练AlexNet时卷积操作不能全部放在同一个GPU处理,因此作者把feature maps分给多个GPU分别进行处理,最后把多个GPU的结果进行融合。下图就是将特征图分成两半,卷积后再组合。
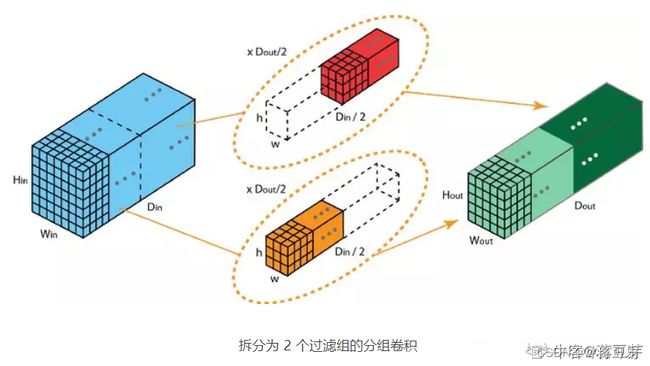
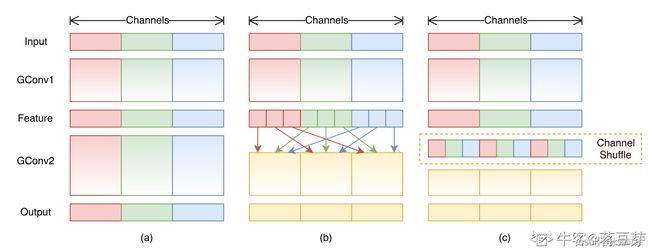
shuffleNet
pointwise卷积加强通道间的联系,还有另外的方式,那就是shuffleNet,shuffleNet通过将所有特征图通道“混洗”实现联系,思想比较简单,不再赘述。图C就体现了通道混洗的概念。
卷积实现原理?用代码实现一下
卷积是数学上的一种运算形式。
而神经网络中的卷积则是卷积运算的离散形式,是一种运算规则。
将卷积核旋转180°在原图上滑动卷积,从而生成特征图。
void im2col_cpu(float* data_im,
int channels, int height, int width,
int ksize, int stride, int pad, float* data_col) {
int c,h,w; //输入特征图转化得到的矩阵尺度 = (卷积组输入通道数*卷积核高*卷积核宽) * (卷积层输出单通道特征图高 * 卷积层输出单通道特征图宽)
int height_col = (height + 2*pad - ksize) / stride + 1; // 高度方向计算几次卷积
int width_col = (width + 2*pad - ksize) / stride + 1; // 宽度方向计算几次卷积
int channels_col = channels * ksize * ksize; // 输入矩阵展开//卷积核大小和通道数
for (c = 0; c < channels_col; ++c) { // 输出为:(输入通道*kh*kw)*卷积滑动的次数//多通道img2col的第一行
int w_offset = c % ksize; // 卷积核的索引 // 卷积核的宽度方向index
int h_offset = (c / ksize) % ksize; // 多通道img2col // 卷积核的高度方向index
int c_im = c / ksize / ksize; // 图像上的第index个通道 // 卷积核的通道方向的index
for (h = 0; h < height_col; ++h) { // 高度方向计算几次卷积 和卷积的计算方式,只是值相同,无任何相关意义
for (w = 0; w < width_col; ++w) { // 宽度方向计算几次卷积
int im_row = h_offset + h * stride; // 第几次卷积所需要的图像数据索引,行方向
int im_col = w_offset + w * stride; // 列方向
int col_index = (c * height_col + h) * width_col + w; // img2col之后,列项的索引
data_col[col_index] = im2col_get_pixel(data_im, height, width, channels,
im_row, im_col, c_im, pad);
}
}
}
}
卷积基本计算公式,padding
卷积操作后的特征图大小
常规卷积和深度可分离卷积的计算量
参数量计算
(1)普通卷积:3x3x3x 4 =108
3x3是卷积核尺寸,3是输入图片通道数目,4是输出卷积核的个数。
(2)深度可分离卷积:
DW:3x3x3x1=27
这里卷积核个数其实只设置为1。会形成3张feature map
PW:1x1x3x4=12
1x1为卷积核的尺寸,3为上一层feature map的数量,4为最终需要的维度。其实这里我们也得到了4维的feature map。
total: 27+12=39
明显可以看到,深度可分离卷积计算量比普通卷积小很多,只有其近三分之一的计算量。
反卷积是怎么做的, unpooling中maxPooling怎么实现?
反卷积,也叫转置卷积,它并不是正向卷积的完全逆过程,用一句话来解释:
反卷积是一种特殊的正向卷积**,先按照一定的比例通过补0来扩大输入图像的尺寸**,接着旋转卷积核,再进行正向卷积。
反池化(Unpooling):在池化过程中,记录下max-pooling的max元素值在对应kernel中的坐标,在反池化过程中,根据之前的坐标将max元素填写回去,其他位置补0 。
一句话总结就是,在下采样的时候记录max的位置,上采样的时候最大值的位置还原,其它位置填0
双线性差值,其余位置不是补零,而是全部都是max
什么是空洞卷积?
空洞卷积或者膨胀卷积是在标准的卷积核里注入空洞,以此来增加感受野。
相比原来的正常convolution,dilated convolution 多了一个超参数称之为 dilation rate(空洞率) 指的是kernel的间隔数量(e.g. 标准卷积的空洞率是1)。
优点是在保持同等计算量的情况下可以扩大感受野,
缺点是存在网格效应。丢失局部信息
知道哪些卷积类型?请介绍一下
(1)标准卷积,
标准卷积核与目标图像矩阵进行卷积运算,多少数量的卷积核,就会对应多少的特征图。
(2)反卷积
反卷积是一种特殊的正向卷积,先按照一定的比例通过补0来扩大输入图像的尺寸,接着旋转卷积核(矩阵转置),再进行正向卷积。反卷积的操作只是恢复了矩阵 X的尺寸大小,并不能恢复X的每个元素的原始值
(3)空洞卷积
空洞卷积或者膨胀卷积是在标准的卷积核里注入空洞,以此来增加感受野。相比原来的正常convolution,dilated convolution 多了一个超参数称之为 dilation rate(空洞率) 指的是kernel的间隔数量(e.g. 标准卷积的空洞率是1)。优点是在保持同等计算量的情况下可以扩大感受野,缺点是存在网格效应。
(4)深度可分离卷积
Depthwise Separable Convolution(深度可分离卷积)是将一个完整的卷积运算分解为两步运行,即Depthwise卷积 与 Pointwise卷积
Depthwise卷积不同于常规的操作,Depthwise convolution的一个卷积核只负责一个通道,即一个通道只被一个卷积核卷积。
Pointwise 卷积运算则是常规的运算,它的卷积核的尺寸为1x1xM,M为需要得到的最终feature map数量,所以这里的卷积运算会将上一步的map在深度方向上进行加权组合,生成新的feature map,总共为M维度,操作方法就是concate,然后再用1x1的卷积形成1维的map(也可以用1x1先卷积,然后将不同feature map进行add)。【1/3的计算量】
(4)分组卷积
Group convolution 分组卷积,最早在AlexNet中出现,由于当时的硬件资源有限,训练AlexNet时卷积操作不能全部放在同一个GPU处理,因此作者把feature maps分给多个GPU分别进行处理,最后把多个GPU的结果进行融合。就是将特征图分成两半或几部分,卷积后再组合,组合方式一般是concate。
为什么Depthwise卷积后还要进行pointwise卷积
Depthwise Convolution完成后的Feature map数量与输入层的depth相同,
但是这种运算对输入层的每个channel独立进行卷积运算后就结束了,
没有有效的利用不同map在相同空间位置上的信息。
因此需要增加另外一步操作来将这些map进行组合生成新的Feature map,即接下来的Pointwise Convolution。
卷积的底层实现/加速技巧
卷积在图像处理中,可通过矩阵相乘来实现。
所以可以从矩阵运算入手来加速。主要方式是低秩近似算法。
(1)使用结构化矩阵近似重构原矩阵。
(2)使用SVD矩阵分解方法来重构矩阵。
1x1卷积有什么作用
(1)实现跨通道的交互和信息整合
(2)进行卷积核通道数的降维和升维
(3)对于单通道feature map 用单核卷积即为乘以一个参数,而一般情况都是多核卷积多通道,实现多个feature map的线性组合
(4)可以实现与全连接层等价的效果。如在faster-rcnn中用1x1xm的卷积核卷积n(如512)个特征图的每一个位置(像素点),其实对于每一个位置的1x1卷积本质上都是对该位置上n个通道组成的n维vector的全连接操作。
CNN有什么特点和优势
CNN的使用范围是具有局部空间相关性的数据,比如图像、自然语言、语音。
(1)局部连接(稀疏连接):可以提取局部特征
(2)权值共享:减少参数数量,降低训练难度,避免过拟合,提升模型“平移不变性”
(3)降维:通过池化或卷积stride实现
(4)多层次结构:将低层次的局部特征组合成较高层次的特征,不同层级的特征可以对应不同任务【low-level和high-level】
说说你了解的pooling方法
(1)平均池化(average pooling):计算图像区域的平均值作为该区域池化后的值。
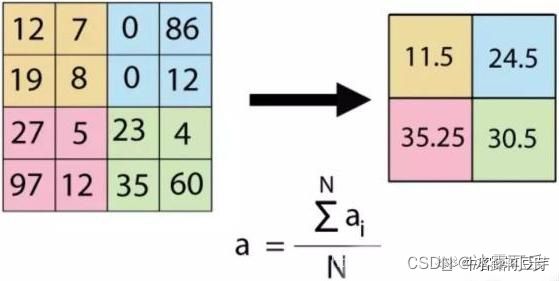
(2)最大池化(max pooling):选图像区域的最大值作为该区域池化后的值。

(3)Stochastic pooling(随机池化)
Stochastic pooling是一种简单有效的正则化CNN的方法,能够降低max pooling的过拟合现象,提高泛化能力。
对于pooling层的输入,根据输入的多项式分布随机选择一个值作为输出。训练阶段和测试阶段的操作略有不同。
训练阶段:
1)前向传播:先将池化窗口中的元素全部除以它们的和,得到概率矩阵;再按照概率随机选中的方格的值,作为该区域池化后的值。(stochastic pooling方法非常简单,只需对feature map中的元素按照其概率值大小随机选择,即元素值大的被选中的概率也大。而不像max-pooling那样,永远只取那个最大值元素。)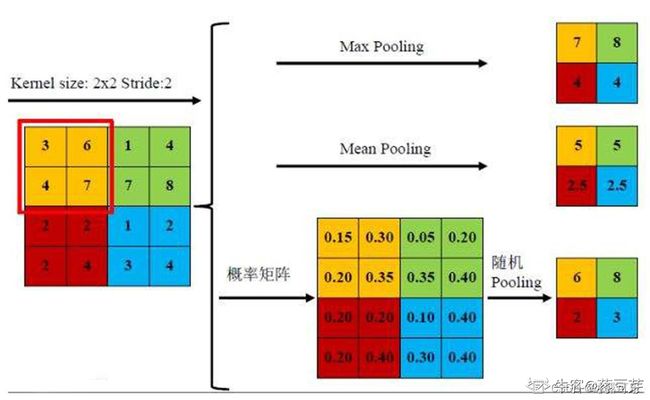
反向传播:求导时,只需保留前向传播中已经被选中节点的位置的值,其它值都为0,类似max-pooling的反向传播。
测试阶段:
在测试时也使用Stochastic Pooling会对预测值引入噪音,降低性能。取而代之的是使用概率矩阵加权平均。比使用Average Pooling表现要好一些。在平均意义上,与Average Pooling近似,在局部意义上,服从Max Pooling准则。
(4)重叠池化就是,相邻池化窗口之间有重叠区域,此时一般sizeX > stride。
(5)步长为2的卷积【空洞卷积呗】
(6)空间金字塔池化SPP(Spatial Pyramid Pooling):使得我们构建的网络,可以输入任意大小的图片,不需要经过裁剪缩放等操作,只要你喜欢,任意大小的图片都可以。不仅如此,这个算法用了以后,精度也会有所提高。
在之前的CNN中,对于结构已经确定的网络,需要输入一张固定大小的图片,比如224x224、32x32、96x96等。这样对于我们希望检测各种大小的图片的时候,需要经过裁剪,或者缩放等一系列操作,这样往往会降低识别检测的精度。
空间金字塔池化SPP使得我们构建的网络,可以输入任意大小的图片,不需要经过裁剪缩放等操作,只要你喜欢,任意大小的图片都可以。不仅如此,这个算法用了以后,精度也会有所提高。
R-CNN是直接从原始图片中提取特征,它在每张原始图片上提取2000个Region Proposal,然后对每一个候选区域框缩放到227x227进行一次卷积计算,差不多要重复2000次,利用SVM算法进行分类识别。
而SPP-net则是在卷积原始图像之后的特征图上提取候选区域的特征。所有的卷积计算只进行了一次,效率大大提高。
目的:解决不管输入图片的大小是多大,都可以用当前的网络进行测试的问题。
还能避免cropping和warping操作,导致一些信息的丢失,具有非常重要的意义。
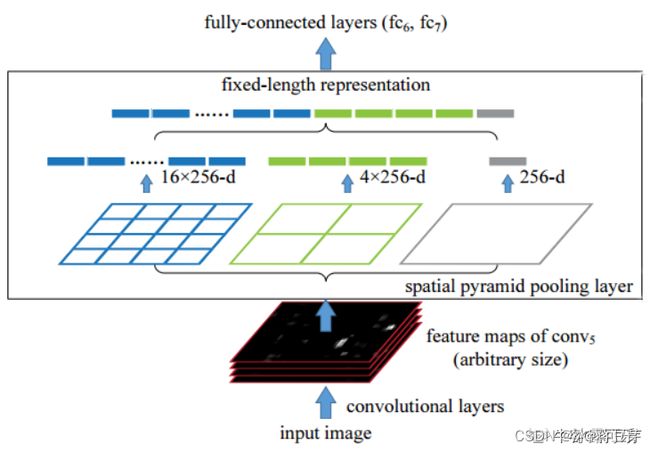
空间金字塔池化SPP原理: 如上图所示,从下往上看,这是一个传统的网络架构模型,5层卷积层,这里的卷积层叫做convolution和pooling层的联合体,统一叫做卷积层,后面跟随全连接层。我们这里需要处理的就是在网络的全连接层前面加一层金字塔pooling层解决输入图片大小不一的情况。注意我们上面曾提到使用多个窗口(不同尺寸的pooling窗口,如上图中蓝色,青绿,银灰的窗口, 然后对feature maps 进行pooling,将分别得到的结果进行合并就会得到固定长度的输出), 这就是得到固定输出的秘密原因。这就解决了特征图大小不一的状况了。文章中用的是AlexNet,conv5得到的feature map大小为13x13x256。SPP其实就是做了多尺度的提取特征。


(7)ROI Pooling–SSP的改进版本
ROI pooling具体操作如下:
1)根据输入image,将ROI映射到feature map对应位置;
2)将映射后的区域划分为相同大小的sections(sections数量与输出的维度相同);
3)对每个sections进行max pooling操作;
这样我们就可以从不同大小的方框得到固定大小的相应 的feature maps。值得一提的是,输出的feature maps的大小不取决于ROI和卷积feature maps大小。ROI pooling 最大的好处就在于极大地提高了处理速度。ROI pooling 其实就是SSP演化,SSP是对整个feature maps划分区域然后pooling;而ROI pooling 则是对ROI划分区域然后pooling。
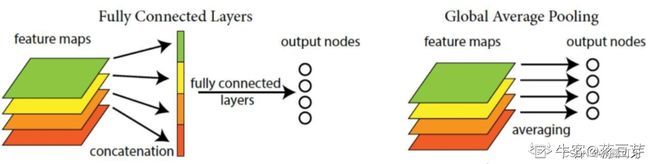
(8)全局平均池化层GAP:是一种代替全连接层的思路。全连接层进行了信息的转化,卷积层进行信息的提取,而池化更多的是信息的压缩。但单靠全局平均池化确实不能替代卷积层,还需要配合若干层卷积层,对信息进行提取和转化,最终整形到期望输出的维度,再通过全局平均池化完成输出。

pooling层的作用
池化的作用体现在降采样:保留显著特征、降低特征维度,提升网络不变性。通过池化整合特征,网络提取的特征图越来越接近我们的目标。



从CNN的特征提取可视化来看,一开始网络提取的是边缘特征,然后到局部特征,最后整合成了完整的目标特征。池化从中发挥了重要作用,描述了图像的高层抽象。
pooling主要是三个作用:
(1)invariance(不变性),这种不变性包括translation(平移),rotation(旋转),scale(尺度)
(2)保留主要的特征同时减少参数(降维,效果类似PCA)和计算量,防止过拟合,提高模型泛化能力
(3)减少计算量
pooling是在卷积网络(CNN)中一般在卷积层(conv)之后使用的特征提取层,使用pooling技术将卷积层后得到的小邻域内的特征点整合得到新的特征。一方面防止无用参数增加时间复杂度,一方面增加了特征的整合度。
pooling是用更高层的抽象表示图像特征,至于pooling为什么可以这样做,是因为:我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计。这个均值或者最大值就是一种聚合统计的方法。
做窗口滑动卷积的时候,卷积值就代表了整个窗口的特征。因为滑动的窗口间有大量重叠区域,出来的卷积值有冗余,进行最大pooling或者平均pooling就是减少冗余。减少冗余的同时,pooling也丢掉了局部位置信息,所以局部有微小形变,结果也是一样的。就像图片上的字母A,局部出现微小变化,也能够被识别成A。而加上椒盐噪音,就是字母A上有很多小洞,同样的能够被识别出来。而平移不变性,就是一个特征,无论出现在图片的那个位置,都会识别出来。所以平移不变性不是pooling带来的,而是层层的权重共享带来的。
常用的pooling方法有哪些,那个更好?
最常用的有三种
平均池化(average pooling):计算图像区域的平均值作为该区域池化后的值。
最大池化(max pooling):选图像区域的最大值作为该区域池化后的值。
Stochastic pooling(随机池化)
根据相关理论,特征提取的误差主要来自两个方面:
(1)邻域大小受限造成的估计值方差增大;
(2)卷积层参数误差造成估计均值的偏移。
一般来说,mean-pooling能减小第一种误差,更多的保留图像的背景信息,max-pooling能减小第二种误差,更多的保留纹理信息。
Stochastic-pooling则介于两者之间,通过对像素点按照数值大小赋予概率,再按照概率进行亚采样,在平均意义上,与mean-pooling近似,在局部意义上,则服从max-pooling的准则。
Stochastic-pooling更好。
其他池化方法
(4)重叠池化就是,相邻池化窗口之间有重叠区域,此时一般sizeX > stride。
(5)步长为2的卷积
(6)空间金字塔池化SPP(Spatial Pyramid Pooling):使得我们构建的网络,可以输入任意大小的图片,不需要经过裁剪缩放等操作,只要你喜欢,任意大小的图片都可以。不仅如此,这个算法用了以后,精度也会有所提高。
(7)ROI Pooling
(8)全局平均池化层GAP:是一种代替全连接层的思路。全连接层进行了信息的转化,卷积层进行信息的提取,而池化更多的是信息的压缩。但单靠全局平均池化确实不能替代卷积层,还需要配合若干层卷积层,对信息进行提取和转化,最终整形到期望输出的维度,再通过全局平均池化完成输出。
说一下ROI Pooling
RoIPooling顾名思义对Roi进行Pooling操作,主要用于目标检测任务。
RoI(Region of interest)指的是一张图片中认为有存在目标的区域,RoI大小不一。RoIPooling的特性是输入特征图的大小不确定,输出的特征图的大小固定。
ROI pooling 其实就是SSP演化,SSP是对整个feature maps划分区域然后pooling;而ROI pooling 则是对ROI划分区域然后pooling。
ROI pooling具体操作如下:
1)根据输入image,将ROI映射到feature map对应位置;
2)将映射后的区域划分为相同大小的sections(sections数量与输出的维度相同);
3)对每个sections进行max pooling操作;
这样我们就可以从不同大小的方框得到固定大小的相应 的feature maps。值得一提的是,输出的feature maps的大小不取决于ROI和卷积feature maps大小。
ROI pooling 最大的好处就在于极大地提高了处理速度。
说一下maxpooling的反向传播怎么处理
maxpooling:求导时,只需保留前向传播中已经被选中节点的位置的值,其它值都为0。
平均池化:在反向传播时,需要将值平均分配给每一个神经元再进行反向传播
池化层在反向传播时**,它是不可导的**,因为它是对特征图进行下采样会导致特征图变小,比如一个2x2的池化,在L+1层输出的特征图是16个神经元,那么对应L层就会有64个神经元,两层之间经过池化操作后,特征图尺寸改变,无法一一对应,这使得梯度无法按位传播。那么如何解决池化层不可导但却要参与反向传播呢?
在反向传播时,梯度是按位传播的,那么,一个解决方法,就是如何构造按位的问题,但一定要遵守传播梯度总和保持不变的原则。
对于平均池化,其前向传播是取某特征区域的平均值进行输出,这个区域的每一个神经元都是有参与前向传播了的,因此,在反向传播时,框架需要将梯度平均分配给每一个神经元再进行反向传播,相关的操作示意如下图所示。
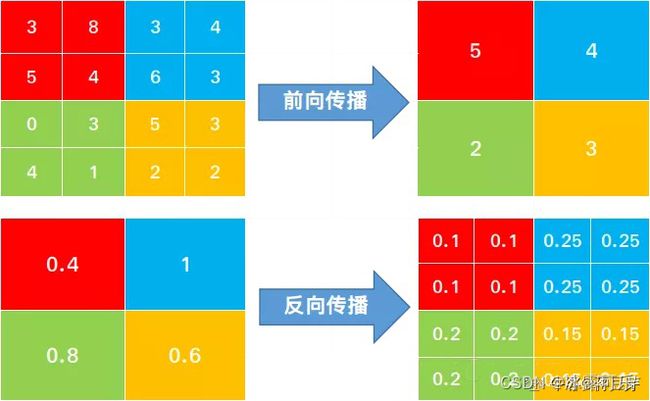
对于最大池化,其前向传播是取某特征区域的最大值进行输出,这个区域仅有最大值神经元参与了前向传播,因此,在反向传播时,框架仅需要将该区域的梯度直接分配到最大值神经元即可,其他神经元的梯度被分配为0且是被舍弃不参与反向传播的,但如何确认最大值神经元,这个还得框架在进行前向传播时记录下最大值神经元的Max ID位置,这是最大池化与平均池化差异的地方,相关的操作示意如下图所示。

其中,上述表格中,前向传播时,每个单元格表示特征图神经元值,而在反向传播时,每个单元格表示的是分配给对应神经元的梯度值。
语义分割上采样的方法
上采样有3种常见的方法:
双线性插值(bilinear),
反卷积(Transposed Convolution),
反池化(Unpooling)
总结
提示:重要经验:
1)深度学习和机器学习在互联网大厂中的笔试,或者面试都会遇到的知识点
2)没事来看看,总会有用的
3)笔试求AC,可以不考虑空间复杂度,但是面试既要考虑时间复杂度最优,也要考虑空间复杂度最优。

